Best Of
Question
Bonjour cher équipe Allo prof j'ai biento un évaluation de français sur les classe de mot je suis en sec 1 et j'ai beaucoup de difficulté avec les 3 invariable pouvez vous m'aider svp
Re: Question
Bonjour,
Tu dois factoriser premièrement le numérateur. Par la suite, tu devras factorisé le dénominateur.
Une fois cela fait, tu peux simplifier les termes en commun entre ton numérateur et ton dénominateur.
Voici un lien utile :
Bonne journée
Re: Question
Salut!
Tout d'abord, ta réponse au numéro a est la bonne, bravo! :D
Cependant, je te conseille de réduire tes fractions pour t'aider au fil de tes calculs. Par exemple, 140/20 est égal à 7. Tu aurais donc pu faire 7,5-5, ce qui t'aurai enlevé l'étape de transformer 7,5 en une fraction dont le dénominateur est 20.
De plus, ta réponse finale est 10/20, mais tu peux réduire cette fraction et écrire 1/2. Encore mieux, étant donné qu'on parle ici de kg, il est préférable de donner ta réponse en nombre décimal : elles doivent couper 0,5 kg de poireau.
Ensuite, pour le numéro b), on veut savoir si les deux amies peuvent se séparer également la masse des légumes. En d'autres mots, puisqu'il y a un total de 7,5 kg de légumes, on veut que chacune ait la moitié, soit 3,75 kg.
Donc, il faut que la moitié de la masse totale soit possible avec certaines combinaisons de sacs.
Les masses de chaque sac sont :
- Carottes : 1,75 kg
- Céleri : 0,75 kg
- Oignons : 1,9 kg
- Patates douces : 2,6 kg
- Poireaux : 0,5 kg
On doit chercher deux ensembles de sacs qui donnent 3,75 kg exactement. Par exemple :
- Corinne : Carottes + Céleri + Poireaux = 1,75 + 0,75 + 0,5 = 3 kg
- Anne : Oignons + Patates douces = 1,9 + 2,6 = 4,5 kg
Cette combinaison ne fonctionne pas, puisqu'Anne en possède plus que Corinne.
Si tu ne trouves aucune combinaison de sacs qui donne exactement 3,75 kg, alors cela signifie qu'elles ne peuvent pas se séparer également la masse des légumes sans mélanger les sacs.
J'espère que cela t'aide! :)
Re: Question
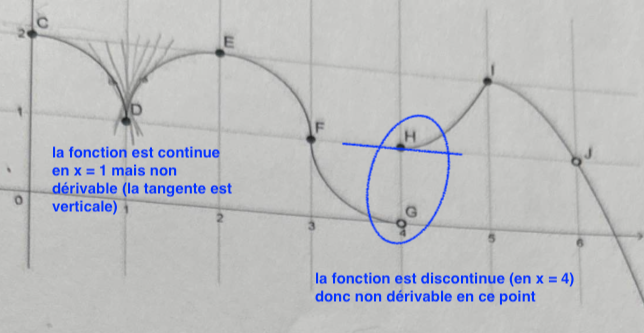
En x = 1 la tangente est verticale (pente infinie), la dérivée n'existe pas, elle n'a pas de valeur réelle.
En x = 4 la fonction est discontinue elle n'est donc pas dérivable
Si on t'avait donné la fonction valeur absolue, la fonction ne serait pas dérivable au sommet (qui forme un coin) car la dérivée à droite serait différente de la dérivée à gauche en ce point.
Re: Question
Bonjour TatouInsolite630,
Merci d’utiliser la zone d'entraide :) Je vais te guider.
Quand on voit (x + 1)², ça veut dire (x + 1) × (x + 1).
Donc, on doit multiplier chaque terme :
- x × x = x² → c’est pour ça que le x a un exposant 2.
- x × 1 = x et 1 × x = x → si on les additionne, ça donne 2x.
- 1 × 1 = 1 → c’est le dernier terme.
Alors au final,
(x + 1)² = x² + 2x + 1
Pour t’aider je te laisse une fiche explicative:
Ne lâche pas! Et n’hésite pas à revenir nous voir si tu as des questions :)
CigogneNoble4278
Re: Question
Bonjour,
Développons cela ensemble.
\(-3x * (x-2) - 4(x+1)^2 \)
Dans cette expression, tu as deux composantes :
1) \(-3x * (x-2)\)
2) \(- 4(x+1)^2 \)
Premièrement, tu peux développer la composante (1), comme cela :
\(-3x * (x-2) =\)
\(-3x * x - -3x*2 =\)
\(-3x^2 + 6x\)
Deuxièmement, tu peux développer la composante (2), comme cela :
\(- 4(x+1)^2 =\)
\(- 4(x+1) * (x+1) =\)
\(-4 * [(x+1) * (x+1)]=)\)
\(-4 * [x^2 + x + x + 1]=)\)
\(-4 * [x^2 + 2x + 1])\)
Donc, en regroupant nos deux composantes, nous obtenons :
\(-3x^2 + 6x -4 * [x^2 + 2x + 1])\)
Voici un lien utile :
Si tu as d'autres questions, n'hésite pas à venir les poser !
Bonne journée :)
Re: Question
Bonjour,
Je ne pense pas que tu as lu mon explication, donc je te redonne le lien :
Si tu as des questions après avoir lu mon explication, dis-nous ce que tu ne comprends pas exactement et nous serons heureux de t'aider.
Bonne journée :)
Re: Question
Bonjour,
Merci d’utiliser la Zone d’entraide!!
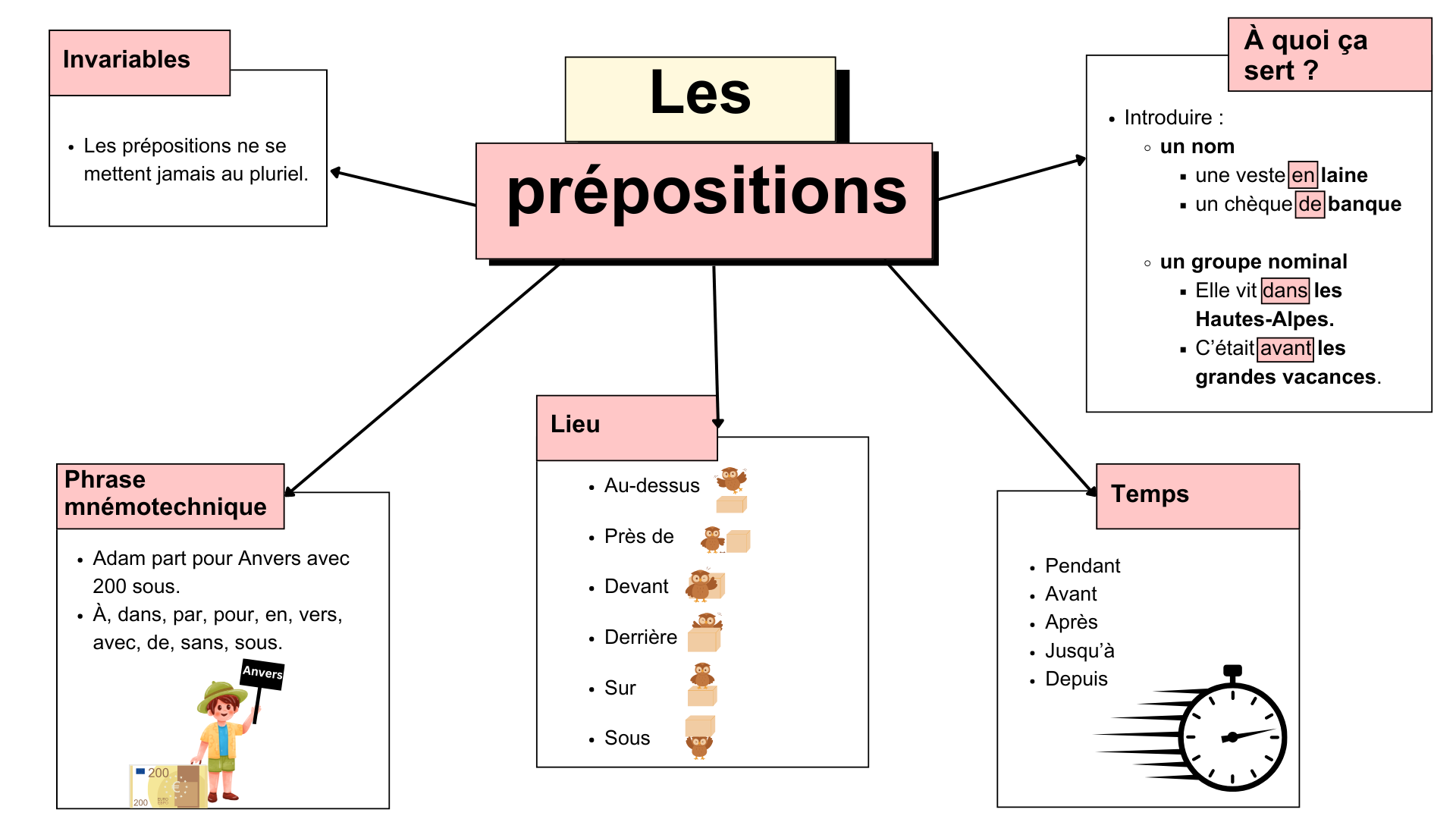
Je vais t’expliquer comment distinguer un adverbe d’une préposition.
Définition simple
- Un adverbe complète ou modifie un verbe, un adjectif ou un autre adverbe.
- ➜ Il n’est pas suivi d’un nom.
- Une préposition relie deux mots (souvent un verbe et un nom).
- ➜ Elle est toujours suivie d’un nom, d’un pronom ou d’un verbe à l’infinitif.
Exemples
Adverbes :
- Il marche vite.
- Elle habite loin.
- Il est très gentil.
- Viens ici.
Prépositions :
- Il marche dans la rue.
- Elle habite loin de la ville.
- Il parle avec ses amis.
- Je vais à l’école.
Truc à retenir :
- Pas de mot après = adverbe
- Nom, pronom ou verbe après = préposition
Tu peux consulter ces fiches Alloprof pour t’exercer :
Ne lâche pas!!!
N’hésite pas à revenir si tu as d’autres questions.
KiwiCocasse8992
Re: Question
Bonjour, NeptuneAlpha3795! :D
Merci pour ta question.
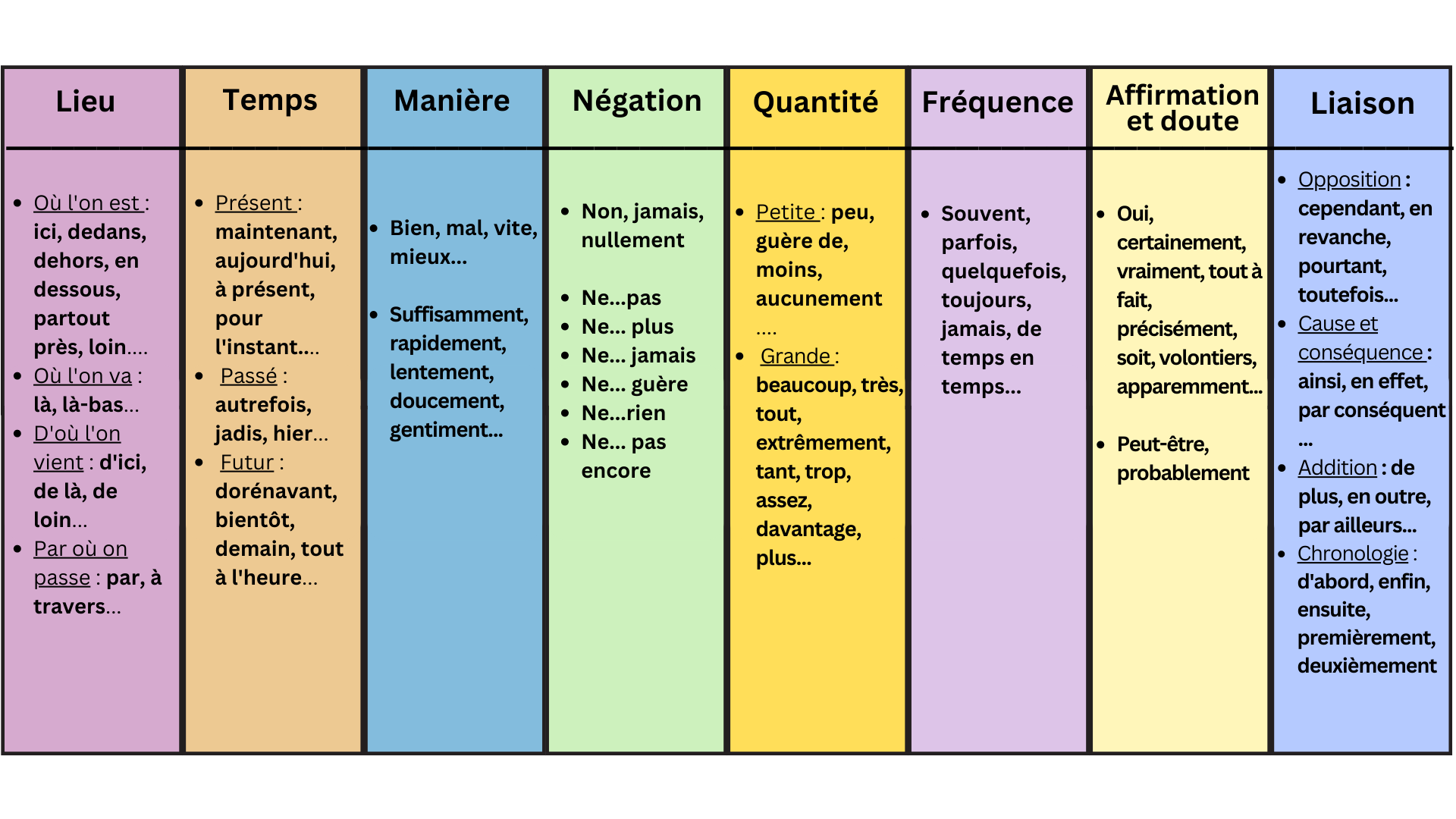
Les adverbes et les prépositions sont tous les deux des mots invariables, c'est-à-dire qui s'écrivent toujours de la même manière.
Premièrement, l'adverbe sert à modifier, préciser ou apporter une nuance de sens à un verbe, à un adjectif ou à un autre adverbe.
Ils peuvent avoir différents sens : voici des exemples.
Voilà notre fiche sur l'adverbe:
Une préposition sert à introduire un complément et à relier ce complément au reste de la phrase. Elle ne peut jamais être utilisée seule, contrairement à l'adverbe.
Voici des exemples:
La préposition établit une relation (temps, lieu, cause, etc.) entre le complément et le mot qu'elle précède (verbe, nom ou adjectif).
Voici notre fiche sur la préposition :
La façon la plus simple de différencier un adverbe d'une préposition est de vérifier si le mot est suivi d'un complément. Pour le savoir, tu peux te poser cette question :
« Est-ce que le mot relie ce qui vient après à ce qui vient avant? »
Si c'est le cas, c'est parce que c'est une préposition. Ça ne fonctionne pas avec l'adverbe, car il se suffit à lui-même. Il modifie le verbe ou l'adjectif sans nécessiter de mot pour compléter son sens. S'il y a des mots qui suivent, ils ne sont pas liés à l'adverbe directement.
J'espère avoir répondu à ta question. N'hésite pas à nous réécrire si tu en as d'autres! :)
Iris
Re: Question
Merci pour ta question!
La réflexion diffuse intervient sur les surfaces irrégulières (ou non polies). La lumière est réfléchie dans plusieurs directions.
La réflexion spéculaire est une réflexion régulière de la lumière. Contrairement à la réflexion diffuse, elle ne peut exister que si les rayons lumineux rencontrent une surface parfaitement plane ou polie.
Le site d'Alloprof n'a pas d'exercice sur la réflexion spéculaire et diffuse. Par contre, tu peux toi-même te promener dans ton environnement et identifier des exemples de réflexion diffuse et spéculaire.
En effet, si un objet reflète la lumière sans qu'on puisse y distinguer une image nette et précise, il s'agit de réflexion diffuse. Si un objet reflète la lumière et qu'on peut y distinguer une image nette et précise, il s'agit de réflexion spéculaire.
Cette fiche du site d'Alloprof explique la réflexion :
N'hésite pas si tu as d'autres questions!