Best Of
Question
Bonjour, j'ai essayé de comprendre le concept d'optimisation, mais j'ai encore des diffcultés, j'ai fais des exercices, lu les fiches alloprof, lu mes notes de cours, regarder la mini récup d'alloprof sur se sujet etc. Comment expliqueriez vous d'une façon assez simple c'est quoi l'optimisation.
Re: Question
Merci pour ta question!
La constante d'acidité et de basicité sont tous deux des méthodes pour mesurer la solubilité d'un acide ou d'une base, et donc, une mesure indirecte de leur puissance.
Les deux constantes ont des formules très similaires :
$$ K_a = \frac{[H^+][A^-]}{[HA]} $$
Légende :
• Ka : constante d'acidité
• [H+] : concentration de H+ (mol/L)
• [A-] : concentration de la base conjuguée (mol/L)
• [HA] : concentration de l'acide non dissocié (mol/L)
$$ K_b = \frac{[B^+][OH^-]}{[B]} $$
Légende :
• Kb : constante de basicité
• [B+] : concentration de l'acide conjugué (mol/L)
• [OH-] : concentration de OH- (mol/L)
• [B] : concentration de la base non dissociée (mol/L)
Par contre, les deux mesures sont différentes. La constante d'acidité est utilisée pour trouver la force d'un acide. La constante de basicité est utilisée pour trouver la force d'une base. Dans les deux cas, plus la constante est élevée, plus la solution est forte.
En théorie, on pourrait utiliser la constante d'acidité ou de basicité pour mesurer des bases ou des acides, respectivement, mais cela ne serait pas pratique. Rappelle toi qu'on peut aisément convertir la constante d'acidité en constante de basicité et vice versa grâce à la formule suivante :
$$ K_a•K_b = K_{eau} = 10^{-14} $$
À propos de la constante d'ionisation de l'eau, celle-ci représente la capacité de l'eau à s'auto-ioniser. Cela correspond au produit de la concentration de H+ et de OH- et est équivalent à 10^-14 :
$$ K_{eau} = [H^+][OH^-] = 10^{-14} $$
La constante du produit de solubilité mesure la solubilité d'un ion peu soluble dans l'eau :
$$ K_{ps}=[X^+]^n[Y^-]^m $$
Légende :
• Kps : constante du produit de solubilité
• [X] : concentration de l'ion X
• n : coefficient de l'ion dans la réaction de dissolution
• [Y] : concentration de l'ion Y
• m : coefficient de l'ion dans la réaction de dissolution
Plus la constante est élevée, plus la substance se dissout bien dans l'eau.
Cette fiche du site d’Alloprof explique la constante d’acidité :
Cette fiche du site d'Alloprof explique la constante de basicité :
Cette fiche du site d'Alloprof explique la constante d'ionisation de l'eau :
Cette fiche du site d'Alloprof explique la constante du produit de solubilité :
N'hésite pas si tu as d'autres questions!
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Tout d'abord, je te suggère de décrire le mieux possible l'ambiance de la cabane abandonnée. Par exemple, quels bruits peut-on entendre? Quelles sont les odeurs? Est-ce qu'il y a de la lumière à l'intérieur? Etc.
Ensuite, voici quelques idées de questions à te poser :
- Qui a construit la cabane? Est-ce un vieil aventurier, une famille ou quelqu’un qui se cache?
- Que trouve-t-on à l’intérieur?
- Pourquoi est-elle abandonnée?
J'espère que ça te donne un peu d'inspiration!
À bientôt,
Karen
Re: Question
une préposition sert à établir une relation entre deux mots (ex: les amis de Mathilde ---> les amis et mathilde se relient grâce à la préposition "de") tandis qu'une conjonction sert à relier deux phrases (ex: Léo marche. Léo n'aime pas les exercices physiques. on peut le transformer en : Léo marche, mais il n'aime pas les exercices physiques.)
Re: Question
Merci pour ta question!
Pour la première partie de cet exercice, il faut que tu trouves des valeurs de tension nominale de différentes batteries pour ordinateurs et tablette. En général, ces valeurs sont écrites dans une petite police sur le derrière des batteries ou des appareils.
Pour la question 2, essaie de voir si la tension des chargeurs d'autres modèles est la même ou non. Si c'est la même, il devrait être possible de les charger avec le même chargeur.
Pour la question 3, essaie de voir si la tension des chargeurs de différents modèles d'ordinateurs est la même. Si ce n'est pas la même, il est impossible de les charger avec le même chargeur.
Pour la question 4, essaie de penser ce qui se produirait si on survoltait un circuit avec trop de tension, surtout si ce circuit avait plusieurs petites composantes électroniques comme un portable.
Cette fiche du site d'Alloprof explique la mesure de l'intensité du courant :
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour ! Un pourcentage, c'est simplement un fraction qui est sur 100. Par exemple, 25% c'est égal à 25/100, qui est équivalent à 1/4. Je te mets ici un lien vers la fiche en question, en espérant pouvoir t'aider. Bonne chance pour tes examens du ministère !
Re: Question
Salut!
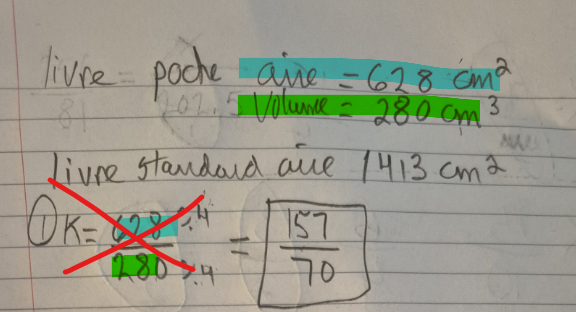
Tu es sur la bonne voie! Cependant, attention, tu ne peux pas calculer le rapport d'une aire sur un volume!
De plus, k est le rapport de similitude pour des mesures de longueur. Tu ne connais ici aucune mesure de longueur. Ce n'est donc pas k qu'il faut commencer par calculer.
Voici ce que tu dois plutôt faire : tu connais l'aire du livre de poche et l'aire du livre standard, tu peux donc commencer par calculer le rapport des aires (k²).
k² = aire du livre de format de poche / aire du livre de format standard
$$k^2 =\frac{ 628}{1413}$$
Maintenant, tu dois ensuite trouver k à partir de k², puis tu pourras trouver k³.
Une fois que tu connais le rapport des volumes k³, tu peux t'en servir pour trouver le volume du livre de format standard :
k³ = volume du livre de format de poche / volume du livre de format standard
k³ = 280 / volume du livre de format standard
Voici une fiche qui pourrait t'être utile : Les rapports de similitude, d'aires et de volumes (k, k², k³) | Secondaire | Alloprof
Je te laisse continuer. J'espère que c'est plus clair pour toi! :)
Re: Question
Bonjour PandaEfficace4839,
Merci beaucoup pour ta question! Les pôles de l’aimant sont ses deux extrémités. L'extrémité qui s’oriente toujours vers le pôle géomagnétique de la Terre est le pôle nord. Son autre extrémité est donc le pôle sud.
Pour ce qui est de ta deuxième question, cela s’explique avec le champ magnétique de ton aimant. En effet, si le même pôle (sud-sud ou nord-nord) essaye de traverser le champ, cela ne fonctionnera pas et il y aura de la répulsion (les deux vont essayer de s’éloigner le plus possible). Toutefois, si les deux pôles opposés se rapprochent, alors il y aura de l’attraction et le deuxième aimant ne sera pas bloqué par le champ magnétique.
Un matériau est magnétique s’il est attiré ou repoussé par un aimant. Cela signifie donc que, dès qu’il y a une réaction entre le matériau et l’aimant, on peut dire que le matériau est magnétique. Cela dépend de la composition du matériau. Par exemple, les matériaux qui sont magnétiques ont souvent du métal à l’intérieur. Puisque le caoutchouc ou le bois ne sont pas composés de métal, ils ne sont donc pas magnétiques.
Les matériaux ferromagnétiques sont des matériaux ou des substances qui sont seulement attirés par l’aimant. Cela signifie donc qu’ils ne peuvent pas être repoussés par l’aimant, comme tu peux le voir dans l’image que tu as mise dans ta question. Ensuite, les ferromagnétiques ne peuvent pas s’attirer entre eux. Comme tu peux le voir dans l’image, si on met plusieurs clous proches les uns des autres, ils ne sont pas attirés. Toutefois, ces matériaux peuvent garder la propriété magnétique pendant un certain temps, comme tu peux l’observer dans l’image où plusieurs clous sont attirés grâce à l’aimant.
Finalement, un champ magnétique est un espace invisible autour de l’aimant dans lesquels il va y avoir des forces magnétiques. Ce sont donc un espace où il va y avoir des forces qui vont permettront d’attirer des objets et d’autres forces qui permettent de les repousser. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Salut!
Pour calculer le pourcentage d’un nombre, tu peux transformer le pourcentage en nombre décimal, puis multiplier ce nombre décimal par le nombre en question.
Par exemple, pour calculer 45% de 200, on multiplie 0,45 par 200 :
$$0,45 \times 200= 90 $$
Une autre façon de faire serait de transformer le pourcentage en une fraction sur 100. On sait que 45% = 45/100. On pose donc l’équation suivante, puisque les fractions doivent être équivalentes :
$$ \frac{45}{100}= \frac{?}{200}$$
Puis, on cherche l’inconnu. On se demande par quoi on peut multiplier 100 pour avoir 200. La réponse est 2. Puisqu’on a multiplié le dénominateur par 2 pour avoir 200, on doit donc multiplier le numérateur par 2 aussi pour obtenir le numérateur de la fraction équivalente sur 200. 45•2=90
$$ \frac{45}{100}= \frac{90}{200}$$
Voici une fiche sur cette notion pour plus d’exemples :
Si tu as d’autres questions, n’hésite pas à nous réécrire! :)
Re: Question
L'aire d'une polygone régulier est
périmètre x apothème /2
donc ici l'aire de la base d'une plateforme est
85.76 x 12.94 /2 = 554.867
et l'on voit d'après le tableau que le coût d'une plateforme est 25 fois l'aire de sa base
donc pour une plateforme orthogonale le coût est
25 x 554.867= 13871.68 $
(curieusement la hauteur des plateformes n'a aucune influence sur le prix)