Best Of

Mise en situation : Le projet de jardin communautaire

L'école secondaire du Quartier Vert lance un projet de jardin communautaire. Les élèves de secondaire 3 sont chargés de planifier l'aménagement de ce jardin. Utilisez vos connaissances en algèbre pour aider à la planification.Partie A : Planification des parcelles (4 points)

1. Le jardin sera divisé en parcelles rectangulaires identiques. Chaque parcelle aura une longueur de (x + 2) mètres et une largeur de (x - 1) mètres.Exprimez le périmètre d'une parcelle en fonction de x. (1 point)
2. Exprimez l'aire d'une parcelle en fonction de x. (1 point)
3. Si le périmètre d'une parcelle est de 18 mètres, trouvez la valeur de x. (2 points)

Partie B : Clôture du jardin (3 points)

1. Le jardin entier, qui est carré, doit être clôturé. Le côté du jardin mesure (2y + 5) mètres.Exprimez la longueur totale de clôture nécessaire en fonction de y. (1 point)
2. Si la longueur totale de clôture disponible est de 100 mètres, trouvez la valeur de y. (2 points)

Partie C : Budget pour les semences (4 points)

• Le budget pour les semences est de 240$. Chaque type de semence a un coût différent :Tomates : 5$ par paquet
• Carottes : 3$ par paquet
• Laitues : 2$ par paquet

1. Si x représente le nombre de paquets de tomates, y le nombre de paquets de carottes, et z le nombre de paquets de laitues :Écrivez une équation qui représente cette situation. (1 point)
2. Si on achète deux fois plus de paquets de carottes que de tomates, et 5 paquets de laitues de plus que de tomates, exprimez y et z en fonction de x. (2 points)
3. Résolvez l'équation pour trouver combien de paquets de chaque type de semence seront achetés. (1 point)

Partie D : Mise en évidence et factorisation (4 points)

1. Pour organiser les outils de jardinage, on construit des étagères. La quantité de bois nécessaire pour différentes parties est exprimée par les expressions suivantes. Factorisez chaque expression :6x + 18 (1 point)
2. 5ab - 15a (1 point)
3. 4x^2 - 12x (1 point)
4. 3xy + 3x - 9y - 9 (1 point)

Voici les réponses:

Partie A:

1. 4x + 2
2. x² + x - 2
3. x = 4

Partie B:

1. 8y + 20
2. y = 10

Partie C:

1. 5x + 3y + 2z = 240
2. y = 2x, z = x + 5
3. 17 paquets de tomates, 34 paquets de carottes, 22 paquets de laitues

Partie D:

1. 6(x + 3)
2. 5a(b - 3)
3. 4x(x - 3)
4. 3(x - 3)(y + 1)

* J'ai demandé a Perplexity de faire la CD1, c'est une intelligence artificielle qui donne des sources fiable. Je te donne ça, si tu veux pas le faire au cas ou se ne serait pas fiable je comprend totalement ta décision, mais si tu veux poser des questions ou bien avoir des exercices supplémentaires je fait juste te le dire que se site existe!

J'espères que ceci t'auras aidée!

Bonjour,

Malheureusement, nous n'avons pas d'exemple de C1, cependant, voici une page où tu peux trouver tous nos exercices :

Pour les C1, je suggère de demander à ton professeur de t'en donner. Si tu as besoin d'aide dans leur résolution, nous sommes là pour toi !

Bonne journée

Salut !

Les triangles sont des polygones composés de trois angles et de trois côtés. On les classes selon certaines propriétés. Voici une fiche qui contient tous les détails dont tu auras de besoin.

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne soirée !

Salut FramboiseAutonome2366 😁

Merci pour ta question!

Pour transformer un nombre fractionnaire en nombre décimal, voici les étapes à suivre.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici un exemple.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Je te laisse la fiche de ces notions ici au besoin pour d'autres exercices.

Écris-nous si tu as d'autres questions. 😊

À bientôt sur la Zone d'entraide! 😎

Salut FramboiseAutonome2366 😁

Merci pour ta question!

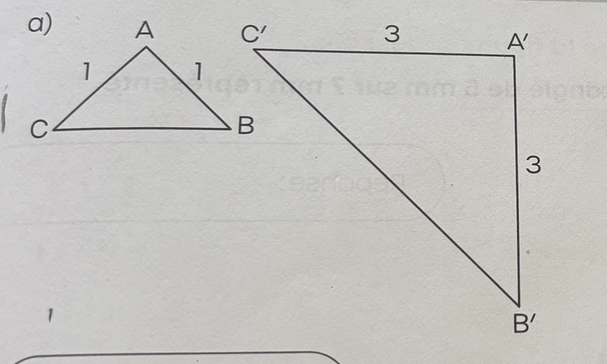
D'abord un côté homologue veut dire qui correspond à.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ici, le côté homologue au côté CB est C'B' (ce sont eux qui se correspondent dans le triangle de gauche et dans le triangle de droite).

Ensuite, pour montrer que les côtés homologues sont proportionnels, ils devront donner le même résultat à chaque division. C'est bon, ça donne bien la même chose.

$$\frac {CA } { C'A' } = \frac {AB } { A'B' } $$

$$\frac {1 } { 3 } = \frac {1 } { 3 } = \frac {1 } {3 }$$

Finalement, il faudra calculer la valeur de CB en chiffre avant de poursuivre et de l'ajouter à notre preuve. Utilise Pythagore!

$$\frac {1 } { 3 } = \frac {1 } { 3} =\frac {CB } {C'B' }= \frac {1 } {3 }$$

Écris-nous si tu as d'autres questions. 😊

À bientôt sur la Zone d'entraide! 😎

Salut CuivreTenace6784 !

Merci d'avoir posé ta question. :)

1) -20 divisé par -2 = 10

Dans ce cas, tu divises -20 en -2 paquets. Bien sûr, si tu veux faire cela dans la réalité, c'est impossible. Par contre, tu dois comprendre ici que le résultat de ta division est simplement le nombre de groupe/paquets dans lequel tu divises ton premier nombre.

Voici un exemple : tu as - 20 bananes, si tu les sépares en -2, tu auras alors 10 paquets (de -2).

2) -7 - 13 = -20

Dans ce cas-ci, il te manque déjà 7, et tu en retires encore 13 (chiffre positif). Combien te reste-t'il ? Il te reste -20.

Voici un exemple : Tu as une carte de crédit qui a 0$ dessus. Cette carte te permet d'emprunter de l'argent, et donc d'aller dans le négatif. Lorsque tu vas au dépanneur, tu achètes un paquet de gomme pour 7$. Tu as donc, -7$ dans ton compte. Le lendemain, tu retournes au magasin acheter un chandail à 13$. Tu fais donc l'opération suivante : -7 - 13 = -20 pour savoir combien tu devras payer à la banque pour rembourser ta carte de crédit.

Voici une fiche qui peut également t'aider à réviser :

J'espère que ces exemples t'aideront à mieux comprendre ! :)

N'hésite pas à repasser si tu as d'autres questions !

À bientôt :)

Salut!

Pour prouver que les côtés homologues sont proportionnels, tu dois poser cette équation :

un côté de la figure image / son côté homologue dans la figure initiale = un autre côté de la figure image / son côté homologue de la figure initiale

Par exemple :

AB / A'B' = AC / A'C'

ou encore :

CB / C'B' = AC / A'C'

En insérant les mesures de ces côtés dans cette égalité, tu peux ensuite vérifier si l'égalité est vraie (si tu as la même chose des deux côtés du =), et si c'est le cas, alors cela signifie qu'il existe un rapport de proportion et donc les figures sont similaires.

J'espère que c'est plus clair pour toi! :)

Salut CitronJaune3021 !

Merci de faire appel à nos services. :)

Le nombre décimal fini est un nombre décimal qui ne continue pas après la virgule.

Par exemple, si j'ai 0,25 qui représente aussi 1/4, le nombre de continue pas à l'infini après la virgule, il se fini à 0,25.

Or, une fraction comme 1/3, représente 0,33... et le nombre 3 (après la virgule) est infini. Il n'est donc pas un nombre décimal fini.

Voici une fiche si tu veux en savoir plus :

N'hésite pas à repasser si tu as d'autres questions. :)

À bientôt ! :)