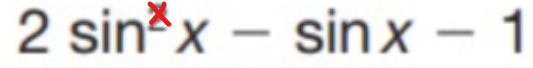Best Of

Bonjour FraiseLibre3245!

Merci de faire appel a la Zone d'entreaide. Je vais te guider pour t'aider a trouver la reponse a ta question.

1. Comprendre la surface d’une pyramide à base rectangulaire

L’aire totale = aire de la base + aire des 4 triangles latéraux.

• Base = longueur × largeur
• Triangles latéraux :
  • Deux triangles sont formés avec la longueur et un apothème (côté long).
  • Deux triangles sont formés avec la largeur et l’autre apothème (côté court).

2. Quel apothème utiliser?

• L’apothème qui est parallèle au côté long sert pour calculer les triangles qui touchent ce côté long.
• L’autre apothème (plus court) sert pour les triangles qui touchent le côté court.

Donc, tu utilises les deux apothèmes, chacun pour son côté correspondant!

3. Formule finale à appliquer (sans résultat)

Aire totale = (aire de la base) + 2 × (aire des triangles longs) + 2 × (aire des triangles courts)

Si tu souhaites obtenir plus d'informations, je t'invite fortement à consulter cette fiche explicative portant sur ce sujet!

L'aire des pyramides | Secondaire | Alloprof

N'hesite pas a revenir nous voir si tu as d'autres questions!

OpalePratique5921

Salut!

Je suis là! :) Je suis super contente que tu aimes mes explications et qu'elles aient pu t'aider, ça me fait très plaisir et c'est justement ça mon but, de t'aider! Cependant, je tiens à te rassurer, mes collègues aussi sont en mesure de t'aider ;) Je ne suis pas sur la Zone tous les jours malheureusement, et nous ne voulons pas que tu restes sans réponse pendant un long délai, ça nuirait à ton apprentissage! :( Donc, ce que je te propose, c'est que tu n'hésites pas à poser tes questions, et si tu n'as pas compris, n'hésite pas à la reposer, et ce, autant de fois qu'il le faut pour que tu comprennes!

De plus, je vois que tu fais beaucoup d'efforts au quotidien, c'est super! Ne dis pas que tu auras une mauvaise note, tu es capable, aie confiance en toi, je suis sûre que tu pourras avoir une excellente note à ton examen cette semaine! 💪

Bon, voyons voir maintenant tes questions de plus près.

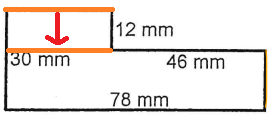
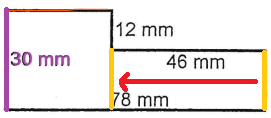
1) Pour mieux comprendre, imaginons qu'on déplace le côté manquant, comme ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La petite droite (en orange) que l'on vient de déplacer est toujours de la même mesure, n'est-ce pas? On l'a simplement fait changer de place.

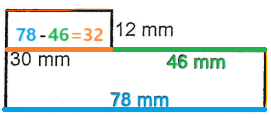
On constate alors visuellement que ce segment orange et le segment vert, ensemble, ils sont égaux au segment bleu :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc, pour trouver la mesure du segment orange, il faudrait soustraire 46 mm de 78 mm :

$$ {\color{Orange} segment~ orange} +  {\color{Green} segment~ vert} =  {\color{Blue} segment ~ bleu} $$

$$ {\color{Orange} segment~ orange} =  {\color{Blue} segment ~ bleu} - {\color{Green} segment~ vert} $$

$$ {\color{Orange} segment~ orange} =  {\color{Blue} 78 ~ mm} - {\color{Green} 46~ mm} = {\color{Orange} 32~ mm} $$

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

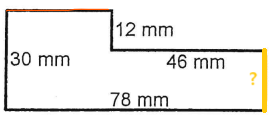
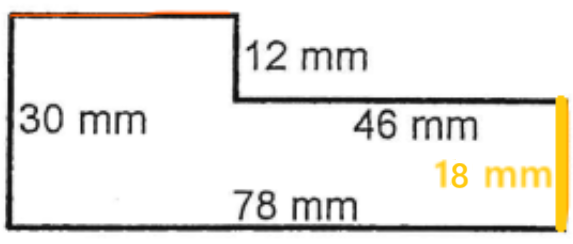
Donc, le segment manquant à l'horizontale est de 32 mm :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Il est important que tu comprennes que tu ne dois pas soustraire une mesure qui est à l'horizontale d'une mesure qui est à la verticale (ou l'inverse) ! Tu avais dit : "est-ce que je devrais faire 78mm - 30mm?". Non, tu ne peux pas faire cela! Le 30 cm est une mesure verticale (l), et le 78 mm est une mesure horizontale (-), les soustraire ne nous donnerait aucune information!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

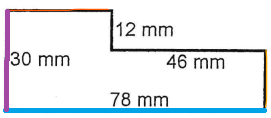
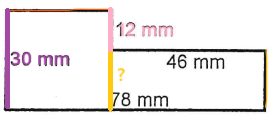
Donc, je te conseille d'essayer de visualiser le déplacement d'une ligne dans ta tête. Faisons la même chose pour trouver l'autre mesure manquante, soit celle-ci, en jaune :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On va la déplacer comme ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On peut alors voir que notre segment jaune de mesure inconnu et notre segment rose de 12 mm sont de la même mesure que le segment mauve de 30 mm si on les combine ensemble!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc, pour trouver la mesure du segment jaune, il faut faire ce calcul :

$${\color{Purple} 30~mm}-{\color{Pink} 12~mm}={\color{Orange} 18~mm}$$

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

En résumé, assure-toi de soustraire des mesures qui sont dans la même orientation (vertical et vertical, ou horizontal et horizontal). Tu peux aussi visualiser le déplacement d'une droite pour qu'elle soit alignée avec une autre comme on l'a fait.

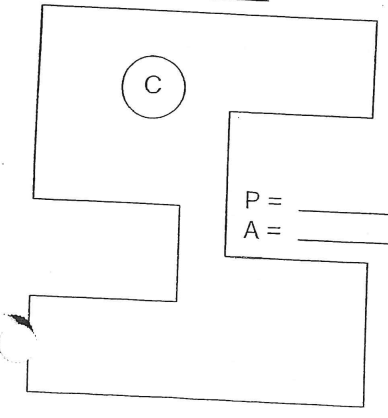
2) La formule d'aire L × l permet de trouver l'aire d'un rectangle ou d'un carré. Si tu as une figure qui n'est pas une forme usuelle (comme un rectangle, un carré, un triangle, etc.), comme ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

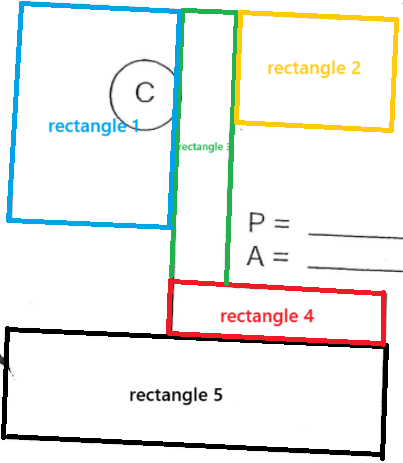
dans ce cas, tu dois décomposer cette figure en des petits rectangles ou des petits carrés! Voici un exemple :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On a décomposé notre grande figure initiale en 5 rectangles de différente taille!

Pour trouver l'aire totale de la figure initiale, il faut donc additionner l'aire de chacun de ces rectangles :

Aire totale = Aire rectangle 1 bleu + aire rectangle 2 jaune + aire rectangle 3 vert + aire rectangle 4 rouge + aire rectangle 5 noir

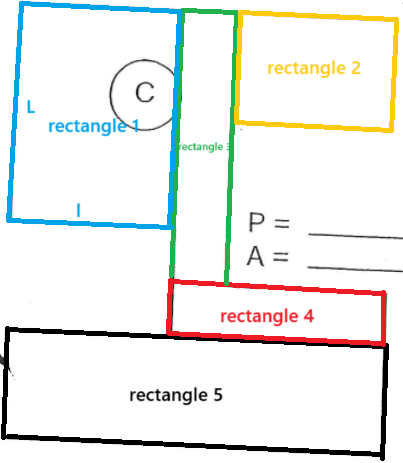
Pour trouver l'aire de chacun de ces rectangles, tu peux utiliser la formule L × l. Attention, assure-toi de prendre la longueur et la largeur du rectangle dont tu calcules l'aire! Par exemple, si je calcule l'aire du rectangle 1 bleu, je vais prendre cette largeur et cette longueur :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

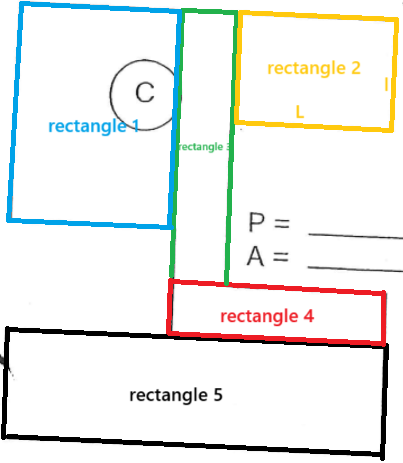
Mais si je suis rendu à calculer l'aire du rectangle 2 jaune, c'est cette longueur et cette largeur qu'il faut utiliser :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, il est super important que tu trouves d'abord toutes les mesures que tu as besoin. Pour cela, il se peut que tu aies à trouver des mesures manquantes, comme on a expliqué précédemment à ta question 1).

3) Au primaire, tu vas calculer le volume des prismes à base rectangulaire seulement (au secondaire, tu étudieras les pyramides, les cylindres, les cônes, les sphères, etc.).

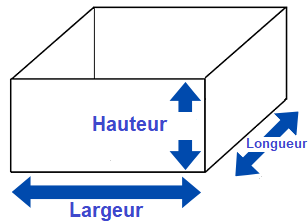
Donc, tu dois utiliser la formule suivante pour calculer le volume :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

En d'autres mots, tu dois simplement multiplier les trois mesures de ton solide!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

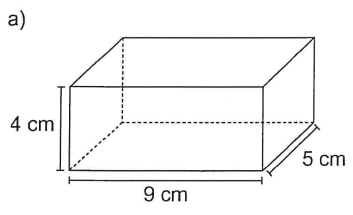
Ainsi, dans ton exercice :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu dois multiplier les trois mesures pour trouver le volume de ce solide :

$$V=4 \times 9 \times 5 = 180$$

Le volume est donc de 180 cm³ :)

Voilà, je crois que l'on a fait le tour de tes questions. J'espère que cela t'aidera à mieux comprendre la matière! Je quitte pour aujourd'hui, mais, ne t'inquiète pas, je te laisse entre de bonnes mains! Donc, comme je te l'ai expliqué, si tu n'as pas compris quelque chose dans mon explication ou si tu as d'autres questions ce soir, n'hésite surtout pas! Mes collègues sont tous super doués et seront en mesure de t'aider! :) À la prochaine! 😁

Salut!

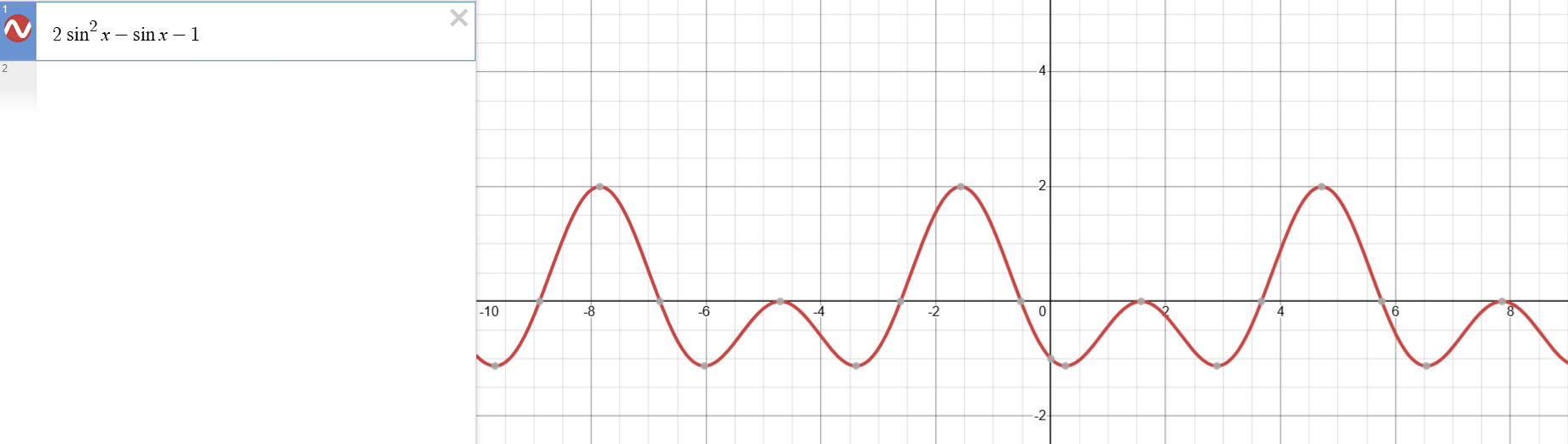
Il ne s'agit pas d'une fonction sinus normale!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Cette fonction est une expression trigonométrique de second degré. Donc, puisque nous n'avons pas la forme d'une fonction sinus pure (\(f(x)=asin(b(x-h))+k\)), on ne va pas chercher les paramètres a, b, h et k comme on a l'habitude de faire ;)

Ce genre de fonction n'est pas du tout au programme du secondaire (ni même du collégial je crois), donc ne t'inquiète pas, on ne te demandera jamais de travailler avec des fonctions ayant plusieurs sinus de différent degré.

Or, si nous n'avions pas eu ce petit exposant 2 :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Alors la fonction sinus pourrait se simplifier comme ceci :

$$f(x)=2sinx-sinx-1$$

$$f(x)=2sinx-1sinx-1$$

$$f(x)=(2-1)sinx-1$$

$$f(x)=1sinx-1$$

$$f(x)=sinx-1$$

Sous forme canonique, on peut écrire :

$$f(x)=1sin(1(x-0))-1$$

En d'autres mots, nos paramètres sont :

• a = 1
• b =1
• h = 0
• k = -1

J'espère que cela t'aide! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Salut!

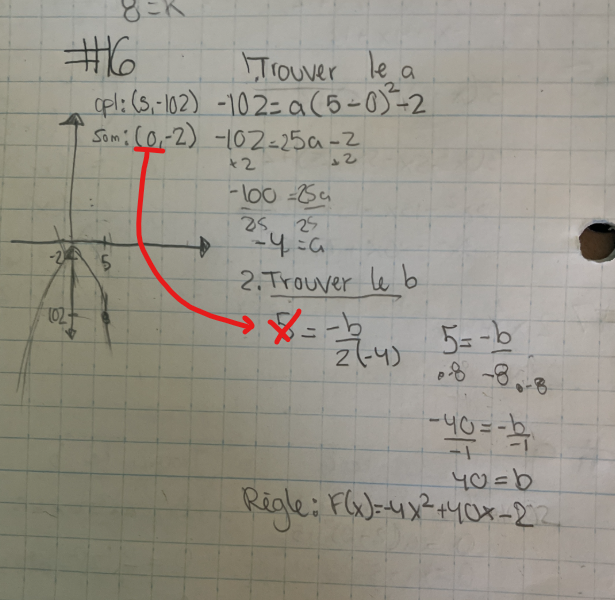
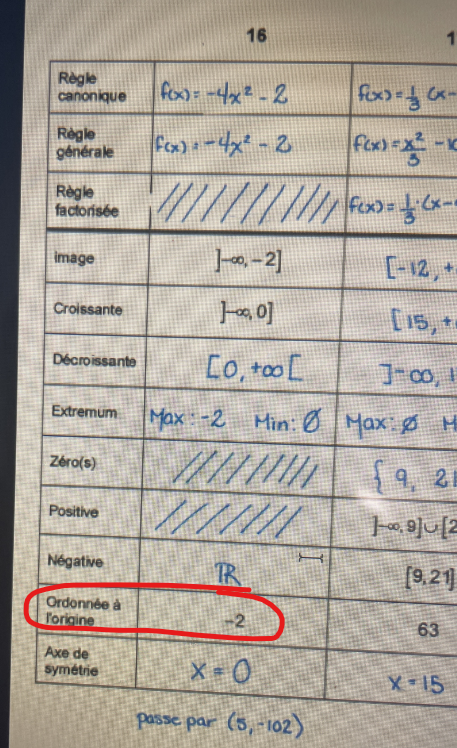
Ta démarche est bonne, tu as simplement fait une petite erreur d'inattention! ;) Au lieu de prendre h=0, tu as pris h=5 dans ce calcul :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu as probablement pris par accident la coordonnée en x du point donné (5, -102) parce que tu l'as inscrit juste en haut des coordonnées du sommet. En prenant la bonne valeur de h, tu obtiendras b=0 :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$h=\frac{-b}{2a}$$

$$0=\frac{-b}{2(-4)}$$

$$0=\frac{-b}{-8}$$

$$0=\frac{b}{8}$$

$$0 \times 8=\frac{b}{8} \times 8$$

$$b=0$$

Puisque b=0, alors on a l'équation :

$$f(x)=-4x^2+0x-2$$

$$f(x)=-4x^2-2$$

De plus, il y a bien une ordonnée à l'origine, on te la donne justement :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

En plus, le paramètre c de la forme général correspond justement à l'ordonnée à l'origine de la fonction! ;)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La fiche suivante présente une démarche alternative pour passer de la forme canonique à la forme générale : Les formes d'écriture de la fonction polynomiale de degré 2 | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Bonjour,

Oui, un triangle isocèle est nécessairement isoangle.

De plus, un triangle isocèle peut aussi être rectangle. Pour cela, il doit posséder un angle droit et deux angles égaux de 45°.

Bonne journée :)

Si tu as d'autres questions, n'hésite pas !