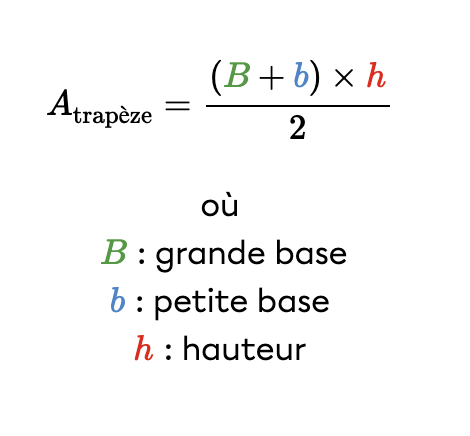Best Of
Re: Question
Salut, FramboiseRouge3406!
Merci pour ton commentaire, nous sommes ravis que tu aies eu une bonne expérience! Je vais passer le mot à Océane que tu étais satisfait(e) de ses explications. 😇
N'hésite pas à nous réécrire! À bientôt! :)
Iris
Re: Question
salut moi mon prof de science dit on doit toujours garder au moins 2 chiffres apres la virgule et on doit arrondir lorsqu'on a plus de 3 comme par exemple avec pi qui est 3.1415.... on fait gnr 3.14
Re: Question
Bonjour FraiseTurquoise2087 !
Merci d'utiliser la zone d'entraide. :)
Ton travail semble bien complété. Fait attention aux symbols de négation. Si l'écart entre les températures baisse, tu dois mettre le « - » avant le chiffre.
Voici une fiche sur les nombres négatifs et positifs si tu as besoin :
N'hésite pas à repasser nous voir si tu as d'autres questions! :)
Angélique
Re: Question
Salut PandaSolidaire1774 !
Merci d'utiliser la zone d'entraide. :)
Tout d'abord, voici notre fiche sur comment bien bâtir sa feuille de note :
Ensuite, nous avons un répertoire de révision pour t'aider à cibler la matière à mettre sur ta feuille de note.
Le voici :
Tu peux aussi :
- Séparer ta feuille par section ou par chapitre ;
- Écrire chacune des formules ;
- Bien t'exercer et étudier ;
- Inscrire des exemples sur ta feuille de note.
En mathématique l'important c'est de savoir comment utiliser les formules. :)
J'espère que cela répond à ta question. Je te souhaite une bonne étude et un bon succès à ton examen !
N'hésite pas à repasser si tu as d'autres questions. :)
Angélique
Re: Question
Salut PandaSolidaire1774 !
Merci d'utiliser la zone d'entraide. :)
Nous avons justement une fiche d'alloprof sur comment se préparer à l'écriture d'un texte argumentatif :
Voici une fiche sur la structure :
Ainsi que la structure :
Voici aussi une fiche sur comment bien faire ta feuille de note :
N'hésite pas à repasser si tu as d'autres questions ! :)
Bonne rédaction !
Angélique
Re: Question
Coucou FraiseComique6111 !
Merci d'utiliser la zone d'entraide. :)
Il existe plusieurs façons de trouver une mesure manquante dans une figure plane.
Voici une fiche qui te donne plusieurs exemples :
Ci-dessus tu trouveras la formule de l'aire du trapèze. Il est possible de trouver une mesure manquante à partir de la formule en faisant de l'algèbre (en isolant le terme manquant).
Par exemple, si tu as l'aire totale mais qu'il te manque la hauteur, tu peux isoler h pour trouver ta hauteur.
De plus, il se peut que tu retrouve un rectangle bien défini au milieu de ton trapèze, ce qui t'aiderait à trouver sa hauteur car sa formule de l'aire est Longueur x largeur. Encore une fois tu devras utiliser l'algèbre pour isoler la L pour trouver la hauteur du trapèze.
Enfin, si tu as toujours besoin d'aide tu peux nous envoyer une photo de ton exercice afin que l'on puisse mieux t'aider.
N'hésite pas à repasser si tu as d'autres questions ! :)
Angélique
Re: Question
Bonjour FraiseComique6111 !
Merci d'avoir posé ta question. C'est une question qui correspond bien au thème de la journée ! 🐣🐰
Il est vrai de dire que lorsqu'on prononce oeuf (au singulier), on prononce le son [f] à la fin, alors que quand oeufs est au pluriel, on ne prononce plus le [f] à la fin.
Dans la phrase : « J'ai neuf oeufs. », on respecterait la règle. Le chiffre neuf se prononce avec le [f] à la fin, mais pas oeufs.
Cela ferait une phrase qui sonne ainsi : « J'ai neuf oeu. »
N'hésite pas à repasser si tu as d'autres questions. :)
Angélique
Re: Question
Salut TortueTenace6185 !
Merci d'utiliser la zone d'entraide. :)
Tu as envoyé deux fois la même image, je vais donc t'aider avec ce premier numéro, mais n'hésite pas à nous envoyer ta 2e image si tu veux de l'aide.
Alors, voici ce que tu sais :
- L'eau doit être au 7/8 de la hauteur de l'aquarium.
- L'aire latérale de l'aquarium est de 3070,8 cm2.
- Ton cylindre à une circonférence de 20 cm.
- La droite de ton prisme à base rectangulaire mesure 30 cm.
Voici ce que tu cherches :
- Le 7/8 de la hauteur de l'aquarium.
Pour trouver ta réponse, tu dois d'abord faire plusieurs étapes.
Comme tu connais l'aire latérale et quelques mesures, as-tu une façon de trouver les mesures manquantes de ton aquarium ? (En travaillant avec les formules, par exemple!)
Ensuite tu devras trouver l'équivalence du 7/8 de la hauteur du cylindre.
Voici une fiche sur l'aire des cylindres :
Base de la face latérale =
Circonférence du cercle
Hauteur de la face latérale = Hauteur du cylindre
⇒ Aire de la face latérale = Circonférence × Hauteur
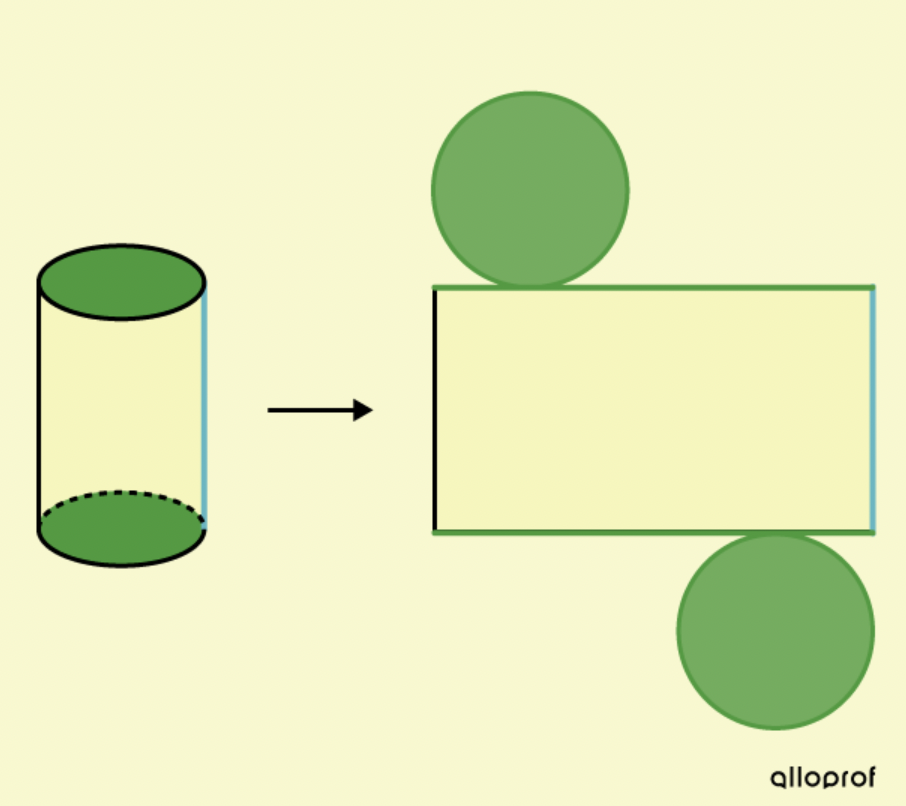
Voici un petit rappel de la construction du cylindre (deux cercles et un rectangle!) :
Je te laisse essayer de débuter cette situation-problème seul.e, mais n'hésite pas à repasser si tu as d'autres questions.
Angélique
Question
Bonjour mon prof m’a pas mis le corrigé de cet exercice et j’ai un examen mardi.
Re: Question
Bonjour ElfeHumble179 !
Merci d'avoir posé ta question.
Malheureusement, nos services sont seulement en français et en anglais pour l'instant.
N'hésite pas à utiliser des outils de traductions pour communiquer avec nous.
N'hésite pas si tu as d'autres questions ! :)
Traduction en espagnol par google traduction :
¡Hola ElfeHumble179!
Gracias por hacer tu pregunta.
Por el momento nuestros servicios sólo están disponibles en francés e inglés.
No dude en utilizar herramientas de traducción para comunicarse con nosotros.
¡Si tienes alguna otra pregunta no dudes en preguntar! :)
Angélique