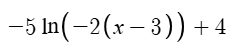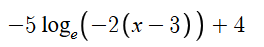Best Of
Re: Question
Bonjour JujubeSuperbe6597 !
Dans mon ordinateur et dans mon téléphone j'ai un problème qui est semblable au tien. Mon problème est que quand j'entre directement sur Alloprof, il me disent: Tous les résultats (0). Même lorsque je tape une matière ou un sujet d'une matière, ça me met: Tous les résultats (0).J'ai essayer tout les moyens que j'ai pu mais, je n'arrive pas à le faire marcher <<correctement>>. Aussi, il n'y a aucun filtre.
Peut-être que tu peux essayer de complètement fermer Alloprof et le rouvrir par la suite ? Sinon ferme ton ordi au complet et essaye à nouveau !
En souhaitant que tu réussisses à faire marcher Alloprof,
SoleilInoubliable8340
Re: Question
Salut!
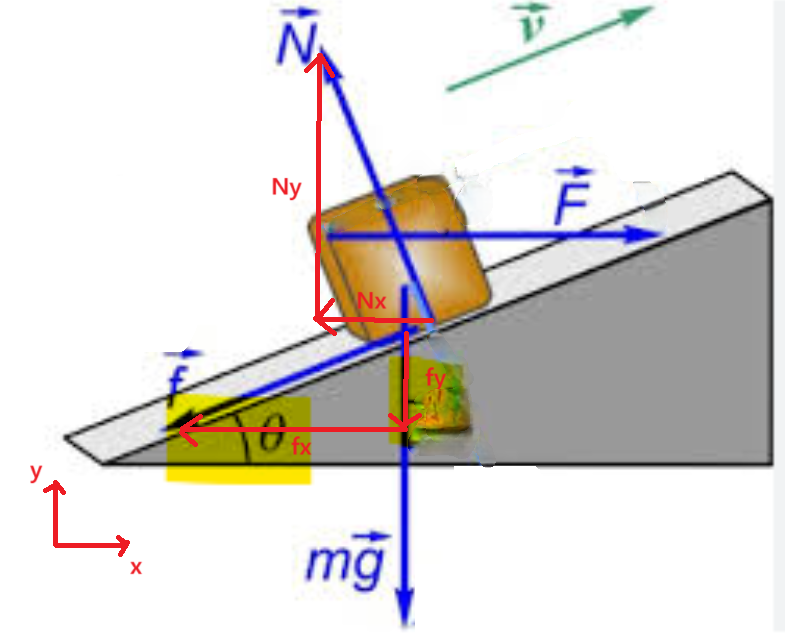
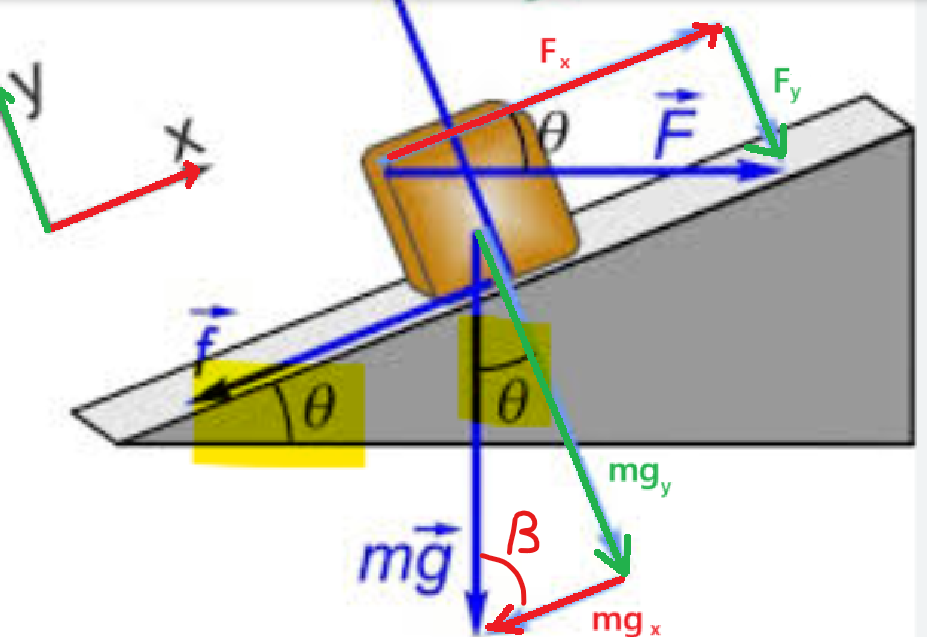
Tout d'abord, pour mieux comprendre, imaginons que nous avons le référentiel usuel, avec l'axe des \(x\) à l'horizontale et l'axe des \(y\) à la verticale :
Dans ce cas-là, notre poids \(m\overrightarrow{g}\) serait orienté vers l'axe négatif des y, donc elle n'aurait pas de composante en x, n'est-ce pas? Même chose pour la force de poussée \(\overrightarrow{F}\), elle serait orientée vers l'axe des \(x\), donc nous n'avons pas besoin de la décomposer, puisqu'elle n'a pas de composante en \(y\).
Cependant, il faudrait décomposer la force de frottement et la forme normale. Donc, on doit toujours décomposer une force selon les axes \(x\) et \(y\) de notre référentiel si elle n'est pas déjà parallèle à l'un des axes. Ainsi, c'est les composantes de ces forces qui seront parallèles aux axes. Par exemple, on voit dans le dessin ci-dessus que la composante en \(x\) de la force de frottement, soit \(f_{x}\), est parallèle à l'axe des \(x\), et la composante en \(y\), soit \(f_{y}\), est parallèle à l'axe des \(y\). Même chose pour la force normale, ses composantes \(N_{x}\) et \(N_{y}\) sont parallèles aux axes de notre référentiel.
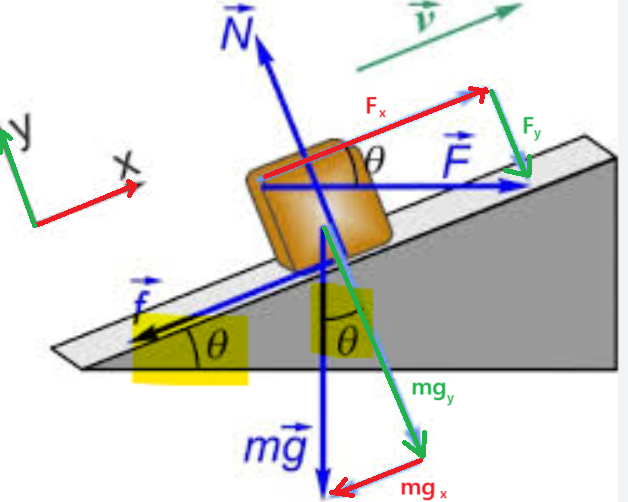
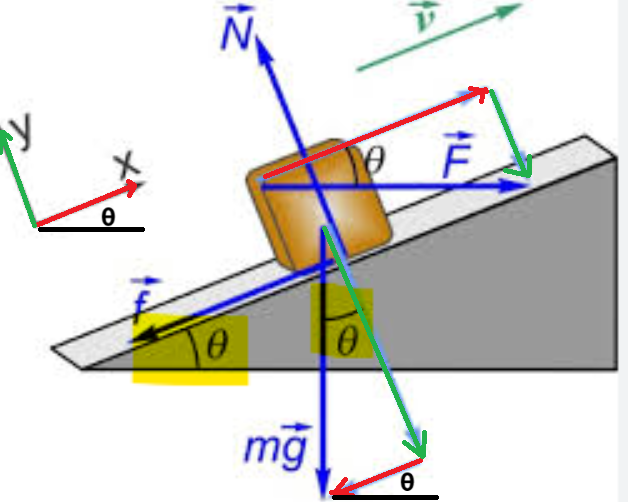
Si on modifie notre référentiel en lui donnant une inclinaison par rapport à l'horizontale, le principe reste le même.
Les forces qui sont déjà parallèles à l'un des axes, donc ici \(\overrightarrow{g}\) (qui est parallèle à l'axe des x) et \(\overrightarrow{N}\) (qui est parallèle à l'axe des y) n'ont pas besoin d'être décomposée, puisqu'elles ont une seule composante qui équivaut à la norme du vecteur et une autre composante nulle (\(N_{x}=||\overrightarrow{N}||\) et \(N_{y}\)=0, et \(f_{x}=||\overrightarrow{f}||\) et \(f_{y}\)=0).
Pour les autres forces qui ne sont pas déjà parallèles à l'un des axes du référentiel que l'on a, donc ici \(\overrightarrow{F}\) et \(m\overrightarrow{g}\), il faut les décomposer de façon à former un triangle rectangle dont les cathètes (les composantes) sont parallèles aux axes de notre référentiel! C'est pourquoi la force \(m\overrightarrow{g}\) est décomposé en \(mg_{x}\) (qui est parallèle à l'axe des x) et \(mg_{y}\) (qui est parallèle à l'axe des y)! Même chose pour \(\overrightarrow{F}\) , que l'on décompose en \(F_{x}\) et \(F_{y}\).
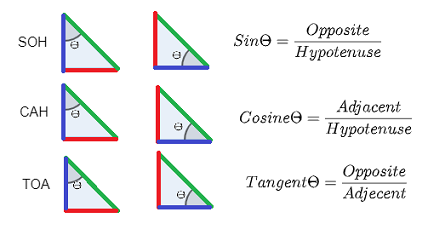
Maintenant, pourquoi sinus pour x, pourquoi cosinus pour y? C'est une question de trigonométrie dans le triangle rectangle! Ce n'est pas toujours sinus pour x et cosinus pour y, ça dépend de l'angle que l'on utilise! Il faut se rappeler notre truc : SohCahToa!
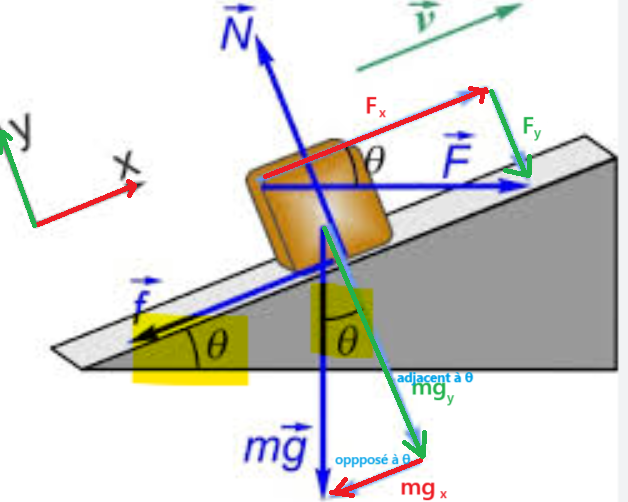
Ainsi, le côté opposé à l'angle θ est \(mg_{x}\). Donc, il faut utiliser le rapport sin (SohCahToa) pour trouver la composante en x du poids. De la même façon, le côté adjacent à l'angle θ est \(mg_{y}\). Donc, il faut utiliser le rapport cos (SohCahToa) pour trouver la composante en y du poids.
Si on voulait plutôt utiliser l'angle β suivant (qui équivaut à 180-90-θ) :
Alors, le côté opposé à l'angle β serait \(mg_{y}\), donc il faudrait utiliser sin (SohCahToa) pour trouver la composante en y de la force. Le côté adjacent à l'angle β serait \(mg_{x}\), donc il faudrait utiliser cos (SohCahToa) pour trouver la composante en x de la force.
On voit donc qu'on doit trouver le rapport trigonométrique à utiliser selon l'angle que l'on utilise! :)
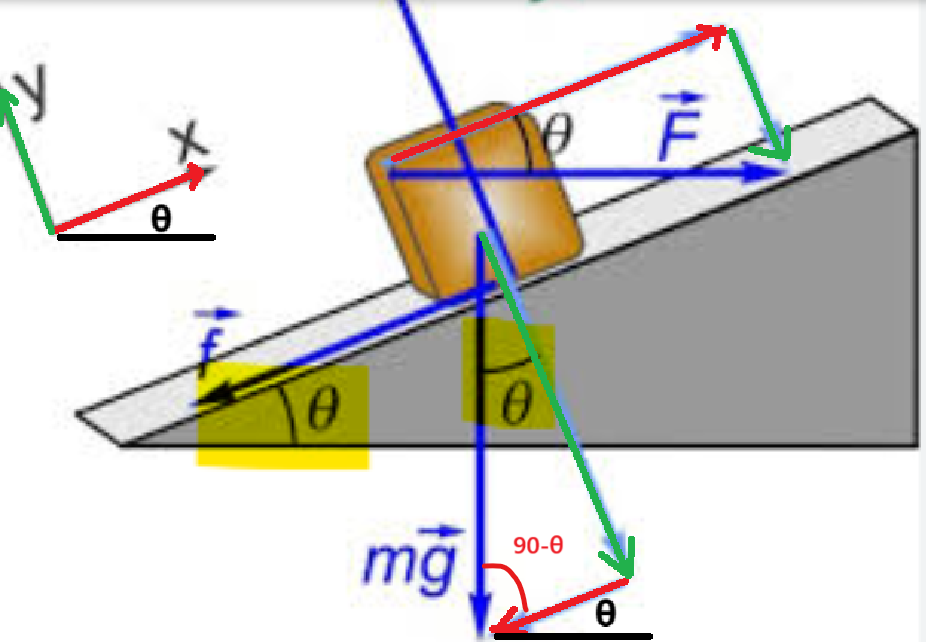
Ensuite, concernant ta seconde question, il faut utiliser nos différentes relations entre les angles pour arriver à cette conclusion. On se rappelle que notre référentiel est parallèle au plan incliné, donc son axe des x a un angle de θ par rapport à l'horizontale. Puisque la composante en x du poids est parallèle à l'axe des x, alors elle aussi possède un angle de θ par rapport à l'horizontale :
Donc, l'angle suivant est de 90-θ:
Donc, l'angle que tu as souligné en jaune est de 180 - 90 - (90-θ), ce qui équivaut à θ ! :
$$180 - 90 - (90-θ)$$
$$=90-(90-θ)$$
$$=90-90+θ$$
$$=θ$$
Voilà! J'espère que c'est plus clair pour toi! :)
Re: Question
Salut!
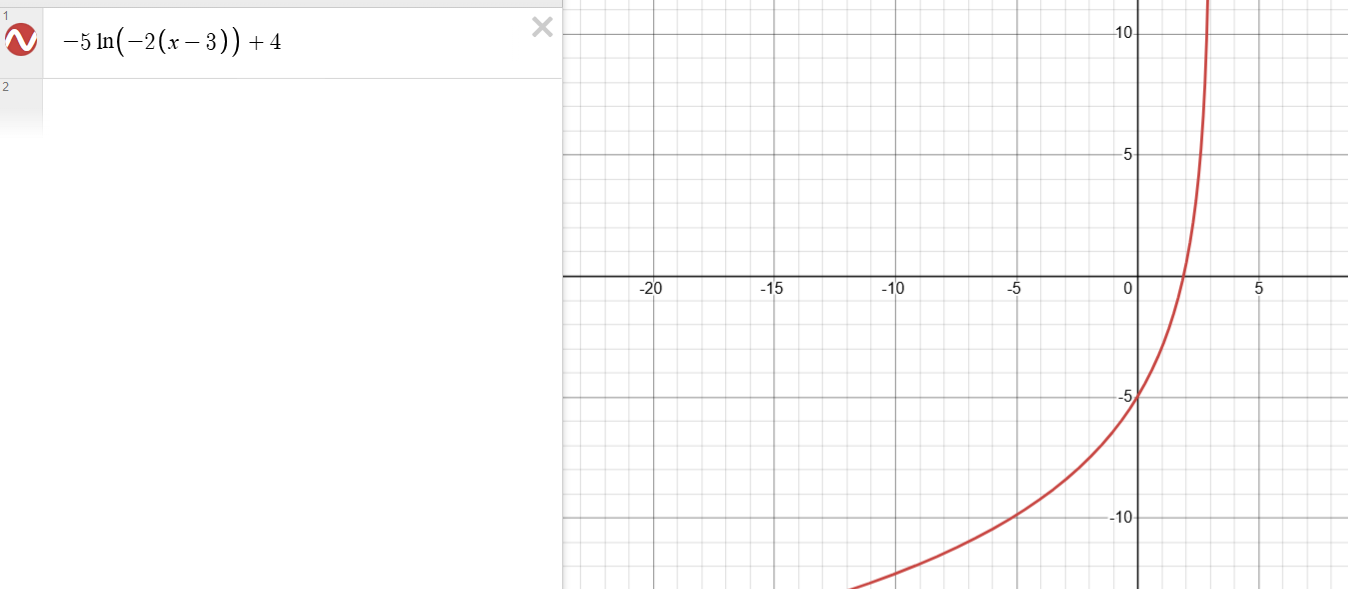
En effet, la fonction est croissante :D
Sans graphique, pour une fonction logarithme sous forme canonique, on peut analyser les paramètres a, b et c pour déterminer la croissance ou la décroissance.-2.La fonction est croissante si :
La fonction est décroissante si :
On a l'équation :
qui équivaut à :
Donc, les paramètres sont : c=e≈2.71828, a=-5 et b=-2. Puisque c est supérieur à 1 et que a et b sont de même signe, alors la fonction est croissante.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
Un effectif est le nombre de fois qu’une donnée est présente dans une distribution. Par exemple, dans ton exercice, le nombre 42 n'est présent qu'une seule fois, donc son effectif est de 1. Le nombre 62 est présent trois fois, donc son effectif est de 3.
Un tableau d'effectifs est donc un tableau où l'on donne l'effectif de chaque donnée de la distribution!
Voici un exemple :
Je te laisse essayer avec ces indices. Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Question
Bonsoir ! Merci beaucoup pour vos beaux compliments ! Cela m'a vraiment touchée !
Bref, j'ai une question ! Pouvez-vous me dire des choses sur le sujets, les aspect et les sous-aspects. Je comprend bien la matière mais je dois faire un projet d'écriture (qui est pour demain) et il y a une question qui est à propos de cela. Veuillez me répondre avant demain S.V.P.
Bonne soirée
SoleilInoubliable8340
Re: Question
Salut!
Tu as bien raison! SoleilInoubliable8340 prend souvent le temps d’aider les autres avec respect et bienveillance. Un énorme merci à cet(te) élève pour son implication sur la Zone d’entraide! 😁
Merci également à toi, PapillonRose9836, pour ton message positif! Ça fait toujours super plaisir de voir de la reconnaissance entre les élèves! :)
Si tu as d'autres questions, n'hésite pas à nous réécrire! À la prochaine! :)
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Tu devrais normalement avoir reçu un lien dans le courriel qui te permet de participer.
Si tu ne le trouves pas ou que tu as des questions, n'hésite pas à écrire à notre équipe de soutien en cliquant sur le lien suivant:
Bonne chance pour le concours!
Karen
Re: Question
Salut! Voici des étapes pour t'éclairer : On sait que le résultat final est 30 après plusieurs opérations. On va refaire les étapes en remontant à l'envers pour trouver le nombre de départ.
- Le dernier calcul était une division par 4 → Pour revenir en arrière, on fait l'opération inverse : multiplier par 4 30×4=120
- Avant, on avait ajouté 24 → Pour revenir en arrière, on fait l'opération inverse : soustraire 24 120−24=96
- Avant, on avait multiplié par 3 → Pour revenir en arrière, on fait l'opération inverse : diviser par 3 96÷3=32
- Avant, on avait ajouté 5
- → Pour revenir en arrière, on fait l'opération inverse : soustraire 5 32−5=27
Réponse : Kallysha pensait au nombre 27. ✅
Reviens-nous si tu as encore besoin d'aide! :)
Andréanne pour AlloProf!
Re: Question
Bonsoir! :)
Nous pouvons certainement t'aider! :)
Quelle est ta question?
À tout de suite!
Sarah G