Best Of
Re: Question
Bonjour Béatrice,
Nous sommes tellement réjouis d'entendre cela :D On te remercie d'utiliser les services Alloprof et nous t'encourageons à continuer ;)
En théorie, un nombre carré est un nombre que l’on peut représenter par un carré ou une suite de carrés imbriqués.
Il peut être tôt de savoir cela, mais puisque tu as demandé de savoir plus, la suite des nombres carrés est : 1, 4, 9, 16, … n² où n représente à la fois le rang du terme dans la suite et le nombre de points sur le plus grand carré de la figure.
En gros, un nombre carré est formé par un nombre que l'on multiplie par lui-même.
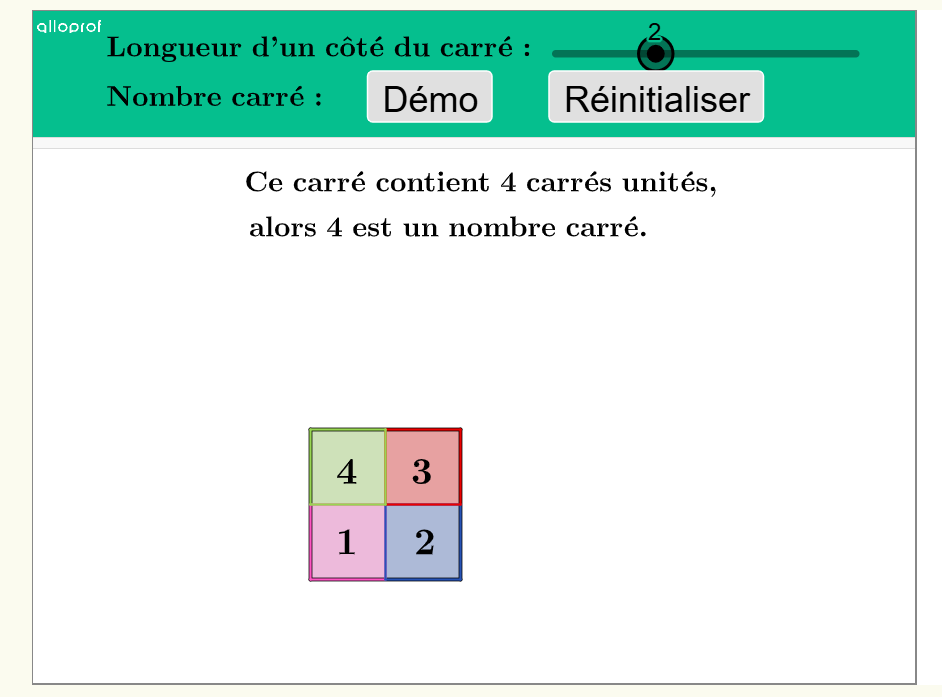
Par exemple, 4 est un nombre carré, car c'est 2 x 2.
D'autres exemples sont 25, car 5x5=25, 64, car 8x8=64, etc.
Puisqu'il s'agit d'un nombre multiplié par lui même, un nombre carré s'exprime en notation exponentielle, donc le nombre élevé au carré (d'où vient le nom).
Petite note didactique: Le nombre 0, qui est le carré du nombre naturel 0, n’est pas un nombre carré.
Pour plus de détails, consulte la fiche Les nombres carrés et cubiques | Secondaire | Alloprof .
J'espère que ça va t'aider à mieux comprendre tes exercices ;)
Re: Question
Bonjour, ChevalierAlpha6568!
Merci d'utiliser la Zone d'entraide!
Un ion polyatomique est un ion formé d’un groupe d’atomes liés entre eux, formant une entité stable avec une charge électrique globale, positive ou négative.
En voici quelques exemples:
Voici la fiche dans laquelle tu retrouveras ces informations:
Si tu as d'autres questions, n'hésite pas à nous réécrire!
Iris
Re: Question
Bonsoir, CigogneFantastique9219!
Selon la formule précédente, tu peux déduire que la deuxième doit prendre en considération la circonférence des bases également, puis la hauteur inclinée.
Ainsi, l'aire latérale d'un tronc de cône est
$$ A_L=\frac{(C_{GB}+C_{PB} ) \cdot a}{2} $$
où
$$ C_{GB}:\text{Circonférence de la grande base} $$
$$ C_{PB}:\text{Circonférence de la petite base} $$
N'hésite pas à poser d'autres questions!
Re: Question
L'agriculture extensive se pratique sur des grandes surfaces de terre et exige moins de travail. Les rendements sont faibles. La définition est dans cette page d'Alloprof
Re: Question
Salut!
Tu peux utiliser notre répertoire de révision :D Tu y trouveras toutes les notions étudiées en histoire de secondaire 4 😋 Voici le lien : Répertoire de révision – Histoire du Québec et du Canada – Secondaire 4 | Secondaire | Alloprof
Bonne étude! :)
Re: Question
Salut!
Pour apprendre tes tables de multiplication, il n'y a vraiment qu'un seul moyen, la PRATIQUE! ;) Le secret est de se pratiquer le plus possible, et tu verras que bientôt, tu les réciteras comme sur le bout de tes doigts!
Voici des jeux qui te permettront de pratiquer tes tables tout en t'amusant : Météormath et Fin Lapin.
Je te conseille aussi d'aller jeter un coup d'œil à la fiche suivante, tu y trouveras diverses astuces pour t'aider à apprendre tes tables par cœur : Trucs pour apprendre les tables par coeur | Alloprof
De plus, sur ce site, tu trouveras des astuces pour chacune des tables de multiplication, tu n'as qu'à cliquer sur la table souhaitée : https://universites-numeriques.fr/table-de-multiplication/
En les révisant régulièrement, je suis sûre que tu deviendras un pro très rapidement! À toi de jouer maintenant! :D
Re: Question
Salut GrenatSage8065 !
Merci d'utiliser la zone d'entraide. :))
Le foyer récepteur, dans le contexte du tourisme, est la partie du monde qui accueille des touristes.
Par exemple, on peut dire que la France est un foyer récepteur, car elle accueille plusieurs touristes chaque an.
Bonnes études!
BismuthSarcelle3150
Re: Question
Salut Melisa,
Merci pour ta question!😊
Pour trouver la hauteur de ton triangle, tu dois regarder les quadrillés de ton dessin. Tu sais que 2 carrées correspondent à (3a^2-8a) et si tu regardes ton triangle, la hauteur correspond à deux carrées. Ainsi, la hauteur de ton triangle est de (3a^2-8a).
Pour ce qui est de l'aire, si tu regardes le diamètre de demi-cercle, tu peux qu'il correspond à la base du triangle. Il ne te reste plus qu'à utiliser la formule de l'aire et tu as ton expression algébrique.
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!😉
Anthony B.
Re: Question
Bonjour DiamantLogique8620,
Merci pour ta question :)
Le dx dans une intégrale indique l’élément infinitésimal de la variable d’intégration. En d’autres termes, il précise par rapport à quelle variable on intègre. Si tu as par exemple l'intégrale de f(x)dx, tu dois calculer la somme de la fonction f(x) sur des intervalles de largeur infinitésimales dx. C'est donc important de comprendre que dx n'est pas une variable.
Lorsqu’on intègre une fonction, on trouve la fonction primitive. Le dx n’a plus besoin d’être écrit car il a joué son rôle : spécifier la variable et guider l’intégration.
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Bonjour Loupmauve,
- Égalité : Une égalité est une relation mathématiquesvérifiable où les deux côtés de l'équation sont équivalents. Exemple : 2 + 2 = 4
- Équation : Une équation ressemble à un problème à résoudre. C'est une égalité mathématique impliquant une ou plusieurs variables pour lesquelles on cherche la ou les valeurs la rendant vraie. Exemple : 10 = 2x + 2
Une expression n'a pas d'égalité; c'est une phrase mathématique.
- Expression algébrique : Une expression algébrique est une phrase mathématique avec des variables, mais sans égalité. Par exemple, j'ai 4 ans de plus la moitié de l'âge de ma mère. Si on dit que l'âge de ma mère est X, alors, j'ai X/2 + 4.
- Expression numérique : Une expression numérique est une phrase mathématique sans variable. Les additions, soustractions, multiplications, divisions sont des expressions numériques.
N'hésite pas à nous réécrire si tu as d'autres questions ! :)
- Noémie