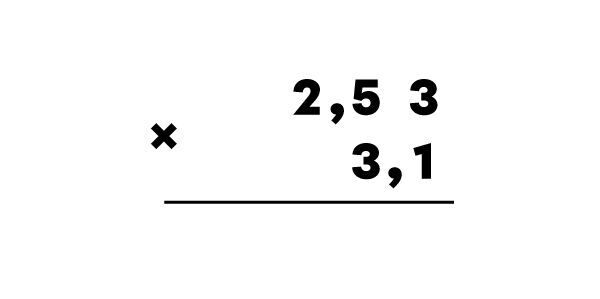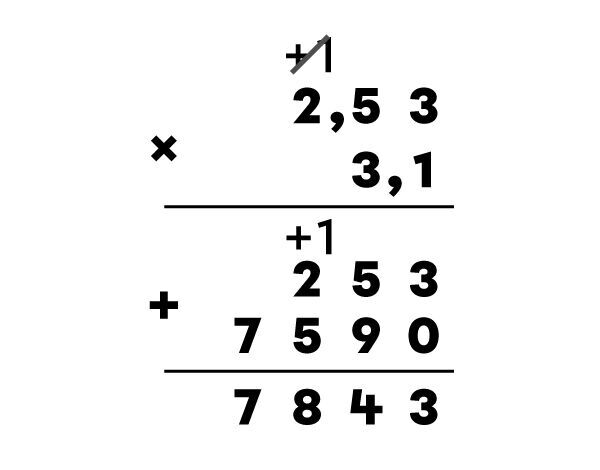Best Of
Re: Question
Salut !
Pour chacune des sous-questions, il te faudra utiliser des équations MRUA.
Pour te simplifier la tâche, tu énumères les données connues et celles que tu veux calculer. Dans le a), grâce au graphique, tu connais les vitesses initiales et finales ainsi que le temps. Tu peux ainsi calculer le déplacement à l'aide de la formule suivante.
$$ \triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2} $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Tu as deux aspect à analyser. Le premier est de connaître le sens de la vitesse par rapport au référentiel \(x\).
Et le deuxième est de déterminer si la vitesse varie ou non (avec ou sans accélération). Prenons l'exemple du a). La vitesse est de la direction inverse de \(x\), elle donc négative. De plus, elle varie en fonction du mouvement/temps en étant de plus en plus négative. Ce mouvement est donc lié au a).
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Bonjour!
Nous n'avons pas de document qui explique spécifiquement des stratégies qui permettent de favoriser un dialogue constructif. Cependant, à partir des apprentissages faits au secondaire, il est possible d'en déduire plusieurs!
Lors d'une discussion, il est important que nos propos soient appuyés par des faits fiables et vérifiables. On apprend, entre autres, à citer des spécialistes, des statistiques, etc.
Il faut aussi s'assurer que nous n'avons pas cherché une information dans le simple but de confirmer notre opinion. Souvent, trouver plusieurs références permet d'éviter le biais de confirmation.
Il faut aussi bien réfléchir à ce qu'on dit. Cela permet d'éviter les faux dilemmes, par exemple. Est-ce qu'une chose x s'oppose nécessairement à une chose y?
Dans le cas où on discute pour convaincre, on peut utiliser des stratégies argumentatives comme l'explication argumentatives.
Au final, bien connaitre les entraves au dialogue (aussi appelés sophismes) permet d'être conscient des biais qu'on peut avoir lors d'une conversation. Ils nous rappellent d'être vigilants! :D
Laurie :)
Re: Question
Bonjour FramboiseAutonome2366,
Merci pour ta question :)
Tu n'auras pas besoin d'utiliser ton rapporteur d'angles dans cet exercice, puisque tu compares des figures semblables.
On dit que 2 figures sont semblables si tous les rapports de côtés homologues sont proportionnels et que tous les angles homologues sont isométriques. Ça signifie qu'il faut tout d'abord que tu identifie les côtés homologues (ceux qui sont proportionnels) et tu pourras déduire que les angles homologues sont congrus :)
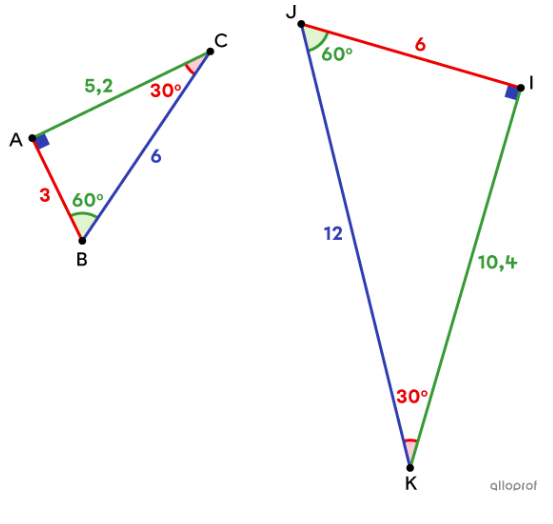
Voici une image qui pourra peut-être t'aider à visualiser:
Tu peux déduire ici (ou peut-être que tu auras besoin de ta règle si ce n'est pas facile à voir) que les côtés de mêmes couleur sont proportionnels. On peut donc en déduire que les angles entre le côté bleu et vert sont homologues dans les deux triangles, et donc congrus :)
N'hésite pas si tu as d'autres questions :)
Sandrine
Tu n'as pas besoin de ton rapporteur d'angle pour cet exercice, puisque cet exercice porte sur les figures semblables
Re: Question
Bonjour!
Afin de répondre à cette question, je te suggère de consulter la fiche ci-dessous :
En ce qui concerne la deuxième question, serait-ce possible pour toi de nous préciser de quelle période il est question? Cela nous aidera à mieux te répondre! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonsoir, RubisIota3608!
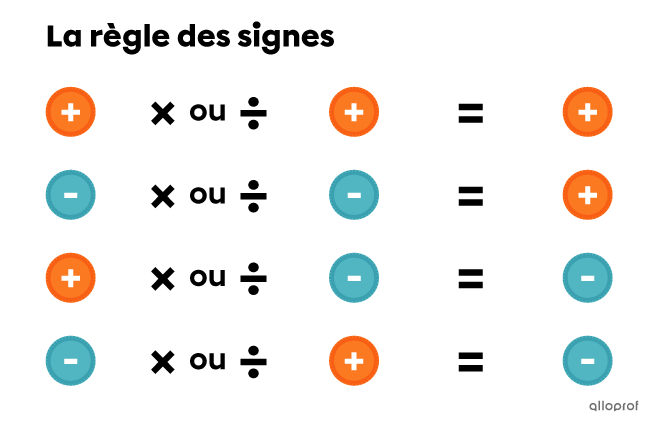
Puisque les deux nombres multipliés sont de signes contraires, le résultat est négatif. Tu peux donc les multiplier sans tenir compte des signes, mais en donnant le résultat final avec le bon.
Tu multiplies des nombres décimaux de la même façon que tu multiplies des nombres entiers.
Tu dois juste compter le nombre de chiffres qui sont après la virgule dans les facteurs pour savoir où placer la virgule dans la réponse.
Par exemple, 2,53 × 3,1 = ?
J’écris la multiplication en colonne.
J’effectue la multiplication sans me soucier des virgules.
Je compte le nombre de chiffres qui sont après la virgule dans les facteurs.
Ce nombre m’indique combien de chiffres mettre après la virgule dans la réponse.
Dans cet exemple, il y a 3 chiffres.
Je place la virgule dans la réponse.
Dans cet exemple, je mets 3 chiffres après la virgule.
2,53 × 3,1 = 7,843
N'hésite pas à poser d'autres questions!
Re: Question
Bonsoir, SauterelleDelta6149!
Merci de ton intérêt pour être pro de la zone d'entraide! Étant en secondaire 4, tu pourrais t'inscrire au bénévolat. La personne responsable communiquera avec toi sous peu via la messagerie de la Zone d’entraide. On a hâte de faire ta connaissance!
Re: Question
Bonjour GalaxieSigma4570,
Merci beaucoup pour ta question! Si tous les chiffres présents dans ton énoncé comportent 3 chiffres significatifs, alors tu dois également mettre 3 chiffres significatifs dans ta table de valeur. En effet, il faut respecter le nombre de chiffres significatifs indiqués et il faut essayer de demeurer le plus précis possible. C’est pourquoi je mettrai 3 chiffres significatifs dans ma table de valeur. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour,
Pour effectuer la transformation demandé, tu dois utilisé les propriétés des logarithmes :
\( a \cdot \log_c(b(x-h)) + k = \)
\(\log_c\left( (b(x-h))^a \right) + k = \)
\(\log_c\left( (b(x-h))^a \right) + k \cdot \log_c(c) = \)
Il est à noter ici que puisque \( \log_c(c) = 1, k * \log_c(c) = k*1 = k\).
\(\log_c\left( (b(x-h))^a \right) + \log_c(c^k) = \)
\(\log_c\left( (b(x-h))^a \cdot c^k \right) = \)
\(\log_c\left( b^a \cdot (x-h)^a \cdot c^k \right) = \)
\(\log_c\left( (b^a \cdot c^k) \cdot (x-h)^a \right) = \)
\(\log_c\left( B(x-h)^a \right) \)
où \(B = b^a \cdot c^k\)
Si tu as d'autres questions n'hésite pas à venir les poser !
Bonne journée :)
Re: Question
Bonjour NickelAlpha325, merci pour ta question !
Je pense avoir compris que tu faisais référence à \(y = a(c)^x + k\) pour les fonction exponentielle ?
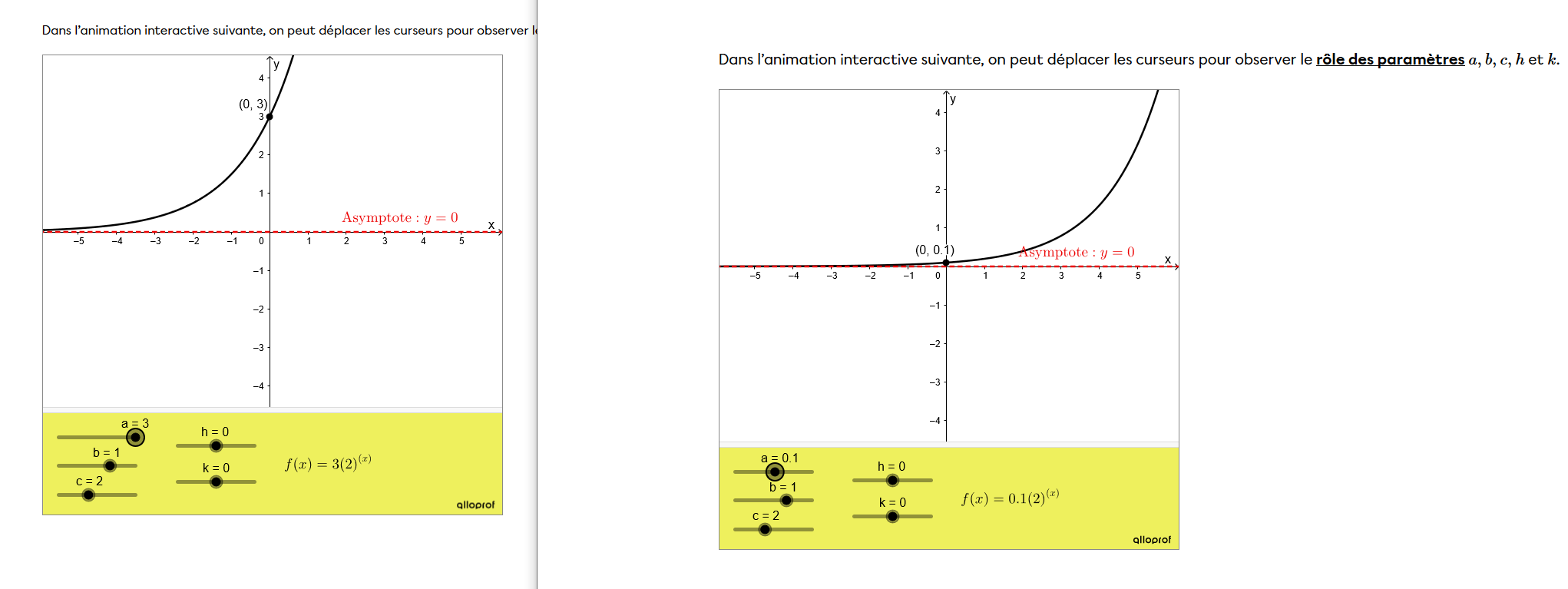
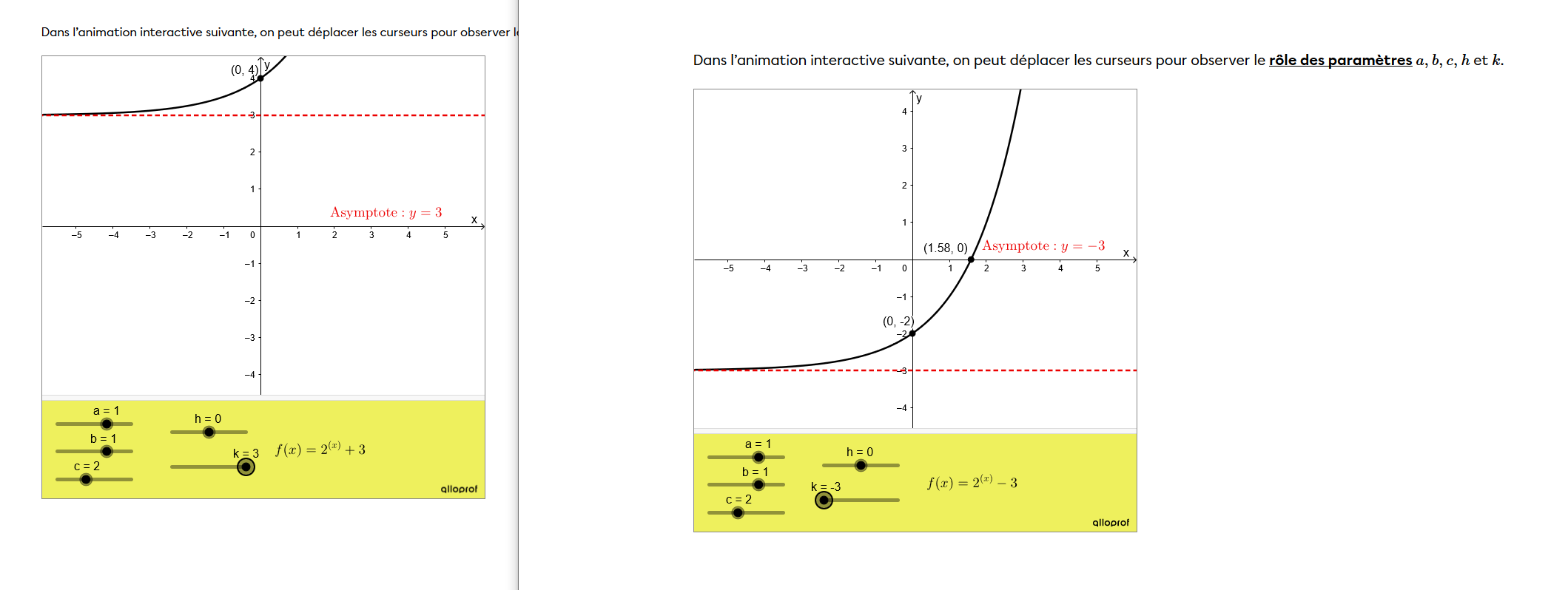
Le paramètre "a" sert à déterminer si ta courbe va augmenter plus ou moins vite, c'est comme le coefficient directeur des fonctions affines.
Dans cet exemple, je modifie le paramètre "a" la courbe augmente plus ou moins vite, et elle sera décroissante si le paramètre est négatif.
Le "k" définit le point de départ de ta courbe. Elle agit donc comme l'ordonnée à l'origine (qui serait de 10 bactéries dans ton exemple).
Tu peux en savoir plus et utiliser ce simulateur ici : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-fonction-exponentielle-m1143
N'hésite pas à nous écrire si tu as d'autres questions !