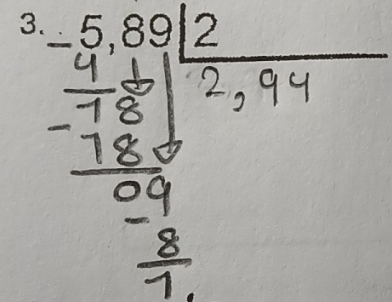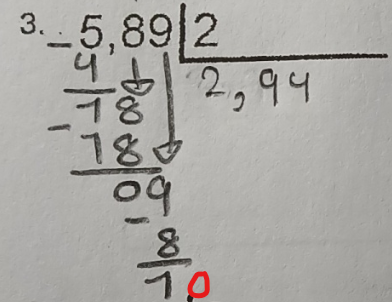Best Of

Salut!

Tout d'abord, voici mes corrections :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tes réponses sont toutes les bonnes, mais il manque quelques chiffres après la virgule pour plusieurs.

En fait, lorsque tu fais une division, tu peux obtenir trois types de résultats :

1. En nombre décimal avec un certain nombre de chiffres après la virgule (ex. 94,37)
2. Un nombre décimal avec une infinité de chiffres après la virgule, et ces chiffres sont aléatoires (ex. 3,19879834782....)
3. Un nombre décimal avec un nombre de chiffres infini après la virgule, mais il s'agit du même chiffre ou de la même séquence de chiffre qui se répète (ex. 5,2222222222...). On appelle ces nombres des nombres périodiques.

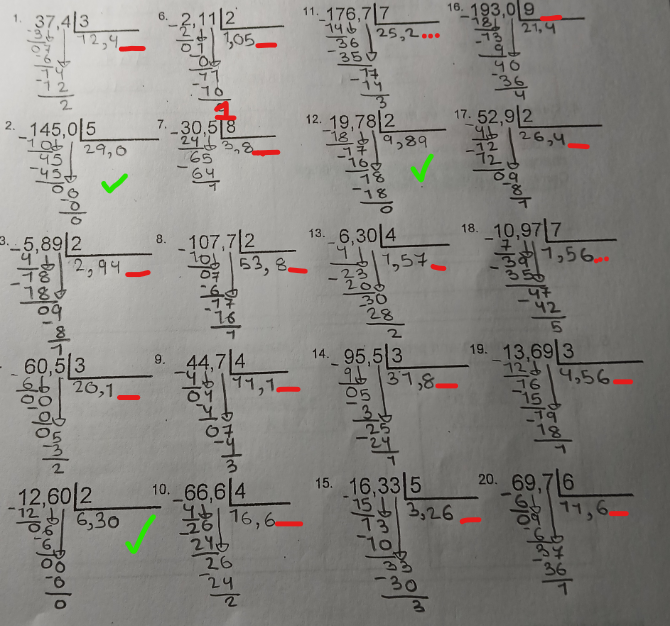
Ainsi, pour résoudre ces divisions, voici comment je te propose de fonctionner: tu commences par effectuer ta division comme à l'habitude. Lorsque tu es rendu à diviser des chiffres qui sont dans la partie décimale du nombre, si tu obtiens un reste de 0, alors tu as fini ta division, et cela signifie que tu as obtenu un résultat avec un nombre de chiffres précis après la virgule (type #1). Si tu n'as pas un reste de 0, tu continues la division, et ce, en ajoutant un 0 à ton reste. Par exemple, ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On a un reste de 1. Nous allons donc ajouter un 0 à droite de ce 1 :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On peut ainsi diviser notre reste de 10 par 2, ce qui nous donne 5. On constate alors qu'on n'a plus de reste, donc la division est maintenant terminée!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La réponse est donc 2,945.

Si on avait encore eu un reste, alors il aurait fallu rajouter un autre 0. Il faut faire cela à chaque fois que l'on a un reste.

Maintenant, le problème, c'est que certains nombres possèdent un nombre infini de chiffres après la virgule. Bien sûr, on ne va pas continuer la division indéfiniment 😆. Si on voit qu'on est rendu à 3 ou 4 chiffres après la virgule et qu'on a toujours un reste, on peut s'arrêter là et conclure qu'on a un nombre du type 2 dont je te parlais précédemment, c'est-à-dire un nombre avec un nombre infini de chiffres aléatoires après la virgule. Pour écrire ce nombre, tu peux mettre trois petits points à la fin pour montrer qu'il continue jusqu'à l'infini (ex. 3,492...).

Cependant, si on constate qu'on obtient le même chiffre plusieurs fois de suite, alors on conclut qu'il s'agit d'un nombre périodique (type 3), et donc on peut mettre une petite barre en haut du chiffre qui se répète (ex. 4,66666 = \(4,\overline{6}\)).

Je te laisse corriger le tout avec ces indices. Reviens nous voir si tu as besoin d'aide! :)

Salut!

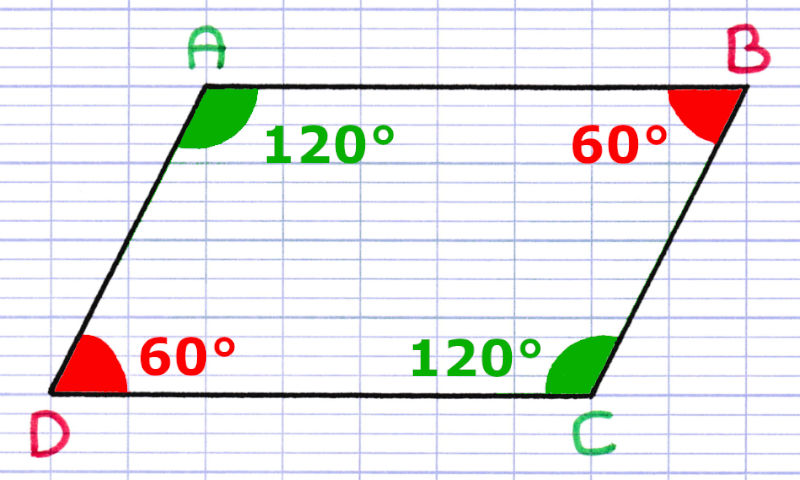
Un angle consécutif à un autre est un angle qui a un côté du polygone en commun. En d'autres mots, ce sont des angles "voisins".

Par exemple, l'angle A et l'angle B sont consécutifs, puisqu'il partage le côté AB. Cependant, l'angle A n'est pas consécutif à l'angle C, puisqu'ils ne partagent aucun côté en commun. L'angle A est également consécutif à l'angle D. Ainsi, l'angle A a pour angle consécutif les angles qui lui sont voisins, soit A et B.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici des explications supplémentaires qui pourraient t'intéresser :

• Bonjour, je ne comprends toujours pas ce qu'est un angle con — Alloprof
• Bonjour, <br> Quelle est un angle consécutif et quelle est une — Alloprof

J'espère que c'est plus clair pour toi! :)

Salut!

Des figures équivalentes sont des figures qui ont la même aire. Cependant, dans cet exercice, on ne dit pas que les figures sont équivalentes, mais plutôt que les périmètres sont équivalents, ce qui signifie que le rectangle et le triangle possèdent le même périmètre. Ainsi, en trouvant le périmètre d'une des figures, tu trouveras également le périmètre de l'autre figure.

Tu peux commencer par calculer le périmètre du rectangle. Ensuite, tu peux t'en servir pour trouver les deux mesures isométriques manquantes du triangle.

Pour trouver l'aire du triangle avec la mesure de ses côtés, tu peux utiliser la formule de Héron, ou le théorème de Pythagore pour trouver la mesure de la hauteur, et ensuite calculer l'aire avec la formule d'aire d'un triangle.

Je te laisse essayer avec ces indices. Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Tu as bien commencé.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu cherches la différence entre 60cm (la première mesure du pied du mur au point C) et x (la deuxième mesure du pied du mur au point C).

Bonjour, pour résoudre ce problème, tu dois trouver la mersure du côté BC. Pour ce faire, tu doit trouver la mesure du côté BP en utilisant la relation de pythagore. Ensuite, tu devras enlever 61 cm de la mesure du côté BP que tu avait calculé auparavant. Pour trouver la solution, tu devras réutiliser la relation de pythagore avec ta nouvelle mesure BP en appliquant la relation à l'envers : C au carré = A au carré + B au carré.

Bonjour LynxSupra1006,

Merci d'utiliser la zone d'entraide pour te venir en aide.

C'est tout à fait normal d'avoir un peu de difficulté avec les expériences aléatoires, je vais donc un peu t'aider.

D'abord, je penses que cette fiche Alloprof pourra t'aider avec les diagrammes en arbres

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-diagramme-en-arbre-m1360

D'ailleurs, il y a 2 types de diagrammes en arbres. Ceux qui permettent de trouver les possibilités, et ceux qui permettent de calculer la probabilités de résultats.

Je te conseillerais également de vérifier le contexte et des bien lire les énoncés. De plus, n'oublie pas de vérifier si l'expérience est avec ou sans remise.

Si tu as d'autres questions, n'hésite pas à revenir poser des questions !

Bon travail,

OnyxIntergalactique1301

Note that you should not confuse the volume of the reservoir which is a cube containing liquid plastic with the smaller cube to be made from the plastic in the reservoir.

Le volume du réservoir de plastique liquide est de (1.83m)³= (1.83cm)³= 6 128 487 cm³

et génère 3 375 solides de même volume

Donc le volume d'un solide sera de

6 128 487 cm³/3 375 = 1815.85 cm³

Ce que tu as trouvé, Bravo!

Les 5 solides décrit dans l'énoncé ont 1815.85 cm³ de volume.

Tu sais qu'un cube de côté c a un volume de c³ tu peux donc déterminer le c du cube à modeler, le c est aussi la hauteur du cube.

Cette hauteur est aussi celle du cylindre, de la pyramide carrée et du cône.

Va voir cette page qui donne le volume de différents solides en fonction de leurs mesures: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-et-le-volume-des-solides-m1243

Je te laisse trouver les dimensions des divers solides.