Best Of
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Les chats ont en effet un odorat très développé, 40 fois plus puissant que celui des hommes!
Pour en savoir plus, je te propose de lire la référence suivante:
À bientôt,
Karen
Re: Question
Salut!
Non, la Zone d'entraide est complètement gratuite 😋. Alloprof est là pour t’aider dans tes études sans frais, donc n’hésite pas si tu as des questions, on est là pour toi! 😁
Re: Question
Salut,
L'impératif présent est un temps de verbe exprimant un ordre ou une nécessité. Contrairement aux autres temps de verbe, il se conjugue sans pronom et seulement à trois personne :
- 2e personne du singulier (tu)
- 1 ere personne du pluriel (nous)
- 2e personne du pluriel (vous)
Voici les terminaisons générales de l'impératif, les retenir t'aidera assurément :
***Attention !!! Comme tu peux le remarquer, la terminaison de la 2e personne du singulier des verbes du premier groupe (er) ne prend pas de s !
Pour en savoir plus sur l'impératif, c'est juste ici :
Pssst ! Savais-tu que nous avons une fiche par temps de verbe ? Pour les trouver, tu n'as qu'à utiliser l'onglet recherche, en sélectionnant «français» et «fiche». Tu n'auras qu'à écrire le nom du temps de verbe que tu souhaites étudier ! :D
À la prochaine !
Karen
Re: Question
Salut,
Merci d'utiliser nos services!
Nous travaillons toujours fort pour créer de nouveaux jeux, je t'invite à rester à l'affût!
Tu peux nous transmettre ta suggestion en cliquant sur ce lien:
À bientôt,
Karen
Re: Question
Salut!
Nos termes sont 3, 6, 11 et 20. Regardons de plus près les différences entre les termes :
De 3 à 6, on ajoute 3.
De 6 à 11, on ajoute 5.
De 11 à 20, on ajoute 9.
Est-ce que tu remarques quelque chose avec ces additions (3, 5, 9)? Elles ne sont pas constantes, mais elles semblent augmenter… On passe de +3 à +5, donc notre bond augmente de 2. Ensuite, on passe de +5 à +9, donc notre bond augmente de 4.
Ainsi, si on suit cette tendance, notre prochain bond devrait augmenter de 6, donc, on doit ajouter 9+6=15 à notre nombre précédent, soit 20.
Cependant, je ne peux pas te garantir à 100% que cette suite suit cette logique, à moins d’avoir plus d’infos. Ainsi, pourrais-tu nous envoyer une photo de l'exercice? Cela nous aiderait à mieux te guider si l'on a tout le contexte de l'exercice :)
J'espère que cela t'aide! À bientôt! :)
Re: Question
Salut DiamantTurbo988 😁
Merci pour ta question!
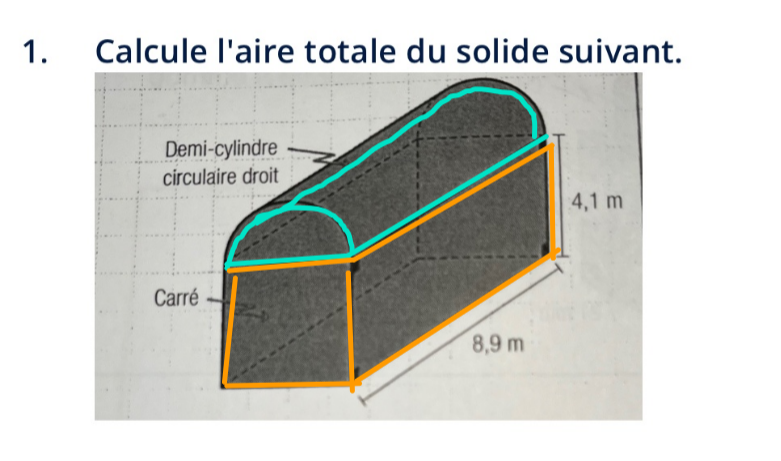
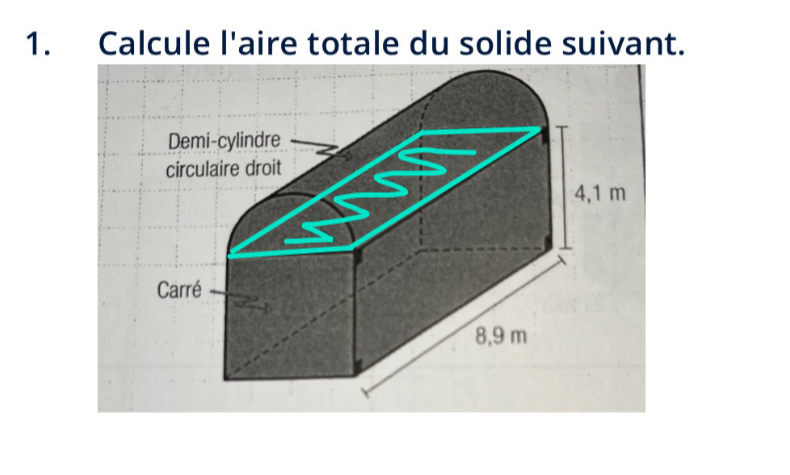
Certainement, prenons le numéro 1 en exemple.
Il faut d'abord repérer les différents solides. Ici, on a un demi-cylindre et un prisme rectangulaire à base carrée.
Pour réviser les solides et leur nom, c'est par ici.
Ensuite, il y a deux manières de faire.
1) On prend les formules d'aire totale des deux solides, puis on y soustrait les faces qu'on ne voit pas de l'extérieur (celles qui collent les deux solides ensemble), en d'autres mots, celles auxquelles on n'aurait pas accès si on trempait la forme dans la peinture.
2) On calcule l'aire des faces qu'on voit.
Il y aurait 2 demi-cercles, une demie-aire latérale pour le cylindre, deux faces carrées, trois faces rectangulaires.
Les deux démarches mènent à la même réponse, dans une, on fait une ou des soustractions, dans l'autre, une ou des additions.
Toutes les formules se trouvent ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
C'est gentil de prendre le temps de nous faire cette suggestion, nous travaillons toujours fort pour créer du nouveau matériel et de nouveaux jeux pour vous.
Reste à l'affût.
N'hésite pas à communiquer directement avec notre équipe de création en utilisant ce lien:
À bientôt,
Karen
Re: Question
Bonjour AbafarAgile2197,
Merci pour ta question :)
Les exercices que tu as envoyés sont des exercices de dilution. La dilution est un procédé utilisé pour diminuer la concentration d’une solution en y ajoutant du solvant sans changer la quantité de soluté. La formule dont tu as besoin pour calculer des dilutions est:
Une chose qui est importante à noter est que les unités sont constantes dans la formule pour la concentration ainsi que pour le volume. Ça signifie que tes deux variables de volume V1 et V2 doivent être dans les mêmes unités (donc toutes les deux en mL ou en L par exemple) et que tes variables de concentration sont aussi dans la même unité (donc si tu fais un calcul avec une concentration en %, l'autre concentration dans ta formule devra aussi être en pourcentage).
Le plus difficile dans ces exercices est d'identifier ce qu'est C1, V1, C2 et V2. Prenons l'exemple de l'exercice 16. La solution de départ est une solution de 250 mL avec une concentration de 33% (v/v). On peut donc dire que C1=33% et V1=250 mL. On ajoute 500 mL d'eau. On sait donc que la solution finale aura un volume de V2=750 mL (250+500), mais on ne connait pas sa concentration C2=?
On peut donc utiliser la formule précédente pour calculer: 33% x 250 mL = C2 x 750 mL. En isolant C2, je trouve que sa valeur est de 11%.
Dans ton problème 17, cette fois-ci tu connais les informations de la solution de départ, et tu connais la concentration de la solution finale 9C2=40 g/L puisque c'est la concentration que tu souhaites obtenir). Avec la formule, tu pourras trouver le volume final de la solution. Attention cependant, on cherche le volume d'eau à ajouter, donc le volume d'eau qu'on ajouté pour passer du volume initial au volume final :)
Si tu veux te pratiquer encore, je t'invite à consulter cette page: https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-dilution-c1v1-c2v2-s1054
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Hi!
I'm not sure what your question is. Do you need some help with capitalization in English? If so, I suggest you read this factsheet :
Laurie :)