Best Of
Re: Question
ccq ça veut dire culture et citoyenneté québécoise
tu vas apprendre comment vivre respectueusement selon les valeurs et différente culture
Re: Question
CCQ veut dire Culture et Citoyenneté Québécoise
Ça a remplacé ECR
Re: Question
Bonjour MarsHonorable4165!
L'abréviation "CCQ" veut dire culture et citoyenneté québécoise ! Ce programme à remplacer le programme éthique et culture religieuse ! J'espère t'avoir aidé !
Bye et bonne journée!!!
-melonfantastique5282🎀🎀🎀
Re: Question
Bonjour MarsHonorable4165,
"CCQ" veut dire "Culture et Citoyennetée Québécoise".
J'espère t'avoir aidé! :D
-CentaureMauve
Re: Question
Salut OnyxAgile3246 😁
Merci pour ta question!
C'est par ici!
Les fractions
Les nombres décimaux
Si tu souhaites jeter un coup d’œil au notions vues en secondaire 1 en maths, c'est par là.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
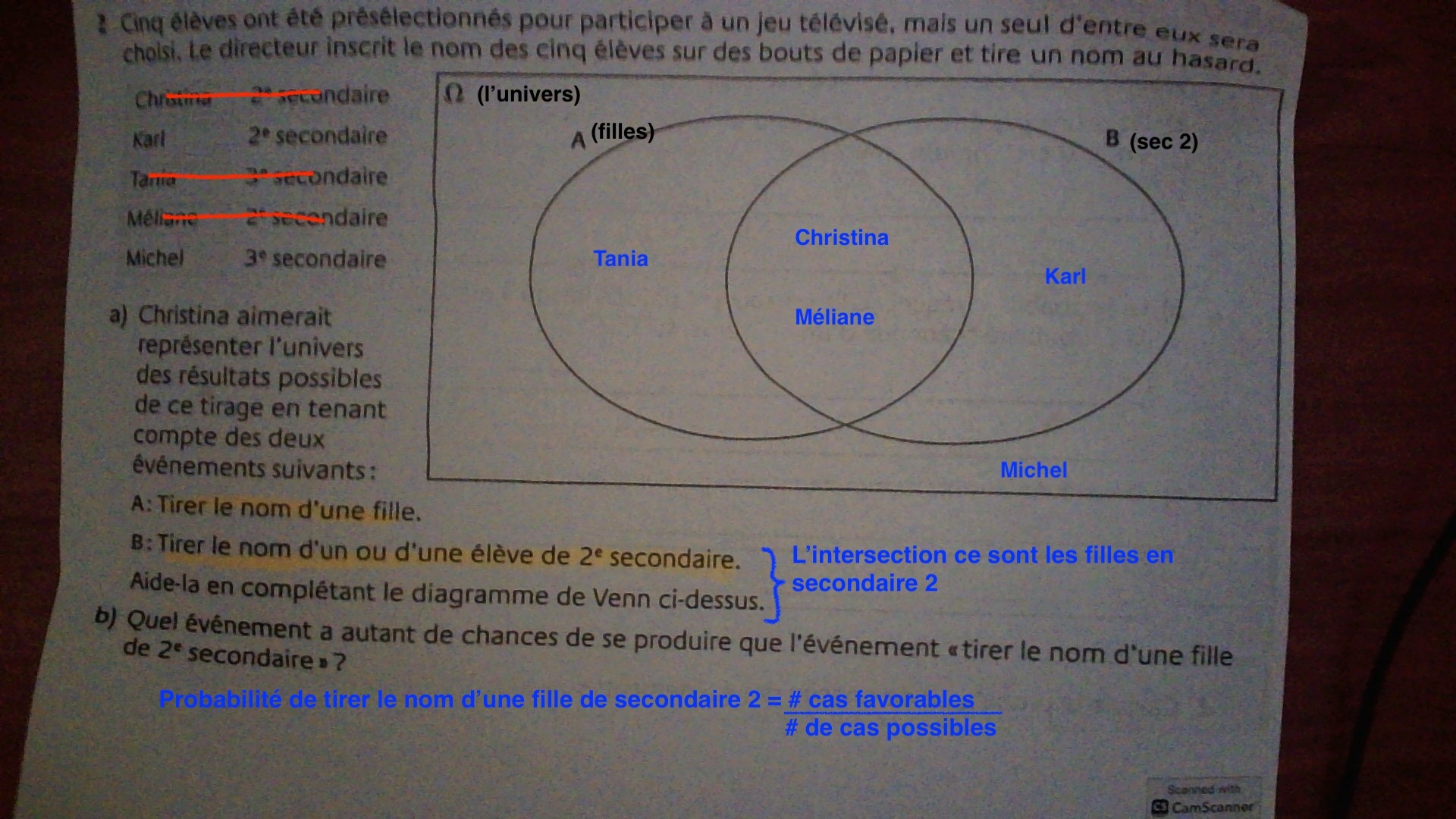
- tu dois d'abord déterminer le contenu de chaque ensemble de ton univers
- ici l'univers, ce sont les 5 élèves présélectionnés
- ensuite tu dois déterminer les chances de tirer le nom d'une fille de secondaire 2 (la probabilité)
- quel autre événement a la même probabilité?
Re: Question
Bonjour,
Merci pour ta question!
Si je comprends bien ce que tu veux dire, tu parles de l'électricité statique. Cette dernière correspond aux phénomènes causés par les charges aux repos. Généralement, les objets sont neutres, donc possèdent autant de charges positives que négatives. Cependant, il existe différentes méthodes pour charger un objet, soit par conduction, par frottement ou par induction. Un objet peut perdre des électrons et devenir chargé positivement, ou il peut en gagner et devenir chargé négativement.
Voici une fiche explicative qui pourrait t'aider à ce sujet :
Elle explique en détail comment un objet peut devenir chargé. De plus, elle contient une vidéo qui pourrait t'être utile.
J'espère t'avoir aidé. N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour!
Il existe plusieurs procédés qui servent à former des mots! :D
Pour les connaître, je te suggère de consulter les fiches ci-dessous. Elles expliquent les différents procédés de formation des mots.
La composition :
La dérivation :
Le télescopage :
L'abrègement :
Pour savoir ce que sont les mots génériques et spécifiques, je te suggère de consulter la fiche ci-dessous :
Dans la fiche ci-dessous, tu trouveras un tableau qui liste les différents préfixes et qui donne leur sens! :D
Tu retrouveras la même chose ici pour les suffixes! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut, je pense que ce que tu veux dire par là c'est que le jeu est vraiment bon haha.
Merci pour ce commentaire, ça nous fait plaisir :)
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Si les reins cessent de filtrer le sel, il peut y avoir plusieurs impacts sur la santé, par exemple de la rétention d'eau, une augmentation de la pression artérielle, de la fatigue, des crampes musculaires, des problèmes cardiaques et des problèmes rénaux. Le rôle des reins est donc essentiel.
Pour en savoir plus sur le maintien de l'équilibre sanguin, je te propose de consulter la fiche suivante:
N'hésite pas à revenir nous voir si tu as d'autres questions.
Bonne journée,
Karen