Best Of
Re: Question
Salut !
Il te faut comprendre qu'au début de l'expérience, avant d'ajouter les poids, le gaz à l'intérieur à une pression en équilibre avec le milieu. Il a donc une pression équivalente à la pression atmosphérique.
En ajoutant de la pression à cette pression atmosphérique, tu diminues le volume de la seringue, mais le produit reste constant.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
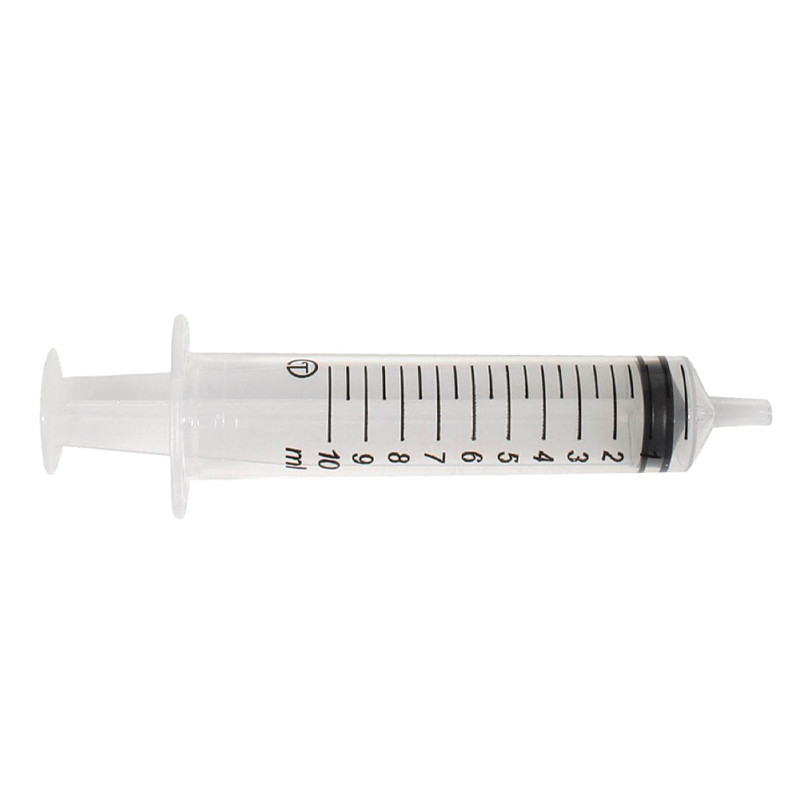
Cela va dépendre de la seringue. L'incertitude de lecture associée à un instrument de mesure analogique correspond à la moitié de la plus petite graduation de l'instrument.
Prenons cette seringue comme exemple.
La graduation est de 0,5. Ainsi, l'incertitude est de \(\pm0,25\).
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Bonjour,
Je t'invite à regarder l'explication que j'ai donnée à ce sujet :
Bonne journée :)
Re: Question
Salut !
La meilleur façon d'identifier un gaz est en effet de calculer sa masse molaire.
$$ PV=nRT $$
$$ V=\frac{MmRT}{P} $$
Si le volume est équivalent entre les bonbonnes, tu as :
$$ V_1=V_2 $$
$$ \frac{M_1m_1RT}{P}=\frac{M_2m_2RT}{P} $$
L'exercice semble toutefois manquer de contexte et d'information. Je t'invite à compléter au besoin. Si on veut aussi inclure le volume, on sait que la pression et la température seraient constantes.
$$ \frac{V_1}{n_1}=\frac{V_2}{n_2} $$
$$ \frac{V_1}{M_1m_1}=\frac{V_2}{M_2m_2} $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Allo CyborgIntergalactique1409,
Merci pour ta question!
Tu peux aller dans la section ''mes question'' sur ton profil alloprof! Si tu les as toutes posées avec le même profil, tu devrais pouvoir les retrouver!
J'espère t'avoir aidé!
Lea-Kim
Re: Question
Salut RubisKappa8548 😁
Merci pour ta question!
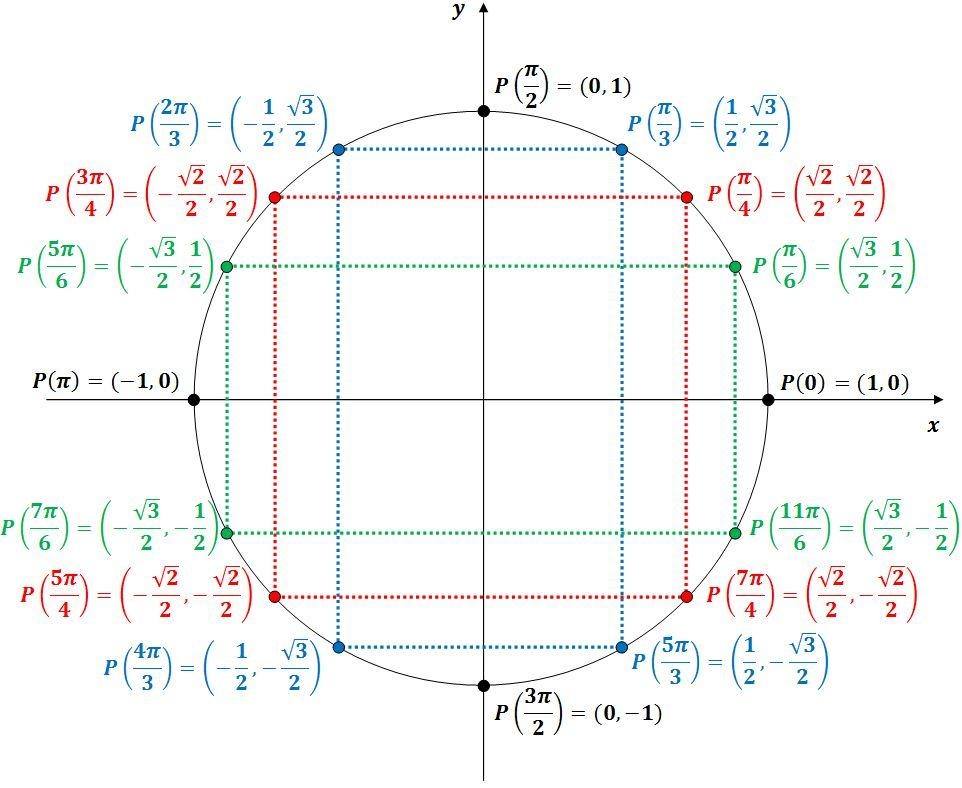
De 0 à 2π signifie pour un tour complet du cercle.
Pour le a), cosecθ représente (1/sinθ). Alors, tu dois trouver les points où 1/la coordonnée x donne 2. Donc, la coordonnée x devra être de 0,5 (1/2). Il y a deux endroits! Je te laisse les trouver.
Pour réviser les identités trigos, c'est par là.
Pour le b), tu dois voir quel point du cercle a pour ordonnée (y) 0. Il y a aussi deux endroits!
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Allo ScorpionGrandiose9713,
Merci pour ta question!
Les nombre décimaux sont des nombres à virgule. Ils ne sont pas entiers. Il y a une partie entière et une partie décimales séparé par une virgule.
Nous avons une fiche pour plus d'informations!
J'espère t'avoir aidé!
Lea-Kim
Re: Question
Salut PommeJuste3931!
Merci pour ta question. :)
Oui, tout à fait! Si cela apporte un "effet" à ton poème, tu peux parfaitement enfreindre toutes règles de ponctuation.
En ce qui a trait aux règles de ponctuation pour la poésie de forme libre, tu n'es pas la seule personne qui se questionne sur le sujet! Je t'invite donc à consulter la super explication qui a été donnée à cette question semblable à la tienne. :D
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Bonjour, AnanasJaune817!
1) Tracer une image sur un miroir plan
Étapes :
- Dessiner le miroir : Trace une ligne droite pour représenter la surface réfléchissante du miroir. Indique quel côté est réfléchissant.
- Placer l’objet : Place un point ou une figure quelconque devant le miroir (par exemple, une flèche ou un objet comme une boule).
- Trouver la position de l'image :
- L'image d'un objet dans un miroir plan se trouve à la même distance derrière le miroir que l'objet est placé devant celui-ci.
- Mesure la distance entre l'objet et le miroir. Trace cette même distance de l’autre côté du miroir. Cela te donne la position de l'image.
- Dessiner l’image :
- Reproduis exactement la même forme que l'objet, mais inversée latéralement (la gauche devient la droite et vice versa).
- Tracé des rayons lumineux :
- Dessine deux rayons lumineux partant de l’objet vers le miroir. Ces rayons doivent refléter dans le miroir en respectant la loi de réflexion : Angle d’incidence=Angle de reˊflexion\text{Angle d'incidence} = \text{Angle de réflexion}Angle d’incidence=Angle de reˊflexion
- Prolonge les rayons réfléchis derrière le miroir avec des lignes pointillées pour montrer où se forme l’image.
2) Localiser les images de l'autre côté d'un miroir
Étapes :
- Observer les points-clés :
- Chaque partie de l'image d'un objet se trouve directement en face de l'objet, à une distance équivalente de l'autre côté du miroir.
- Dessiner plusieurs points :
- Si l'objet est une flèche, prends plusieurs points caractéristiques (comme la base et le sommet). Mesure leurs distances au miroir et reporte ces distances de l'autre côté.
- Relier les points :
- Une fois que tu as reporté tous les points, relie-les pour former l'image complète.
- Astuce pour valider :
- Vérifie que toutes les distances sont cohérentes et que l'image est bien symétrique par rapport au miroir.
Exemple simple :
Si tu as une flèche de 5 cm placée à 3 cm devant un miroir :
- Trace une ligne droite pour le miroir.
- Mesure 3 cm derrière le miroir et place une flèche inversée latéralement.
- La distance entre la flèche et son image sera de 6 cm (3 cm devant + 3 cm derrière).
Si tu as un croquis à faire et que tu n’es pas sûr de l’exactitude, n’hésite pas à partager ou poser d'autres questions pour éclaircir. Bonne chance pour ton devoir ! 😊
Re: Question
Allo TortueEnthousiaste5928,
Merci pour ta question!
Pour résoudre une équation algébrique, tu dois toujours regrouper les x ensemble et les nombres ensembles. De cette façon, tu peux trouver la valeur de x. Lorsqu'il y a des fractions, on les traite comme des nombres. N'oublie pas que l'addition et la soustraction sont des opérations inverses comme la multiplication et la division.
C'était mes petits trucs. Pour des exemples, je te conseille de consulter la fiche suivante:
Elle contient plusieurs méthodes! Tu pourras choisir ta favorite!
J'espère t'avoir aidé!
Lea-Kim