Bonjour!
Merci pour votre explication, mais je pense ne pas toujours avoir compris.
Désolée, mais je n'ai toujours pas capté comment arriver à prouver que les angles de ce losange sont différents de 90 degrés (ce qui prouve qu'il ne s'agit pas d'un carré, malgré que ses quatre côtés mesurent la même chose).
J'avais demandé de l'aide pour :
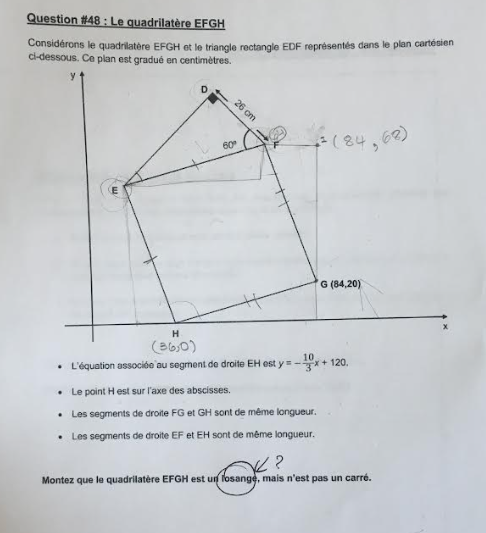
1) Pour trouver la distance EH (et comment trouver les coordonnées du point D, E et F)
2) Trouver un moyen de prouver que les angles consécutifs sont supplémentaires OU trouver la mesure de chaque angle.
Je vous insère encore en pièce-jointe le problème, ainsi que mes calculs :)
Merci et j'espère que vous comprenez un peu mieux ce que je veux comprendre. :D J'aurais un comme ceci dans mon blocage horaire.
Désolée encore une fois pour l'inconvénience :)

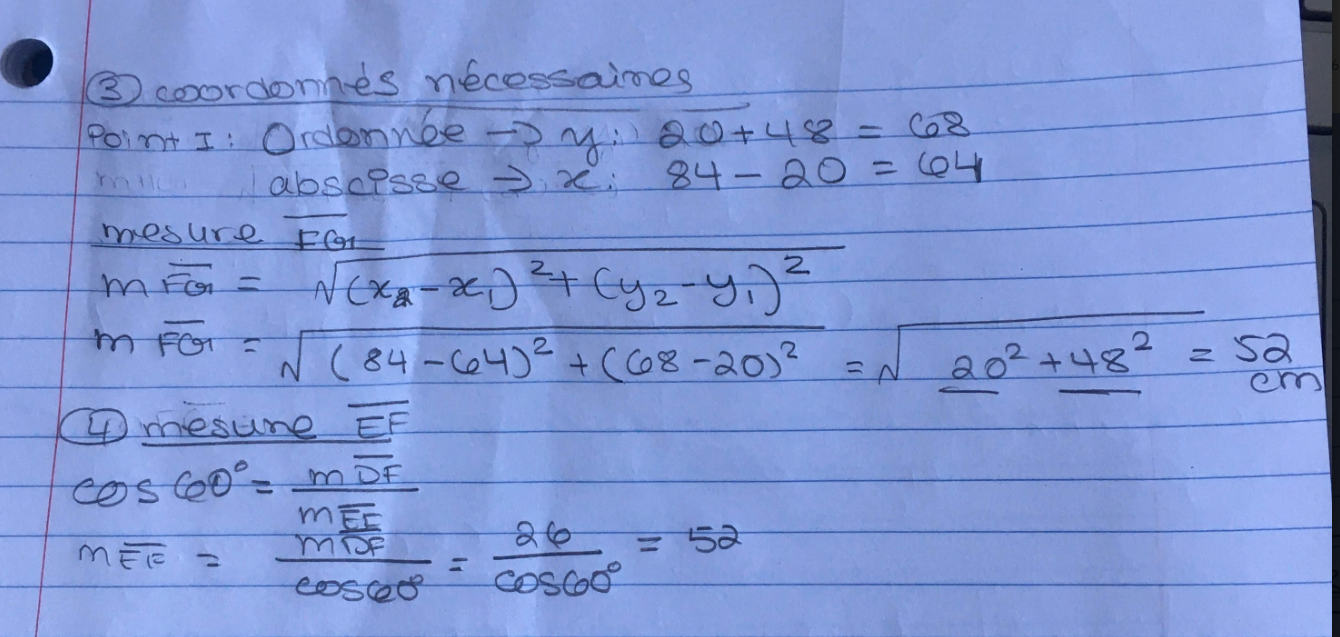






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut !
Merci de faire appel de nouveau au service d'Alloprof ! Allons-y un point à la fois.
1) Valeur de EH
Il semble que tu ais déjà trouvé les coordonnées de H et F et celle de G a été donnée. Comme indiqué dans l'énoncé, la valeur de EH est la même que celle de EF. Il te suffit donc de trouver la valeur de EF. Pour ce faire, tu peux utiliser la relation cosinus de l'angle 60 degrés dans le triangle DEF. Tu sembles avoir compris cette partie.
Avec cela, tu auras toutes le mesure du quadrilatère. Tu peux donc déduire qu'il s'agit de soit un losange ou un carré.
Pour trouver les coordonnées de E, tu peux le faire en trouvant le croisement entre les droite EF et EH. Tu as déjà la règle de EH. Il te faut la règle de EF. Pour ce faire, tu sais que les mesures GH et EF sont parallèle, qu'il s'agisse d'un losange ou d'un carré.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ainsi la pente de la droite qui décris GH (que tu peux calculer) est la même que celle de EF. Avec cette pente et le point F, tu peux trouver la règle de la droite EF.
Finalement, tu peux peux trouver le croisement entre EF et EH pour calculer les coordonnées de E.
2) Prouver qu'il ne s'agit pas d'un carré, tu n'as qu'à prouver que les distances des diagonales EG et HF ne sont pas isométriques.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !