Matières
Niveaux
Les quadrilatères
Fiche | Mathématiques
Secondaire
1-2
Les quadrilatères sont des polygones formés par une ligne brisée fermée ayant 4 côtés.
Il existe plusieurs classes de quadrilatères. Pour les distinguer, on analyse les mesures des côtés, les mesures des angles et la position relative des côtés.
Les classes de quadrilatères
Voici un diagramme qui illustre les relations entre les familles de quadrilatères.
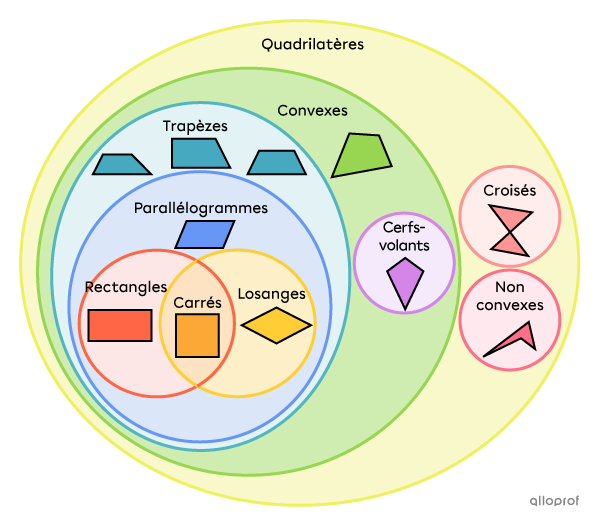
Dans ce diagramme, on peut distinguer 3 grandes classes de quadrilatères : croisés, non convexes et convexes.
Les polygones convexes se trouvant au centre du diagramme possèdent plus de caractéristiques.
Un quadrilatère convexe est un trapèze s’il a 1 paire de côtés parallèles.
Un trapèze qui a 2 paires de côtés parallèles est un parallélogramme.
Un parallélogramme dont les 4 côtés sont isométriques est un losange, tandis qu’un parallélogramme qui a 4 angles droits est un rectangle.
Finalement, un carré est à la fois un rectangle et un losange.
Résumé des propriétés
L’image ci-dessous est ce qu’on appelle un arbre décisionnel qui permet d’identifier un quadrilatère en fonction de ses caractéristiques.
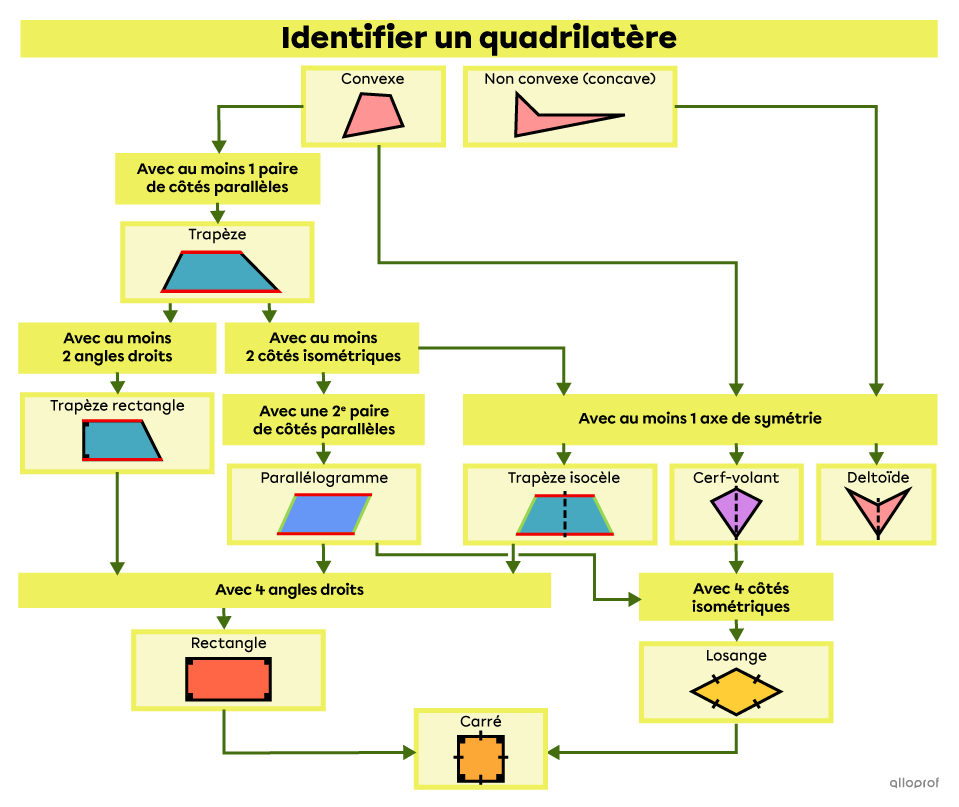
Voici un tableau résumé qui présente les propriétés des différents quadrilatères.
Le cerf-volant
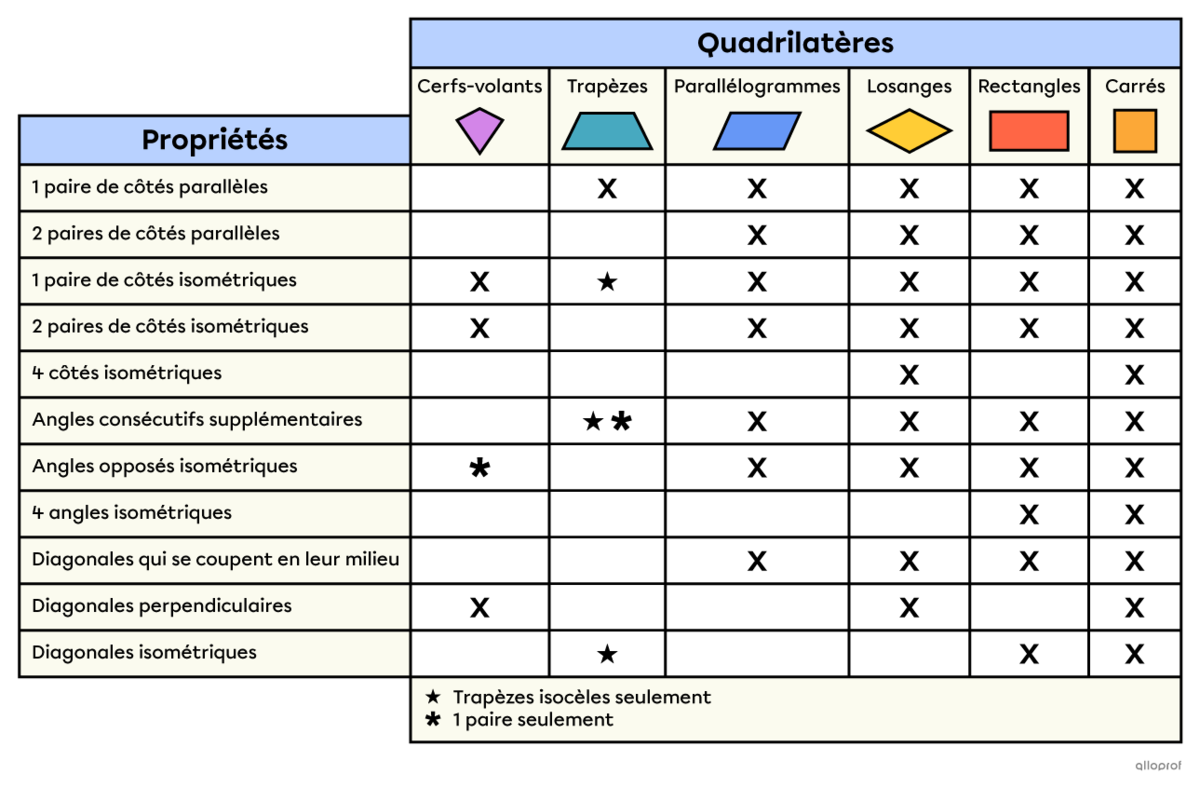
Un cerf-volant est un quadrilatère convexe ayant 2 paires de côtés adjacents isométriques.
Le cerf-volant possède plusieurs propriétés :
-
il a 1 paire d'angles opposés isométriques;
-
ses diagonales sont perpendiculaires.
Définition
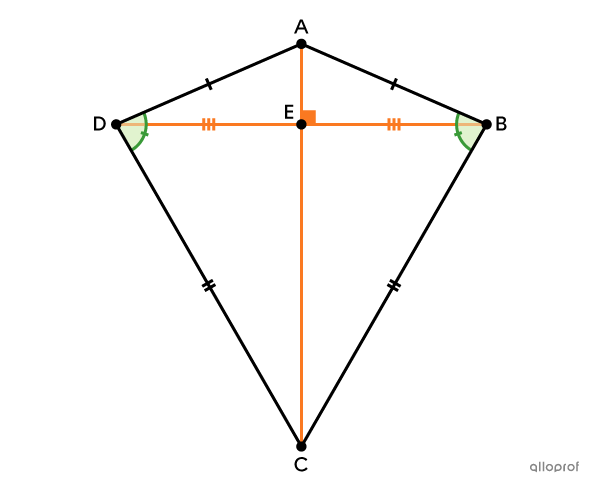
Il a 2 paires de côtés adjacents isométriques.||\begin{align}\overline{AB} &\cong \overline{AD}\\\overline{BC} &\cong \overline{CD}\end{align}||
Propriétés
Il a 1 paire d’angles opposés isométriques.||\angle{ABC}\cong\angle{ADC}||
Les diagonales sont perpendiculaires.||\overline{AC}\perp\overline{BD}||
Le trapèze
Un trapèze est un quadrilatère convexe ayant au moins 1 paire de côtés parallèles.
Définition
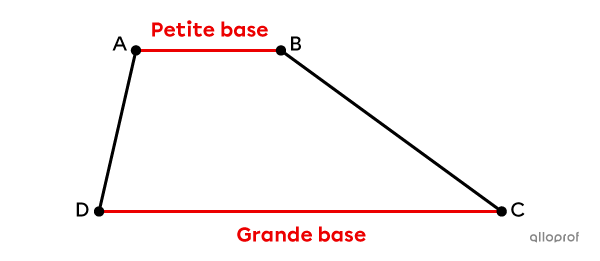
Il a 1 paire de côtés parallèles.||\overline{AB} \parallel \overline{CD}||
Le trapèze rectangle
Un trapèze rectangle est un trapèze ayant au moins 2 angles droits.
Définition
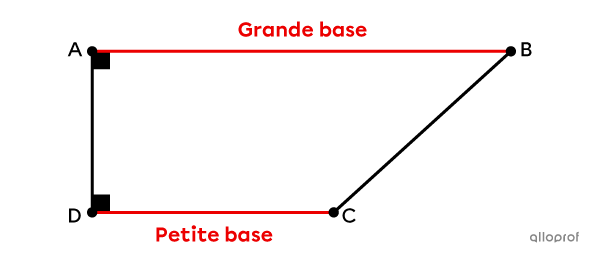
Il a 1 paire de côtés parallèles.||\overline{AB} \parallel \overline{CD}||
Il a 2 angles droits.||\begin{align}\text{m}\angle{DAB}&=90^\circ\\ \text{m}\angle{ADC}&=90^\circ\end{align}||
Le trapèze isocèle
Un trapèze isocèle est un trapèze dont les 2 côtés non parallèles sont isométriques.
Le trapèze isocèle possède plusieurs propriétés :
-
il a 2 paires d’angles consécutifs supplémentaires;
-
il a 2 paires d’angles consécutifs isométriques;
-
il a des diagonales isométriques.
Définition
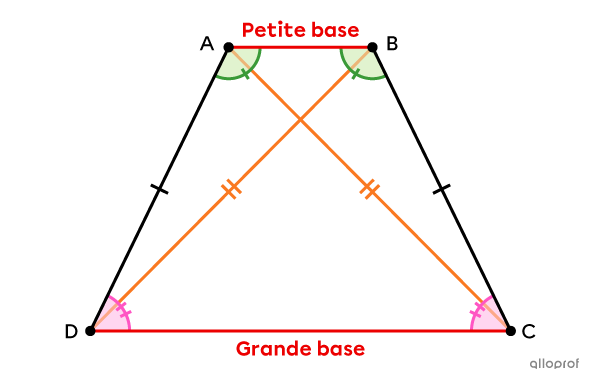
Il a 1 paire de côtés parallèles.||\overline{AB} \parallel \overline{CD}||
Il a 1 paire de côtés isométriques.||\overline{AD}\ \cong\ \overline{BC}||
Propriétés
Il a 2 paires d’angles consécutifs supplémentaires.||\begin{align}\text{m}\angle{BAD}+\text{m}\angle{ADC}&=180^\circ\\ \text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\end{align}||
Il a 2 paires d’angles consécutifs isométriques.||\begin{align}\angle{BAD}&\cong\angle{ABC}\\ \angle{ADC}&\cong\angle{BCD}\end{align}||
Les diagonales sont isométriques.||\overline{AC}\cong\overline{BD}||
Le parallélogramme
Un parallélogramme est un quadrilatère convexe dont les 2 paires de côtés opposés sont parallèles.
Le parallélogramme possède plusieurs propriétés :
-
il a des angles opposés isométriques;
-
il a des angles consécutifs supplémentaires;
-
ses côtés opposés sont isométriques;
-
ses diagonales se coupent en leur milieu.
Définition
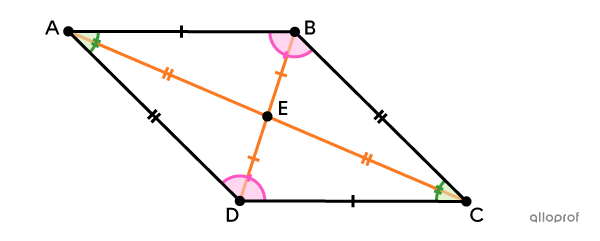
Il a 2 paires de côtés opposés parallèles.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Propriétés
Il a 2 paires d’angles opposés isométriques.||\begin{align}\angle{ABC}&\cong\angle{ADC}\\ \angle{DAB}&\cong\angle{BCD}\end{align}||
Les angles consécutifs sont supplémentaires.||\begin{align}\text{m}\angle{BAD}+\text{m}\angle{ADC}&=180^\circ\\\text{m}\angle{BAD}+\text{m}\angle{ABC}&=180^\circ\\ \text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\\\text{m}\angle{ADC}+\text{m}\angle{BCD}&=180^\circ\end{align}||
Il a 2 paires de côtés opposés isométriques.||\begin{align}\overline{AB} &\cong \overline{CD}\\\overline{AD} &\cong \overline{BC}\end{align}||
Les diagonales se coupent en leur milieu.||\begin{align}\overline{BE}&\cong \overline{DE}\\ \overline{AE}&\cong \overline{CE}\end{align}||
Le losange
Un losange est un quadrilatère convexe dont les 4 côtés sont isométriques.
Le losange possède plusieurs propriétés :
-
il a des angles opposés isométriques;
-
il a des angles consécutifs supplémentaires;
-
ses côtés opposés sont parallèles;
-
ses diagonales se coupent en leur milieu et sont perpendiculaires.
Définition
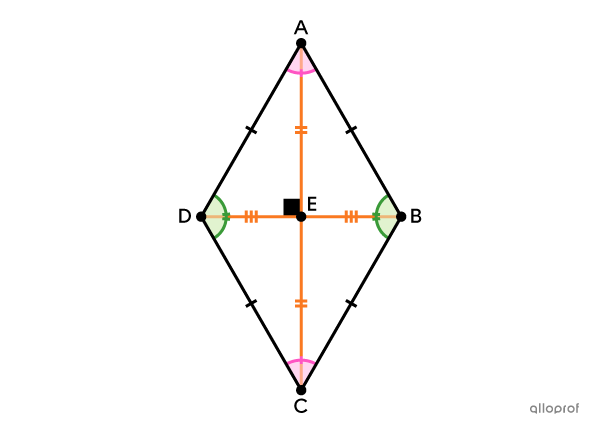
Les 4 côtés sont isométriques.||\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{AD}||
Propriétés
Il a 2 paires d’angles opposés isométriques.||\begin{align}\angle{ABC}&\cong\angle{ADC}\\ \angle{DAB}&\cong\angle{DCB}\end{align}||
Les angles consécutifs sont supplémentaires. ||\begin{align}\text{m}\angle{DAB}+\text{m}\angle{ABC}&=180^\circ\\
\text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\\
\text{m}\angle{BCD}+\text{m}\angle{CDA}&=180^\circ\\
\text{m}\angle{CDA}+\text{m}\angle{DAB}&=180^\circ\end{align}||
Il a 2 paires de côtés opposés parallèles.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel\overline{BC}\end{align}||
Les diagonales se coupent en leur milieu.||\begin{align}\overline{DE}&\cong \overline{BE}\\ \overline{AE}&\cong \overline{CE}\end{align}||
Les diagonales sont perpendiculaires.||\overline{AC}\perp\overline{BD}||
Le rectangle
Un rectangle est un quadrilatère convexe ayant 4 angles droits.
Le rectangle possède plusieurs propriétés :
-
ses côtés opposés sont parallèles et isométriques;
-
ses diagonales sont isométriques et se coupent en leur milieu.
Définition
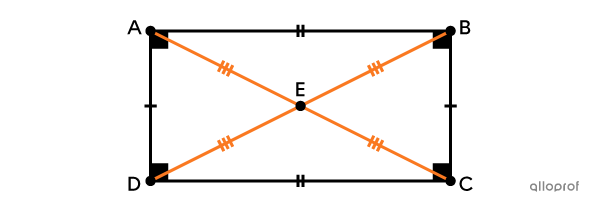
Les 4 angles sont de |90^\circ.|||\text{m}\angle{ABC}=\text{m}\angle{BCD}=\text{m}\angle{CDA}=\text{m}\angle{DAB}=90^\circ||
Propriétés
Il a 2 paires de côtés opposés parallèles.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Il a 2 paires de côtés opposés isométriques.||\begin{align}\overline{AB} &\cong \overline{CD}\\\overline{AD} &\cong \overline{BC}\end{align}||
Les diagonales sont isométriques.||\overline{AC}\cong\overline{DB}||
Les diagonales se coupent en leur milieu.||\begin{align}\overline{AE}&\cong \overline{CE}\\ \overline{DE}&\cong \overline{BE}\end{align}||
Le carré
Le carré est un quadrilatère ayant 4 angles droits et 4 côtés isométriques.
Le carré possède plusieurs propriétés :
-
ses côtés opposés sont parallèles;
-
ses diagonales sont perpendiculaires, se coupent en leur milieu et sont isométriques.
Définition
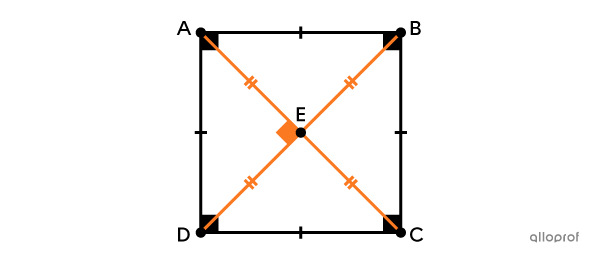
Les 4 angles sont de |90^\circ.|||\text{m}\angle{ABC}=\text{m}\angle{BCD}=\text{m}\angle{CDA}=\text{m}\angle{DAB}=90^\circ||
Les 4 côtés sont isométriques.||\overline{AB} \cong \overline{BC}\cong \overline{CD} \cong \overline{AD}||
Propriétés
Il a 2 paires de côtés parallèles.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Les diagonales sont perpendiculaires.||\overline{AC}\perp\overline{BD}||
Les diagonales se coupent en leur milieu.||\begin{align}\overline{AE}&\cong \overline{CE}\\ \overline{BE}&\cong \overline{DE}\end{align}||
Les diagonales sont isométriques.||\overline{AC}\cong\overline{BD}||
Exercice
Jeu
