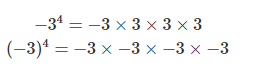Populaires

Salut Sami!

Pour résoudre une équation, tu dois toujours placer les termes semblables d'un côté de l'équation, et les constantes de l'autre côté. Prenons un exemple pour mieux comprendre.

On a l'équation :

$$ \frac{3x}{4} - \frac{6}{7} = \frac{2x}{3} + \frac{3}{14} $$

Les termes semblables sont les termes ayant les mêmes variables (les mêmes inconnus). et ces variables sont affectées des mêmes exposants. Donc, nos termes semblables sont ici \(\frac{3x}{4} \) et \( \frac{2x}{3}\), puisqu'ils contiennent tous les deux la variable x affectée d'un exposant 1.

Les constantes sont les termes qui ne contiennent pas de variables, soit ici \(- \frac{6}{7}\) et \(\frac{3}{14} \).

Notre but sera d'abord de placer d'un côté de l'égalité les deux termes semblables, et de l'autre côté les constantes. Pour ce faire, nous allons commencer par déplacer un des deux termes semblables de l'autre côté (peu importe lequel), et ce, en effectuant l'opération inverse.

Déplaçons \( \frac{2x}{3}\) du côté gauche de l'égalité. Puisque l'opération inverse d'une addition est une soustraction, nous allons devoir soustraire \( \frac{2x}{3}\) de chaque côté de l'équation, comme ceci :

$$ \frac{3x}{4} - \frac{6}{7} = \frac{2x}{3} + \frac{3}{14} $$

$$ \frac{3x}{4} - \frac{6}{7} - \frac{2x}{3} = \frac{2x}{3} + \frac{3}{14} - \frac{2x}{3} $$

En le soustrayant de chaque côté, cela nous permet de l'éliminer du côté droit de l'équation :

$$ \frac{3x}{4} - \frac{6}{7} - \frac{2x}{3} = \frac{3}{14} $$

On a ainsi déplacé le terme \( \frac{2x}{3}\) afin qu'il soit du même côté que son terme semblable.

Passons maintenant aux constantes. Nous allons déplacer la constante \(\frac{6}{7}\) de l'autre côté. Puisque l'opération inverse d'une soustraction est une addition, nous allons donc additionner \(\frac{6}{7}\) de chaque côté :

$$ \frac{3x}{4} - \frac{6}{7} - \frac{2x}{3} + \frac{6}{7}= \frac{3}{14}+\frac{6}{7} $$

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{3}{14}+\frac{6}{7} $$

On a ainsi réussi à placer nos termes semblables d'un côté et nos constantes de l'autre! La prochaine étape sera d'additionner les constantes, et d'additionner les coefficients des termes semblables. Pour cela, il faudra placer les fractions sur un même dénominateur.

Commençons par les constantes. On a les dénominateurs 14 et 7, il faut donc trouver le PPCM de 14 et 7, qui est 14. On peut alors transformer la fraction \(\frac{6}{7} \) en une fraction équivalente donc le dénominateur sera 14.

$$ \frac{6}{7} = \frac{?}{14} $$

Puisqu'on doit multiplier le dénominateur 7 par 2 pour obtenir 14, il faut alors aussi multiplier le numérateur 6 par 2 :

$$ \frac{6}{7} = \frac{6\times2}{7\times 2}=\frac{12}{14} $$

On remplace alors \(\frac{6}{7} \) par sa fraction équivalente dans l'équation :

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{3}{14}+\frac{12}{14} $$

Maintenant que les deux fractions sont sur le même dénominateur, on peut additionner leur numérateur :

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{3+12}{14} $$

$$ \frac{3x}{4}- \frac{2x}{3}= \frac{15}{14} $$

On suit le même principe pour les termes semblables. Il faut placer les fractions \(\frac{3}{4}\) et \(\frac{2}{3}\) sur un même dénominateur. Pour cela, on cherche le PPCM de 4 et 3, soit 12. Il faut alors transformer les deux fractions en des fractions équivalentes dont le dénominateur est 12 :

$$ \frac{3}{4}x- \frac{2}{3}x= \frac{15}{14} $$

$$ \frac{3\times3}{4\times3}x- \frac{2\times4}{3\times4}x= \frac{15}{14} $$

$$ \frac{9}{12}x- \frac{8}{12}x= \frac{15}{14} $$

On peut maintenant soustraire les numérateurs des deux fractions :

$$ \frac{9-8}{12}x= \frac{15}{14} $$

$$ \frac{1}{12}x= \frac{15}{14} $$

Finalement, la dernière étape sera d'éliminer le coefficient de la variable x, soit \(\frac{1}{12}\), et ce, en effectuant l'opération inverse d'une multiplication, soit une division :

$$ \frac{1}{12}x \div \frac{1}{12}= \frac{15}{14} \div \frac{1}{12} $$

$$x= \frac{15}{14} \div \frac{1}{12} $$

Lorsqu'on divise par une fraction, c'est l'équivalent de multiplier par l'inverse de cette fraction :

$$x= \frac{15}{14} \times \frac{12}{1} $$

On peut maintenant multiplier les numérateurs et les dénominateurs ensemble :

$$x= \frac{15\times 12}{14\times 1} $$

$$x= \frac{180}{14} $$

Voilà! Cependant, la réponse n'est pas une fraction irréductible, il faut donc la simplifier. Pour ce faire, on doit diviser le numérateur et le dénominateur par le PGCD de 180 et 14, soit 2 :

$$x= \frac{180\div 2}{14\div 2} $$

$$x= \frac{90}{7} $$

Tu peux laisser ta réponse finale sous forme de fraction impropre comme celle-ci (le numérateur est supérieur au dénominateur), ou tu peux la transformer en un nombre fractionnaire ou un nombre décimal, il faudra alors vérifier ce que l'exercice ou ton professeur te demandera de faire.

Voici des fiches sur ces notions qui pourraient t'être utiles :

• La résolution d'équations et d'inéquations | Secondaire | Alloprof
• Algèbre - Expressions algébriques | Alloprof
• L'addition de fractions | Secondaire | Alloprof
• La soustraction de fractions | Secondaire | Alloprof
• De la fraction au nombre fractionnaire et l'inverse | Secondaire | Alloprof
• Les types de fractions | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! :)