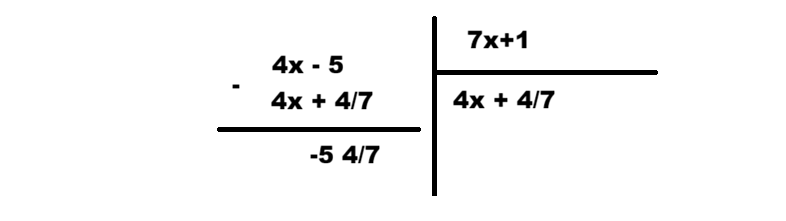Populaires
Re : Question
Bonjour FraiseKappa3158! :D
Merci pour ta question! :)
Pour le forfait 1, il faut effectivement distinguer deux situations :
Situation 1 : lorsque tu es à 300 transactions ou moins.
Dans ce cas, tu paies simplement 50 $, peu importe le nombre de transactions.
Donc, l’équation est :
y=50
Situation 2 : lorsque tu dépasses 300 transactions.
À partir de là, chaque transaction supplémentaire coûte 0,05 $.
On va donc compter seulement les transactions au-delà de 300, d’où le (x−300)
Dans ce cas, l’équation devient :
y=50+0,05(x−300)
Ça permet de rajouter le bon montant uniquement à partir du 301e transaction! :)
Voilà! :) J'espère ça a pu t'aider un peu! :) Je te souhaite une belle journée! :) Si tu as d'autres questions, n'hésite pas à revenir nous voir! :)
Re : Question
Salut FraiseKappa,
Je te remercie d'avoir pensé à nous aujourd'hui et j'espère que tu vas bien.
Ici, la règle serait un mélange de y=50 et y=0,05x+50, comme tu te le demandais. À mon avis, il s'agirait ici en fait d'une fonction qu'on appellerait "définie par partie", comme on les voit ici : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-fonction-definie-par-parties-m1139 .
Grosso modo, elle aura une règle qui va changer à partir d'une certaine valeur de X. En effet, pour X entre 0 et 300, c'est simplement y=50.
Ensuite, pour X plus grand ou égal à 301, ce serait alors la règle y = 0,05(x-300)+50 qui serait de mise. Il faut noter le fait qu'ici on va mettre "x-300" dans la parenthèse après le 0,05; car on ne paie que pour les transactions qui dépassent la 300ème transaction. Sans le "-300", on paierait donc trop cher, car on comptabiliserait aussi les transactions avant la 301ème ;) .
On ne pouvait pas avoir la règle "y = 0,05(x-300)+50" avant en X, car pour x<300, on aurait alors y<50, ce qui ne serait pas logique avec le problème.
N'hésite pas à nous réécrire si jamais on peut faire quoi que ce soit de plus pour toi et j'espère que cela te sera utile. Bonne journée :) !
Re : Question
Bonjour LuneAlpha4604! 🙂
Merci pour ta question! :D
C’est tout à fait normal que la matière devienne plus exigeante au secondaire, ça fait partie du parcours! 😊
Pour t’aider, une bonne stratégie est de te structurer un peu chaque jour. Faire un petit peu d’étude régulièrement, ça fait une grande différence!
Tu peux aussi varier tes méthodes d’apprentissage : changer de technique rend l’étude plus motivante et efficace. N’hésite pas à explorer nos fiches, nos vidéos, nos jeux et nos exercices interactifs : ils sont là pour rendre la compréhension plus simple et plus amusante! 😉
Tu peux également venir nous voir n'importe quand si tu as des questions! ;)
On possède pleins d'autres trucs ici: https://www.alloprof.qc.ca/fr/eleves/bv/exams-et-trucs/trucs-pour-etudier-t2000
Bonne étude et au plaisir de t’aider à nouveau! :D
Re : Question
Salut à toi supernova de l'apprentissage! 😁
Ça nous fait plaisir que tu utilises Alloprof!
Tu peux essayer la minuterie motivante. C'est un outil qui aide à allouer du temps à des travaux afin de rester concentré.e.
Je te laisse aussi ici quelques astuces afin d'améliorer ta concentration lors de ton étude.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re : Question
Bonjour YakPratique397,
Merci pour ta question!
En 1840, même si le Canada-Uni a un parlement élu, celui-ci n'a pas de réelle autorité étant donné que toutes leurs lois doivent être approuvées par le roi (dans ce cas-ci, son représentant, le gouverneur général).
Les deux représentants des provinces du Canada-Ouest et du Canada-Est, Robert Baldwin et Louis-Hippolyte Lafontaine, décident alors de s'allier pour former une majorité au parlement et revendiquer le gouvernement responsable, soit la capacité du gouvernement à voter ses propres lois sans l'approbation du gouverneur général.
C'est un événement historique étant donné que les deux provinces n'avaient jamais réussi à s'entendre, l'une étant de majorité anglophone (le Canada-Ouest) et l'autre, francophone (le Canada-Est).
Baldwin et Lafontaine réussissent donc à obtenir le gouvernement responsable en 1841, leur permettant ainsi de gagner en autonomie par rapport à l'Angleterre.
Tu peux consulter cette fiche pour plus d'informations:
J'espère que ça t'aide! N'hésite pas à nous réécrire si tu as d'autres questions!
Re : Question
Bonjour,
Tu peux utiliser les fractions !
7 entre 4/7 fois dans 4 !
Donc,
Il te restera comme reste - 5 et 4/7.
Si tu as d'autres questions, n'hésite pas à venir les poser !
Bonne journée :)
Re : Question
Salut LoupAlpha923 😁
Il y a plusieurs trucs pour étudier en s'amusant, les voici:
- 📝Réviser avec des jeux t'aidant à apprendre la matière pour ton examen.
- 📌Faire une ''présentation'' devant ta famille, tu leurs explique la matière comme si tu était leur prof.
- 🔎Faire des exercices, et avec la note que tu as voir si tu es prêt/e.
- ✏️Poser des questions sur la matière de l'examen avec tes amis.
J’espère qu'une des techniques t'aideras!😉
HippocampeComique1176
Re : Question
Bonjour PoissonArtistique2749,
Merci d'utiliser la zone d'entraide,
Les calculs de concentration servent à savoir combien de substance il y a dans un certain volume. Pour ne pas se mélanger, il faut toujours utiliser la même formule : concentration = quantité en grammes (masse) ÷ volume. Avant de calculer, on vérifie que les unités sont correctes, surtout que le volume est bien en litres. Écrire la formule avant de mettre les nombres aide beaucoup à éviter les erreurs.
Exemple :
On dissout 8 g de sel dans 2 L d’eau.
Concentration = quantité ÷ volume
8 g ÷ 2 L = 4 g/L
La concentration de la solution est donc de 4 g/L.
Ne lâche pas, Bonne étude, Bon travail, bon succès, n'hésite pas à revenir nous voir si tu as d'autres questions, etc.
LefraniResponsable4446
Question
Allo quelqu'un peux me donne des trucs pour les calculs de concentration je mélange tout ensemble 😓
Re : Question
Re-salut !
Parfait ! Résolvons-le ensemble :
$$ (\frac{1}{2})^{\frac{20}{t_{1/2}}} = 0.25$$
Pour ce faire, tu dois te servir des lois des logarithmes. On utilise les logarithmes parce que l’inconnue (t_1/2) se trouve dans un exposant.
Les logarithmes sont justement l’outil qui permet de faire descendre un exposant pour pouvoir le manipuler.
Rappel : log(a^b) = b · log(a)
Ainsi,
$$ (\frac{1}{2})^{\frac{20}{t_{1/2}}} = 0.25$$
$$ \log{(\frac{1}{2})^{\frac{20}{t_{1/2}}}} = \log{0.25} $$
$$ \frac{20}{t_{1/2}}} * \log{(\frac{1}{2}) = \log{0.25} $$
Je te laisse poursuivre la résolution.
Voici un lien utile :
N'hésite pas à revenir nous voir si tu bloques toujours !
Bonne journée :)