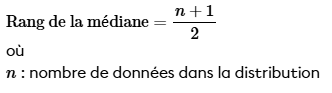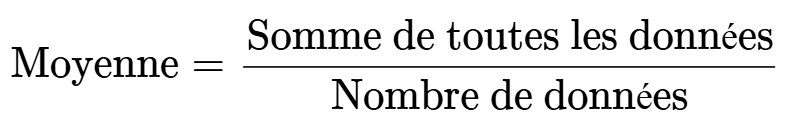Populaires

Bonjour,

Je ne sais pas pas où mettre mon premier point dans un problème de partie entière et si il doit être fermé ou ouvert. Est ce que vous pouvez m'expliquer si possible avec des exemples.

Merci

Une droite est complètement définie par deux points.

Tu connais deux points: (0,15) et (18, 12.3)

Tu peux déjà tracer la droite reliant ces deux points sur le graphique.

La règle est y = ax + b

ici x = le nombre de glaçons et y = la température de l'eau (ºC)

a = la pente de la droite

avec les deux points on détermine la valeur de la pente:

=> a = (12.3 - 15)/(18 - 0) = -0.15

donc y = -0.15x + b

en utilisant un des points, (0,15) par exemple, tu trouves b.

Une fois la règle connue, tu peux compléter le tableau.

Salut!

Pour résoudre une inéquation (ou une équation), tu dois toujours placer les termes semblables d'un côté de l'équation, et les constantes de l'autre côté. Prenons un exemple pour mieux comprendre.

On a l'équation :

$$ 4x - 6 < 2x + 10$$

Les termes semblables sont les termes ayant les mêmes variables (les mêmes inconnus), et ces variables sont affectées des mêmes exposants. Donc, nos termes semblables sont ici \(4x \) et \( 2x\), puisqu'ils contiennent tous les deux la variable x affectée d'un exposant 1.

Les constantes sont les termes qui ne contiennent pas de variables, soit ici \(-6\) et \(10\).

Notre but sera d'abord de placer d'un côté de l'égalité les deux termes semblables, et de l'autre côté les constantes. Pour ce faire, nous allons commencer par déplacer un des deux termes semblables de l'autre côté (peu importe lequel), et ce, en effectuant l'opération inverse.

Déplaçons \(2x\) du côté gauche de l'égalité. Puisque l'opération inverse d'une addition est une soustraction, nous allons devoir soustraire \( 2x\) de chaque côté de l'équation, comme ceci :

$$ 4x - 6 -2x< 2x + 10-2x$$

En le soustrayant de chaque côté, cela nous permet de l'éliminer du côté droit de l'équation :

$$ 4x - 6 -2x< 10$$

On a ainsi déplacé le terme \(2x\) afin qu'il soit du même côté que son terme semblable.

Passons maintenant aux constantes. Nous allons déplacer la constante \(6\) de l'autre côté. Puisque l'opération inverse d'une soustraction est une addition, nous allons donc additionner  \(6\) de chaque côté :

$$ 4x - 6 -2x+6< 10+6$$

$$ 4x -2x< 10+6$$

On a ainsi réussi à placer nos termes semblables d'un côté et nos constantes de l'autre! La prochaine étape sera d'additionner les constantes, et d'additionner les coefficients des termes semblables. Commençons par les constantes. Puisque 10+6 donne 16, nous avons :

$$ 4x -2x< 16$$

Pour soustraire les termes semblables, il faut soustraire leur coefficient, c'est-à-dire le nombre devant la variable x.

$$ (4-2)x< 16$$

$$ 2x< 16$$

Finalement, la dernière étape sera d'éliminer le coefficient de la variable x, soit \(2\), et ce, en effectuant l'opération inverse d'une multiplication, soit une division :

$$ \frac{2x}{2}  < \frac{16}{2} $$

$$x<8$$

Voilà! Attention, si on avait divisé l'équation par un nombre négatif (exemple si on avait divisé par -2 au lieu de 2), alors il aurait fallu inverser le signe d'inégalité (< serait devenu >).

Voici des fiches sur ces notions qui pourraient t'être utiles :

• La résolution d'équations et d'inéquations | Secondaire | Alloprof
• Algèbre - Expressions algébriques | Alloprof

Ensuite, le mode est la valeur qui apparaît le plus souvent dans un ensemble de données. Pour trouver le mode d'une distribution, il n'y a donc aucun calcul à faire, il faut simplement regarder le nombre qui apparait le plus de fois dans la distribution de nombres. Voici un exemple :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La médiane est la valeur du milieu lorsque les nombres sont classés dans l'ordre croissant (ou décroissant). Pour calculer le rang du nombre qui est la médiane, on utilise cette formule :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Par exemple, si tu as les nombres suivants :

2, 3, 6, 7, 7

Pour trouver la médiane, on les classe d'abord dans l'ordre (ils le sont déjà ici). La médiane est le nombre au milieu, donc ici, c'est 6.

2, 3, 6, 7, 7

On a 5 nombres au total. En utilisant la formule, on obtient :

$$ \frac{5+1}{2}=3$$

On trouve donc que la médiane est le 3e nombre de la série, et c'est le nombre 6 qui est au rang 3.

Pour calculer une moyenne, il faut suivre la formule suivante :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici un exemple :

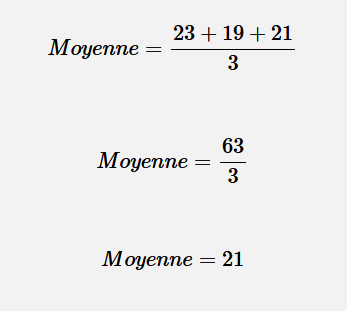
Voici la température des trois derniers jours : 23 degrés, 19 degrés et 21 degrés. Quelle est la moyenne de la température des trois derniers jours ?

Appliquons donc cette formule à ce problème :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Il a donc fait en moyenne 21 degrés.

Je te conseille de te pratiquer en effectuant des exercices sur ces notions. La pratique est la clé pour bien maitriser une notion! En voici quelques-uns qui pourraient t'intéresser :

• Moyenne, médiane, mode et étendue -- Ensembles triés (Ensembles de 15 de 100 à 999) (A)
• Moyenne, médiane, mode et étendue -- Ensembles non triés (Ensembles de 10 de 1 à 10) (A)
• Médiane, étendue et moyenne
• 2nd - Exercices corrigés - Statistiques - Calculs de médianes
• Médiane d'une série statistique

J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! :)