Subjects
Grades
Circles are part of the conics. It is obtained by the intersection of a cone and a plane.
The circle is the geometric locus of all points equidistant from a point called the centre.
Any point |(x,y)| that belongs to a circle can be found using Pythagorean Theorem (also called the Pythagorean Relation).
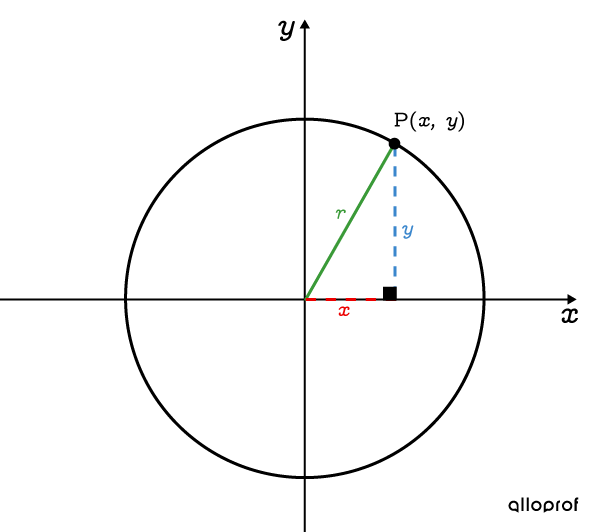
The equation that defines a circle centred at the origin uses parameter |r.|
||x^2+ y^2= r^2||
where
||r=\text{radius of a circle}||
The value of radius |r| must be found to determine the equation of a circle centred at the origin.
Find the value of parameter |\color{#3a9a38}r,| the circle’s radius. If necessary, substitute |x| and |y| with a point on the circle and solve the equation.
Write the equation of the circle.
Find the equation of the circle centred at the origin that passes through point |(7,-3).|
Place the centre of the circle at the origin of the Cartesian plane.
Use the equation to find parameter |\color{#3a9a38}r|.
Starting from the centre, use a compass to sketch a circle whose radius is equal to |\color{#3a9a38}r.|
Sketch the circle of the equation |x^2+y^2=36.|
The Pythagorean Theorem can be used for any point |(x,y)| that belongs to the circle even if it is not centred at the origin.
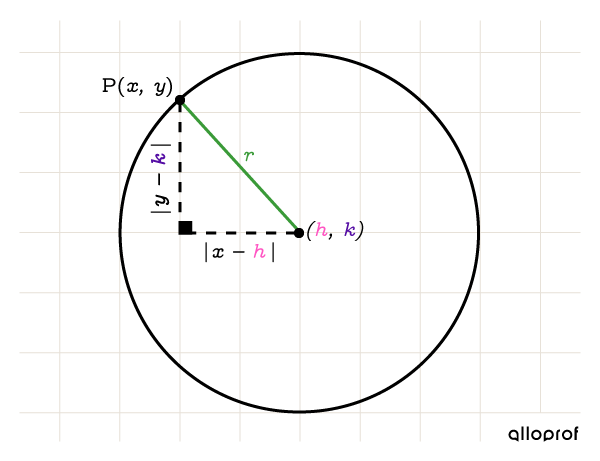
The equation that defines a circle not centred at the origin uses parameters |r,| |h,| and |k.|
||(x-h)^2+(y-k)^2= r^2||
where
||\begin{align} r&=\text{radius of the circle}\\ (h,k)&=\text{coordinates of the circle’s centre}\end{align}||
Find the value of radius |r| and coordinates |(h, k)| of the centre to find the equation of a circle not centred at the origin.
Find the values of parameters |\color{#FF55C3}h| and |\color{#560FA5}k| from the coordinates of the circle’s centre.
Find the value of parameter |\color{#3a9a38}r,| the radius of the circle. If necessary, substitute |x| and |y| with a point on the circle. Then, solve the equation.
Write the equation of the circle.
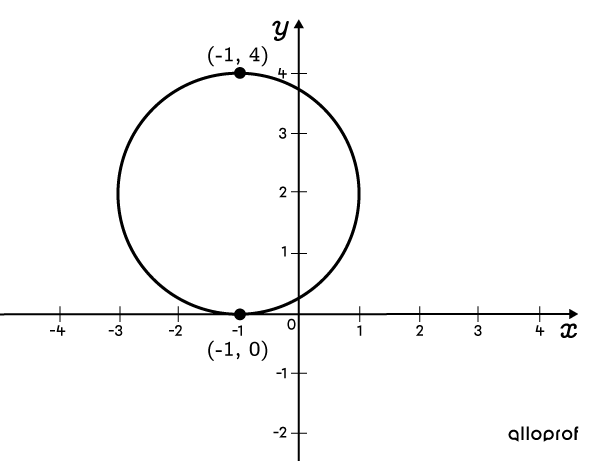
Find the equation of a circle which passes through points |(-1, 0)| and |(-1, 4).|
Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and place the centre of the circle.
Determine parameter |\color{#3a9a38}r| in the equation.
Starting from the centre, use a compass to sketch a circle whose radius is equal to |\color{#3a9a38}r.|
Sketch the circle with the equation: |(x+4)^2+(y-3)^2=16.|
When we want to represent a region bounded by a circle, we apply the following relations.
|
Sector of the Cartesian Plane |
Graphic Representation |
Corresponding Inequality |
|---|---|---|
|
The exterior, excluding the curve |
 |
||\begin{align}x^2&+y^2>r^2\\\\(x-h)^2&+(y-k)^2>r^2\end{align}|| |
|
The interior, excluding the curve |
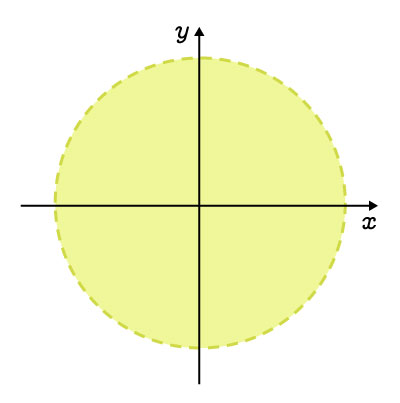 |
||\begin{align}x^2&+y^2<r^2\\\\(x-h)^2&+(y-k)^2<r^2\end{align}|| |
|
The exterior, including the curve |
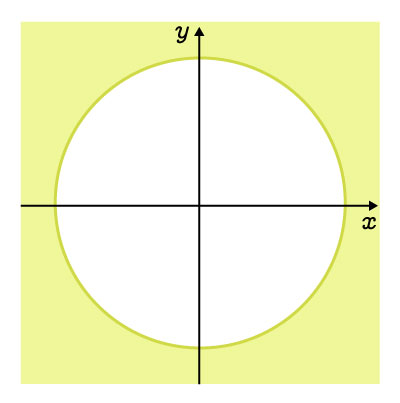 |
||\begin{align}x^2&+y^2\geq r^2\\\\(x-h)^2&+(y-k)^2\geq r^2\end{align}|| |
|
The interior, including the curve |
 |
||\begin{align}x^2&+y^2\leq r^2\\\\(x-h)^2&+(y-k)^2\leq r^2\end{align}|| |
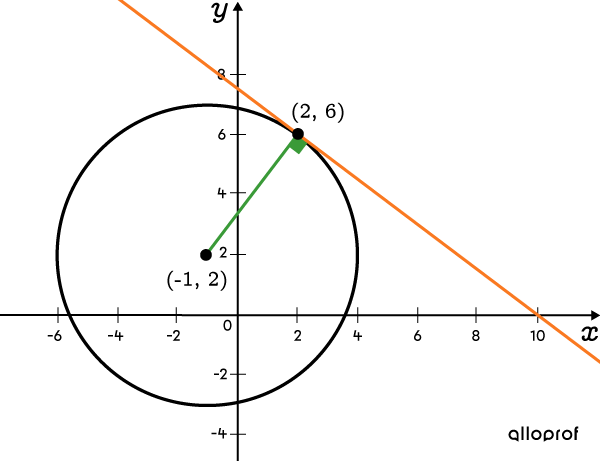
A tangent to a circle is a line perpendicular to the radius that passes through the point of tangency.
Find the slope of the line that passes through the centre of the circle and the point of tangency.
Find the slope of the tangent line using the relationship between two perpendicular lines.
Find the y-intercept of the tangent line using its slope and the coordinates of the point of tangency.
Write the tangent line’s equation.
Find the equation of the line tangent to the circle with the following equation: |(x+1)^2+(y-2)^2=25| at the point |(2,6).|
The general form of the equation of all conics, including the circle, for which the horizontal axis is parallel to the x-axis and the vertical axis is parallel to the y-axis is: || Ax^2+ By^2+Cx+Dy+E=0.||