Subjects
Grades
Parabola (Conic)
Concept sheet | Mathematics
Secondary
5
Table of contents
- Top of page
- Properties of Parabolas
- Parabola Centred at the Origin
- Equation of a Parabola Centred at the Origin
- Properties of Parabolas Centred at the Origin
- Graphing a parabola centred at the origin using its equation
- Parabola Not Centred at the Origin
- Equation of a Parabola Not Centred at the Origin
- Properties of Parabolas Not Centred at the Origin
- Determine the equation of a parabola not centred at the origin
- Graphing a Parabola Not Centred at the Origin Using Its Equation
- Inequality of a Parabola
- See also
The parabola is one of the conics. It is obtained by the intersection of a conical surface and a plane.
A parabola is the geometric locus of all points located at equal distance from a fixed line, called the directrix, and a fixed point, called the focus.
Properties of Parabolas
-
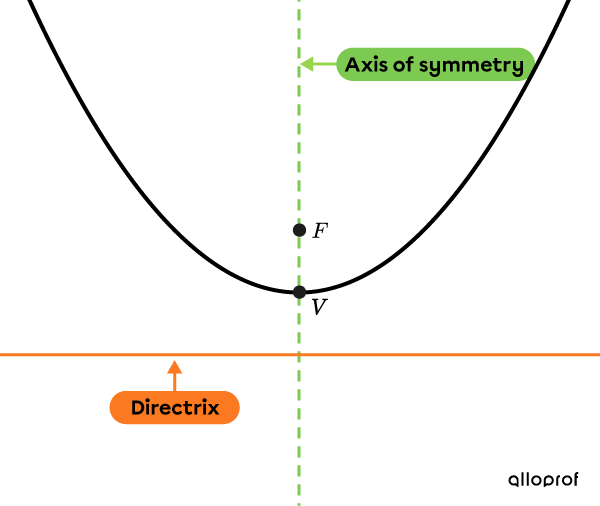
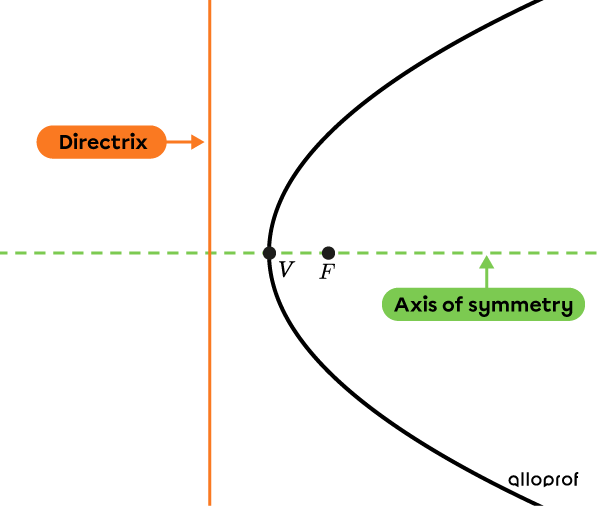
Parabolas have a focus, |F.|
-
Parabolas have a vertex, |V.|
-
Parabolas have a line called the directrix.
-
The line perpendicular to the directrix, passing through the focus and the vertex, is the axis of symmetry.
-
Vertex |V| is equidistant from the focus |F| and the directrix.
Vertical parabola
A parabola is vertical when its axis of symmetry is vertical.
Horizontal parabola
A parabola is horizontal when its axis of symmetry is horizontal.
Parabola Centred at the Origin
Equation of a Parabola Centred at the Origin
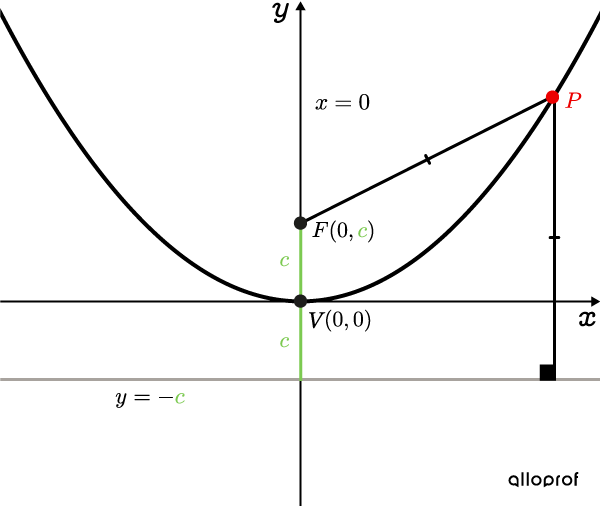
The equation that defines a parabola centred at the origin uses parameter |c.| Depending on its orientation, there are two different equations.
Vertical parabola
||x^2=4cy||Equation of the directrix: ||y=-c||
Horizontal parabola
||y^2=4cx||Equation of the directrix: ||x=-c||
where
|\vert c \vert :| distance between the vertex and the focus or between the vertex and the directrix
In the equation for a vertical parabola |x| is squared, while |y| is squared in the equation for a horizontal parabola equation.
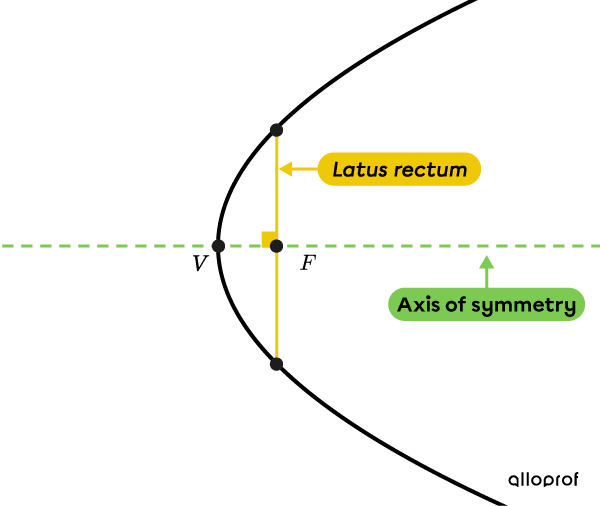
The latus rectum is a line segment that passes through the focus of a parabola and is perpendicular to its axis of symmetry. The length of a parabola’s latus rectum is |4c.| The latus rectum determines the opening of the parabola at the focus.
Properties of Parabolas Centred at the Origin
Here are the graphic representations of the two types of parabolas with the placement of important points and their coordinates.
Vertical parabola
If |c>0,| the parabola opens upwards.
If |c<0,| the parabola opens downwards.
Horizontal parabola
If |c>0,| the parabola opens to the right.
If |c<0,| the parabola opens to the left.
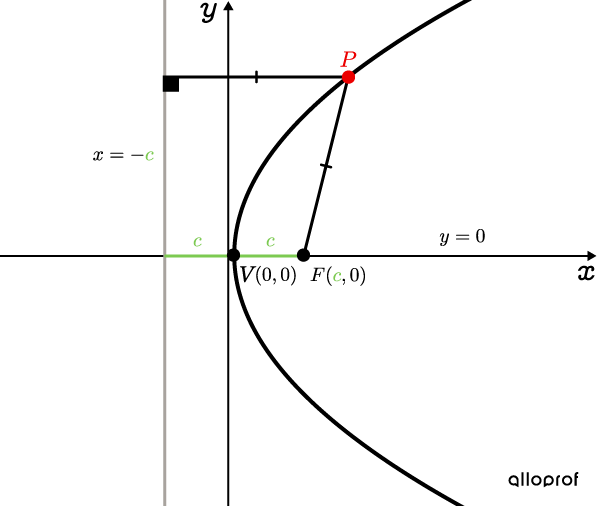
All |\color{#EC0000}P| points are equidistant from the directrix and focus |F.|
Determine the equation of a parabola centred at the origin
To determine the equation of a parabola centred at the origin, first find the value of parameter |c.|
-
Based on the parabola’s orientation, determine the sign of parameter |\color{#3a9a38}c| and the equation to use.
-
Determine the value of parameter |\color{#3a9a38}c| using one of the following strategies:
a) If the equation of the directrix is given, find the value of |\color{#3a9a38}c.|
b) If the coordinates of the focus are provided, find the value of |\color{#3a9a38}c.|
c) If a point on the parabola is given, substitute its coordinates into the parabola’s equation.
-
Write the parabola’s equation.
Here is an example where the equation of the directrix is provided.
Determine the equation of the following parabola.
See solution
Graphing a parabola centred at the origin using its equation
-
Determine the parabola’s orientation.
-
Use parameter |\color{#3a9a38}{c}| to determine the coordinates of the focus and the equation of the directrix.
-
Find other points on the parabola using the equation.
-
Draw the parabola and its directrix.
Sketch the parabola whose equation is |x^2=14y.|
See solution
Here is an animation to help you understand the different relationships and the role of parameters in the parabola.
Parabola Not Centred at the Origin
Equation of a Parabola Not Centred at the Origin
The equation that defines the parabola not centred at the origin uses parameters |c,| |h,| and |k.| As with the parabola centred at the origin, there are two different equations depending on its orientation.
Vertical parabola
||(x-h)^2=4c(y-k)|| Equation of the directrix:||y=k-c||
Horizontal parabola
||(y-k)^2=4c(x-h)|| Equation of the directrix:||x=h-c||
where
|\vert c \vert:| distance between the vertex and the focus or between the vertex and the directrix
|(h,k):| coordinates of the parabola’s vertex
Properties of Parabolas Not Centred at the Origin
Here are graphic representations of the two types of parabolas with the placement of important points and their coordinates.
Vertical parabola
If |c>0,| the parabola opens upwards.
If |c<0,| the parabola opens downwards.
Horizontal parabola
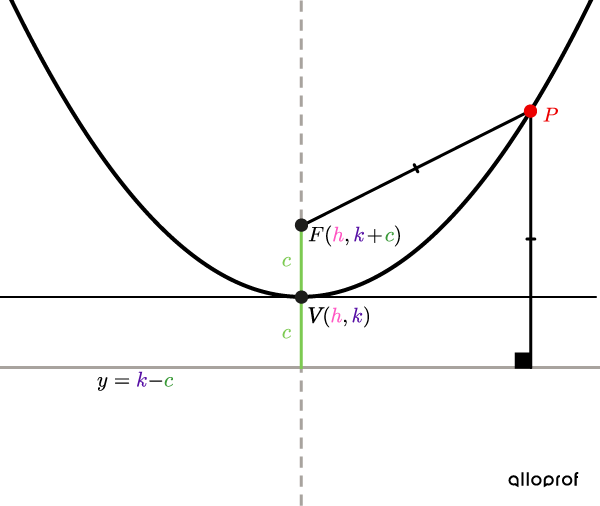
If |c>0,| the parabola opens to the right.
If |c<0,| the parabola opens to the left.
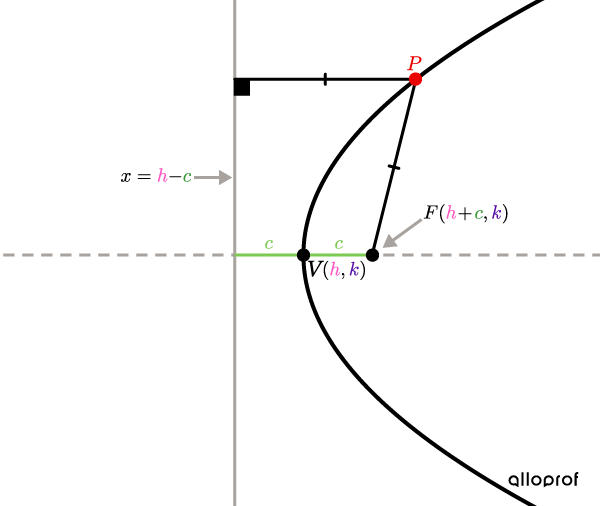
All points |\color{#EC0000}P| are equidistant from the directrix and focus |F.|
Determine the equation of a parabola not centred at the origin
To determine the equation of a parabola not centered at the origin, it is necessary to find the value of parameters |c,| |h,| and |k.|
-
Use the orientation of the parabola to determine the sign of parameter |\color{#3a9a38}c| and the equation.
-
Determine the value of parameters |\color{#3a9a38}c,| |\color{#FF55C3}h,| and |\color{#560FA5}k.| If one or more of these parameters are missing, use one of the following strategies:
a) If the vertex and the equation of the directrix are provided, determine parameter |\color{#3a9a38}c| by substituting the information into the equation of the directrix.
b) If the vertex and a point belonging to the parabola are provided, determine parameter |\color{#3a9a38}c| by substituting the information into the parabola’s equation.
c) If the coordinates of the focus and the equation of the directrix are provided, deduce the missing parameters using the parabola’s properties.
-
Write the parabola’s equation.
Here is an example where the equation of the directrix and the coordinates of the focus are given.
Determine the equation of the following parabola.
See solution
Graphing a Parabola Not Centred at the Origin Using Its Equation
-
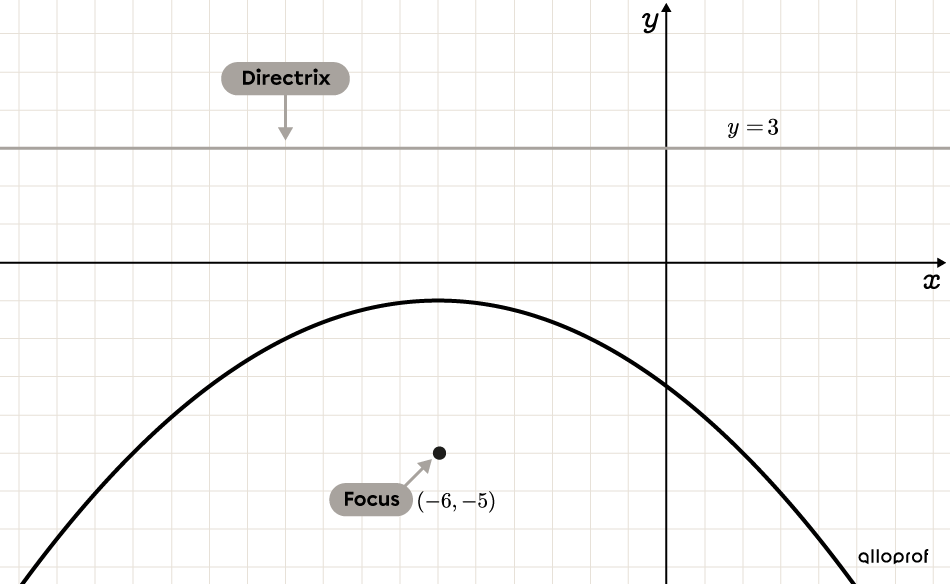
Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and mark the parabola’s vertex.
-
Determine the parabola’s orientation.
-
Determine the coordinates of the focus and the equation of the directrix using parameter |\color{#3a9a38}c.|
-
Use the equation to find other points on the parabola.
-
Sketch the parabola and its directrix.
Draw the parabola whose equation is |(y-1)^2=-8(x+3).|
See solution
Inequality of a Parabola
Apply the following properties when representing a region bounded by a parabola.
A parabola’s interior corresponds to the region where the focus is located. The signs of inequality are less than |(<)| or less than or equal to |(\leq).|
Conversely, the exterior is the region where the focus is not located. The signs are greater than |(>)| or greater than or equal to |(\geq).|
Vertical parabola |
||
|
Region of the Cartesian Plane |
Graphical Representation |
Corresponding Inequality |
|---|---|---|
|
The interior, excluding the curve |
 |
||\begin{align}x^2&<4cy\\\\ |
|
The exterior, excluding the curve |
 |
||\begin{align}x^2&>4cy\\\\ |
Horizontal parabola |
||
|
Region of the Cartesian Plane |
Graphical Representation |
Corresponding Inequality |
|
The interior, excluding the curve |
 |
||\begin{align}y^2&<4cx\\\\ |
|
The exterior, excluding the curve |
 |
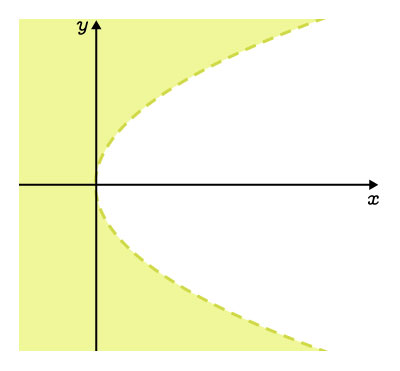||\begin{align}y^2&>4cx\\\\ |
To include the points that are on the parabola, change the inequality symbols |<,>| for symbols |\leq,\geq.|