StudentsParentsTeachersHelp ZoneAllofrançais
Students
ParentsTeachersHelp Zone
My account
Create an account
Home
Ask a question
Subjects
Mathematics
French
Coming Soon
Chemistry
Science and Technology
History
Physics
Geography
English Language Arts
Indigenous content
Coming Soon
Financial Education
Contemporary World
Grades
Grade 1
Grade 2
Grade 3
Grade 4
Grade 5
Grade 6
Secondary 1
Secondary 2
Secondary 3
Secondary 4
Secondary 5
Explore
Concept sheets
Exercises
Games
Videos
Crash Courses
Exam prep and study tips
Mathematics
French
Coming Soon
Chemistry
Science and Technology
History
Physics
Geography
English Language Arts
Indigenous content
Coming Soon
Financial Education
Contemporary World
Grade 1
Grade 2
Grade 3
Grade 4
Grade 5
Grade 6
Secondary 1
Secondary 2
Secondary 3
Secondary 4
Secondary 5
Concept sheets
Exercises
Games
Videos
Crash Courses
Exam prep and study tips
Mathematics
Ellipse (Conic)
Show more

Ellipse (Conic)

Concept sheet | Mathematics
Secondary
5
Table of contents

The ellipse is one of the conics. It is obtained by the intersection of a cone and a plane.

Definition

An ellipse is the geometric locus of all points whose sum of the distances to 2 fixed points, called foci, is constant.

Properties of an Ellipse

  • An ellipse has two axes of symmetry. The longest is called the major axis, and the shortest, the minor axis.

  • An ellipse has two foci, |F_1| and |F_2.|

  • An ellipse has four vertices, |V_1,| |V_2,| |V_3,| and |V_4.|

  • An ellipse can be vertical or horizontal.

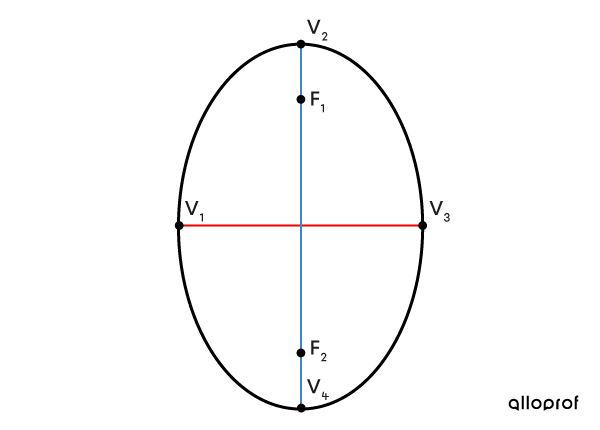
Example of a vertical ellipse with major points identified.

Vertical Ellipse

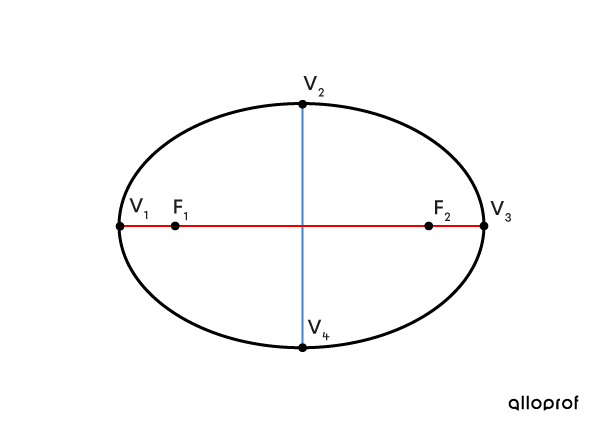
Example of a Horizontal Ellipse with Major Points Identified.

Horizontal Ellipse

Ellipse Centred at the Origin

An ellipse’s equation centred at the origin

The equation that defines an ellipse centred at the origin uses parameters |a| and |b.|

Formula

||\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1|| where ||\begin{align} a &:\text{Half the length of the major axis }\\ b &:  \text{Half the length of the minor axis } \end{align}||

Important!

  • If |\color{#ec0000}a < \color{#3b87cd}b,| the ellipse is vertical.

  • If |\color{#ec0000}a > \color{#3b87cd}b,| the ellipse is horizontal.

Relations in an Ellipse Centred at the Origin

Here are the graphic representations of the two types of ellipses on which the important points are placed. The coordinates of these points in relation to the parameters of the ellipse are also given.

Vertical ellipse

The sum of the distances between a point on a vertical ellipse and its two foci is |2\color{#3b87cd}b.|

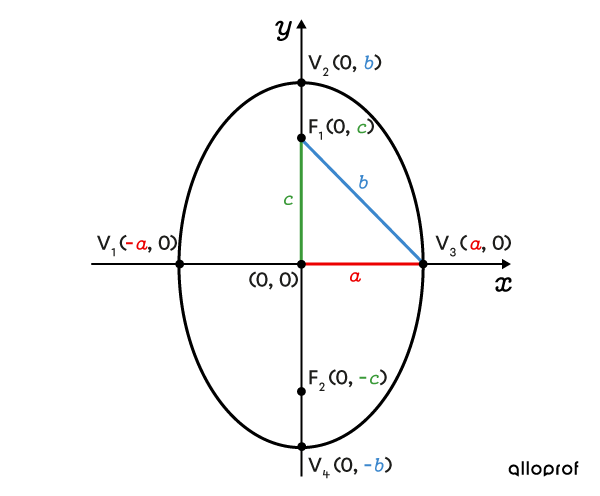
Relations in a vertical ellipse centred at the origin.

The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2||

Horizontal ellipse

The sum of the distances between a point on a horizontal ellipse and its two foci is |2\color{#ec0000}a.|

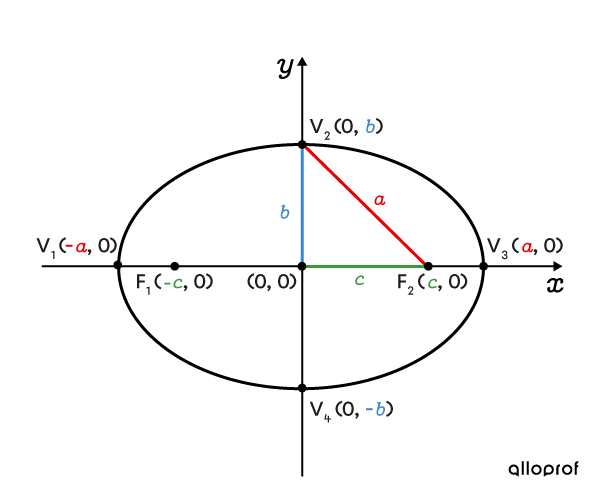
Relations in a horizontal ellipse centred at the origin.

The relationship between parameters |\color{#ec0000}a,|  |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2||

Determine the equation of an ellipse centred at the origin

Find the value of the parameters |a| and |b| to determine the equation of an ellipse centred at the origin.

Rule

Generally, the procedure below is used.

  1. Determine the value of parameter |\color{#ec0000}a,| which corresponds to half of the ellipse’s horizontal axis, and/or that of parameter |\color{#3B87CD}b,| which corresponds to half of the vertical axis.

  2. If one of the two parameters is missing, find it using one of the following strategies:

    a) If parameter |\color{#3A9A38}c| (the distance between the centre and a focus) is given, use the Pythagorean Theorem to determine the value of the missing parameter. ||\begin{align}\text{Vertical ellipse :}&\ \color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2\\ \text{Horizontal ellipse :}&\ \color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2 \end{align}||

    b) If a point on the ellipse |(x,y)| is provided, substitute these coordinates into the equation and determine the value of the missing parameter.

  3. Write the ellipse’s equation.

Example

Determine the equation of this ellipse.

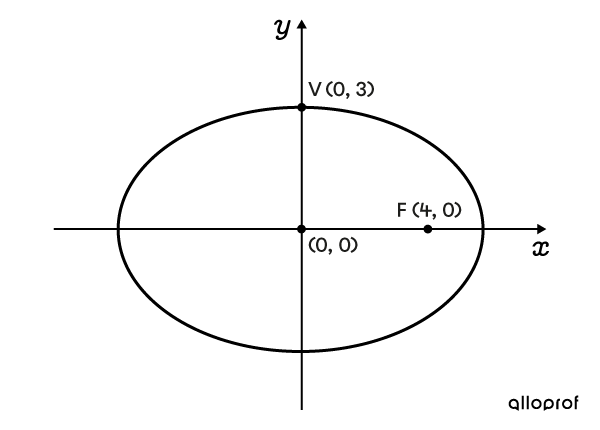
Example of an ellipse with the centre, a vertex, and a focus identified.

See solution

Example

Determine the equation of this ellipse.

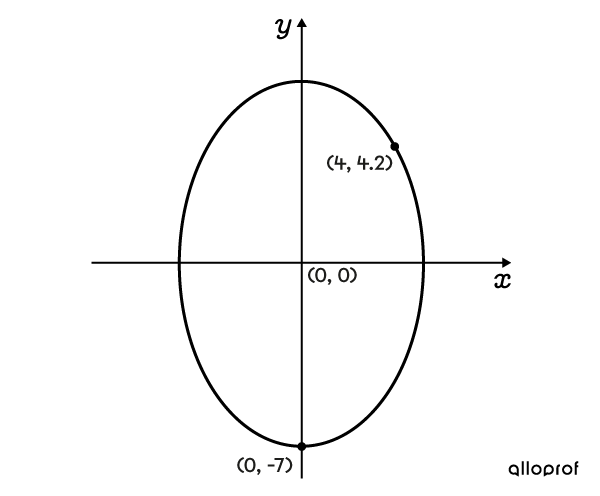
Example of an ellipse with an identified vertex and point.

See solution

Sketch an ellipse centred at the origin using its equation

Follow these steps to draw an ellipse centred at the origin using its equation.

Rule

  1. Mark the centre of the ellipse.

  2. Use the value of parameter |\color{#EC0000}a| to mark the two vertices located on the horizontal axis. Here are the coordinates of the vertices: ||\begin{align}V_1&=(\color{#EC0000}{-a},0)\\ V_3&=(\color{#EC0000}a,0)\end{align}||

  3. Use the value of parameter |\color{#3B87CD}b| to mark the two vertices located on the vertical axis. Here are the vertices’ coordinates: ||\begin{align}V_2&=(0,\color{#3B87CD}b)\\ V_4&=(0,\color{#3B87CD}{-b})\end{align}||

  4. Connect the four vertices to draw the ellipse.

Example

Draw the ellipse represented by the following equation. ||\dfrac{x^{2}}{289}+\dfrac{y^{2}}{196}=1||

See solution

Ellipse Not Centred at the Origin

The equation of an ellipse not centred at the origin

The equation that defines an uncentered ellipse uses parameters |a,| |b,| |h,| and |k.|

Formula

||\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|| or ||\begin{align} a &:\text{Half the length of the horizontal axis }\\ b &: \text{Half the length of the vertical axis }\\ (h,k) &: \text{Coordinates of the ellipse’s centre }\end{align}||

Important!

  • If |\color{#ec0000}a < \color{#3b87cd}b,| the ellipse is vertical.

  • If |\color{#ec0000}a > \color{#3b87cd}b,| the ellipse is horizontal.

Relations in an ellipse not centred at the origin

Vertical ellipse

The sum of the distances between a point on a vertical ellipse and its two foci is |2\color{#3b87cd}b.|

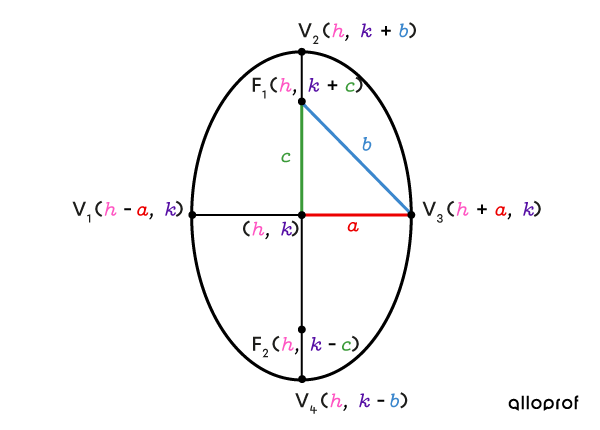
Relations in the vertical ellipse not centred at the origin.

The relationship between the parameters  |\color{#ec0000}a,| |\color{#3b87cd}b| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2||

Horizontal ellipse

The sum of the distances between a point on a horizontal ellipse and its two foci is |2\color{#ec0000}a.|

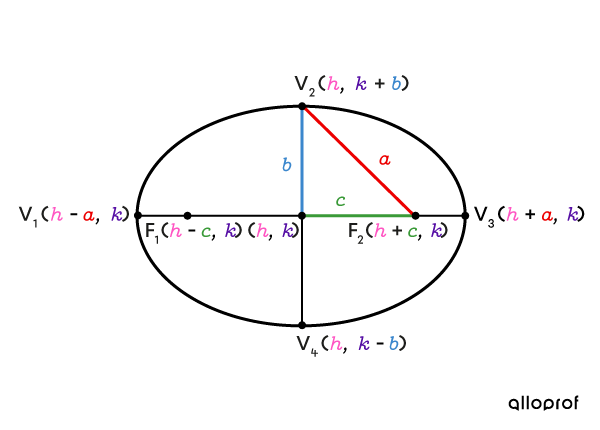
Relations in a horizontal ellipse not centred at the origin.

The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem.
||\color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2||

Determine the equation of an ellipse not centred at the origin

To use a graph to determine the equation of an ellipse not centred at the origin, find the value of parameters |a,| |b,| |h,| and |k.|

Rule

Generally, the process looks like this.

  1. Determine the values of parameters |\color{#FF55C3}h| and |\color{#560FA5}k| from the coordinates of the ellipse’s centre.

  2. Determine the value of parameter |\color{#ec0000}a,| which corresponds to half of the ellipse’s horizontal axis, and/or that of parameter |\color{#3B87CD}b,| which corresponds to half of the vertical axis.

  3. If either parameter |a| or |b| is missing find it using one of the following strategies:

    a) If parameter |\color{#3A9A38}c| (the distance between the centre and a focus) is provided, use the Pythagorean Theorem to determine the missing parameter’s value. ||\begin{align}\text{Vertical ellipse :}&\ \color{#3a9a38}c^2=\color{#3b87cd}b^2-\color{#ec0000}a^2\\ \text{Horizontal ellipse :}&\ \color{#3a9a38}c^2=\color{#ec0000}a^2-\color{#3b87cd}b^2 \end{align}||

    b) If a point on ellipse |(x,y)| is provided, substitute its coordinates into the equation and determine the value of the missing parameter.

  4. Write the ellipse’s equation.

Example

Determine the equation of this ellipse.

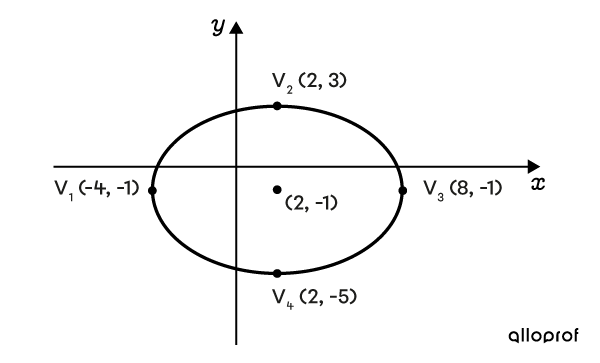
Example of an ellipse not centred at the origin with the centre and its four vertices identified.

See solution

Example

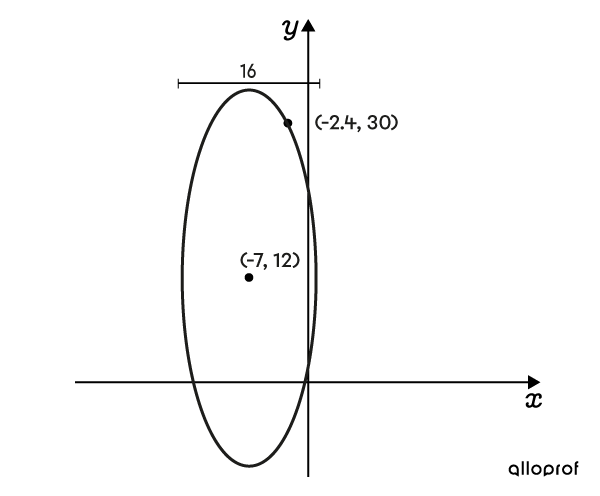
Determine the equation of this ellipse, knowing that its horizontal axis measures |16| units.

Example of an ellipse not centred at the origin with the centre with one point identified.

See solution

Sketch an ellipse not centred at the origin using its equation

Follow these steps to draw an ellipse using its equation.

Rule

  1. Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and mark the ellipse’s centre.

  2. Use the value of parameter |\color{#EC0000}a| to mark the two vertices located on the horizontal axis. Here are the vertices’ coordinates. ||\begin{align}V_1:(\color{#FF55C3}h\color{#EC0000}{-a},\color{#560FA5}k)\\ V_3:(\color{#FF55C3}h\color{#EC0000}{+a},\color{#560FA5}k)\end{align}||

  3. Use the value of parameter |\color{#3B87CD}b| to place the two vertices on the vertical axis. Here are the vertices’ coordinates. ||\begin{align}V_2:(\color{#FF55C3}h,\color{#560FA5}k\color{#3B87CD}{+b})\\ V_4:(\color{#FF55C3}h,\color{#560FA5}k\color{#3B87CD}{-b})\end{align}||

  4. Connect the four vertices to draw the ellipse.

Example

Draw the ellipse represented by the following equation. ||\dfrac{(x-5)^{2}}{64}+\frac{(y+4)^{2}}{100}=1||

See solution

Inequality of an Ellipse

Apply the following relations to represent a region bounded by an ellipse

Sector of the Cartesian Plane

Graphical Representation

Corresponding Inequality

The exterior, excluding the curve
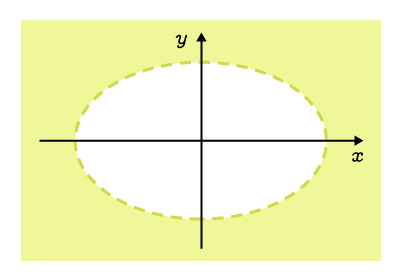Secteur du plan extérieur à l’ellipse, excluant la courbe

||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}>1\\\\
\dfrac{(x-h)^2}{a^2}&+\dfrac{(y-k)^2}{b^2}>1\end{align}||

The interior, excluding the curve
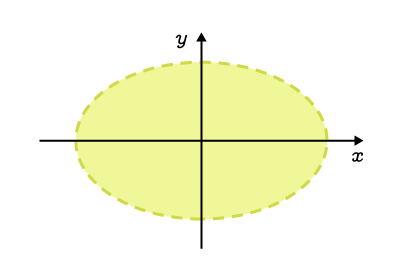Secteur du plan intérieur à l’ellipse, excluant la courbe

||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}<1\\\\
\dfrac{(x-h)^2}{a^2}&+\dfrac{(y-k)^2}{b^2}<1\end{align}||

The exterior, including the curve
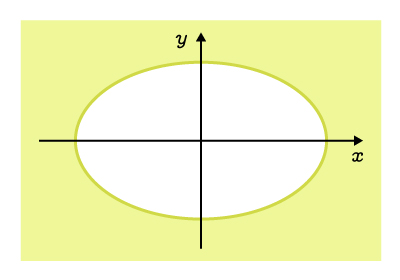Secteur du plan extérieur à l’ellipse, incluant la courbe

||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}\geq1\\\\
\dfrac{(x-h)^2}{a^2}&+\dfrac{(y-k)^2}{b^2}\geq1\end{align}||

The interior, including the curve
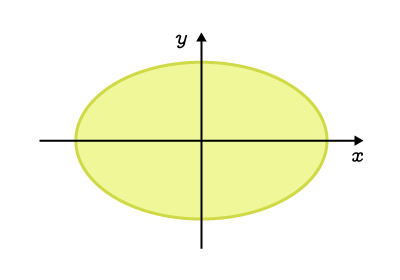Secteur du plan intérieur à l’ellipse, incluant la courbe

||\begin{align}\dfrac{x^2}{a^2}&+\dfrac{y^2}{b^2}\leq1\\\\
\dfrac{(x-h)^2}{a^2}&+\dfrac{(y-k)^2}{b^2}\leq1\end{align}||

Equation of an Ellipse in General Form

The general form of the equation of all conics, including the ellipse, for which the horizontal axis is parallel to the x-axis and the vertical axis is parallel to the y-axis is: || Ax^2+ By^2+Cx+Dy+E=0||

It can be helpful to switch from general form to standard form when solving some problems concerning the ellipse.

Find the standard form of an ellipse’s equation from its equation in general form

See also