Finding Missing Measurements in Plane Figures Using a 2nd Degree Equation

Concept sheet | Mathematics

Secondary

4-5

Top of page
Word Problem
See also

We often have to find missing measurements in plane figures. Sometimes, solving such problems creates a 2^nd degree (quadratic) equation or a system of equations.
To solve them, we must use the quadratic formula or factoring. You also need to know the area and perimeter formulas. Here are the steps to follow to do so.

Rule

Construct an equation or a system of equations from the context.
Solve the equation or the system of equations.
Answer the question.

Here are a series of examples. The first ones are geometry problems that do not have a specific context, while the last one is a word problem that presents a short scenario.

Example

Find the measure of each side of the following isosceles triangle if its perimeter is |100\ \text{cm}.|

See solution

Example

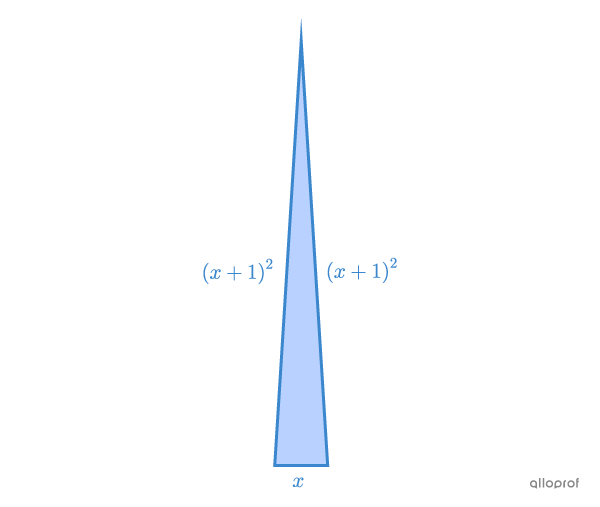
Find the measure of the rectangle’s sides if its area is |15\ \text{m}^2.|

See solution

Example

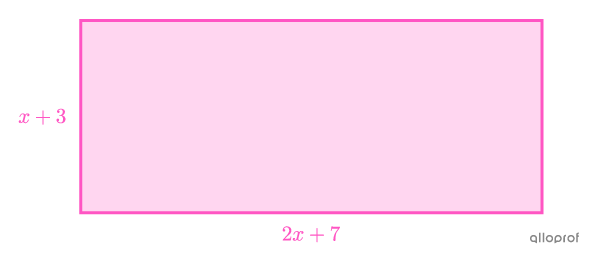
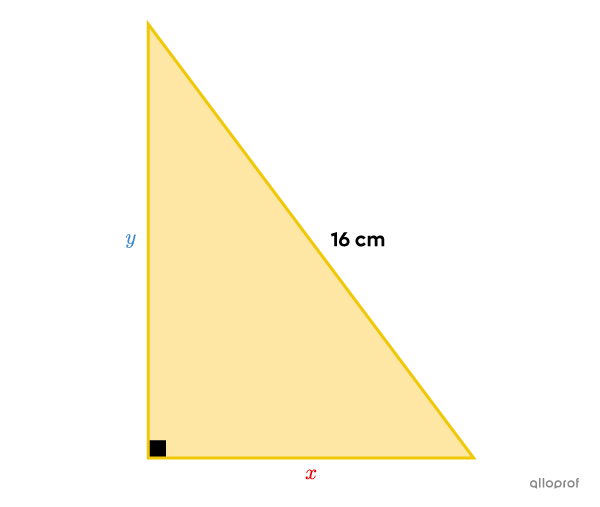
What are the measures of the legs of the triangle if its perimeter is |38.4\ \text{cm}| and its area is |61.44\ \text{cm}^2?|

See solution

Example

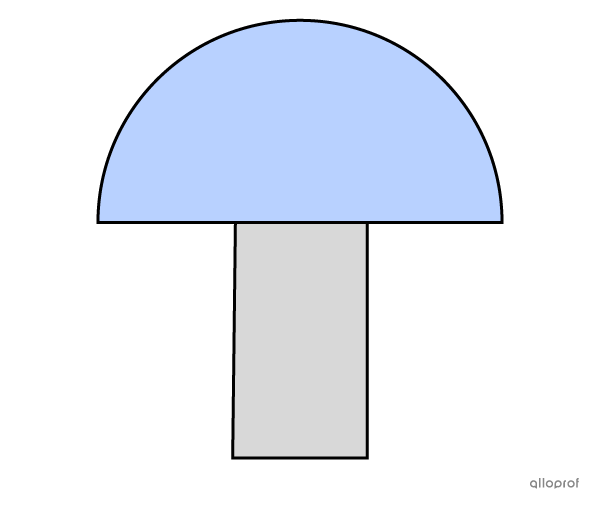
Find the total height of this figure using the following information:

The height of the rectangle measures |3\ \text{dm}| more than its base.
The measure of the diameter of the half-circle is triple the measure of the rectangle’s base.
The total area of this figure is |84.55\ \text{dm}^2.|

See solution

Word Problem

Example

With the opening of his new business, the owner of an ice cream shop wants to buy an advertising poster.

However, his budget limits him to the following constraints:

The area of the half-circle and the ice cream rim should be equal to |253\ \text{cm}^2.|
The area of the ice cream cone drawing and the rim of the ice cream should be equivalent to |276\ \text{cm}^2.|
The height of the cone must be |18\ \text{cm}.|
The height of the ice cream rim must be |4\ \text{cm}.|

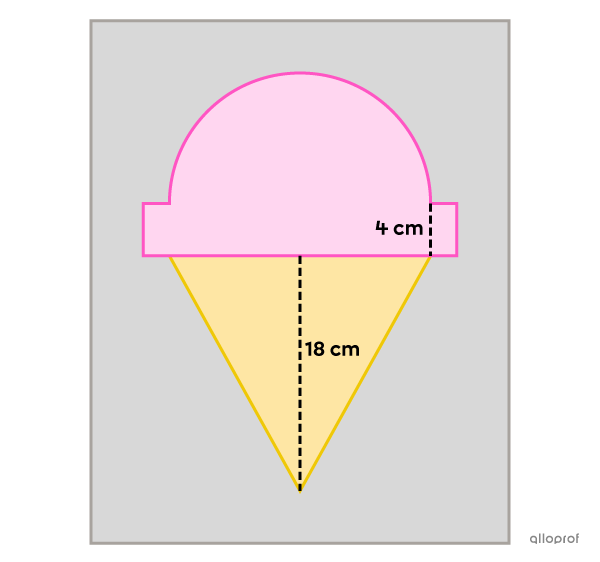
Decomposable figure representing an ice cream cone.

What must be the dimensions of the poster if the poster extends |4\ \text{cm}| beyond each end of the drawing?

See solution

See solution

See solution

See solution

Word Problem

See solution

See also