Finding Missing Measurements in Plane Figures by Solving a System of Equations

Concept sheet | Mathematics

Secondary

3-4

Top of page
Word Problems
See also

Sometimes we are looking for missing measurements in plane figures. To find them, you must solve a system of equations using the comparison method, substitution method or elimination method. You also need to know the perimeter and area formulas. Here are the steps to follow to do so.

Rule

Create a system of 2 equations using the information given in the problem.
Solve the system of equations.
Answer the question.

Here are a series of examples. The first are geometry problems that do not have a specific context, while the last 2 are word problems that present a short situation.

Example

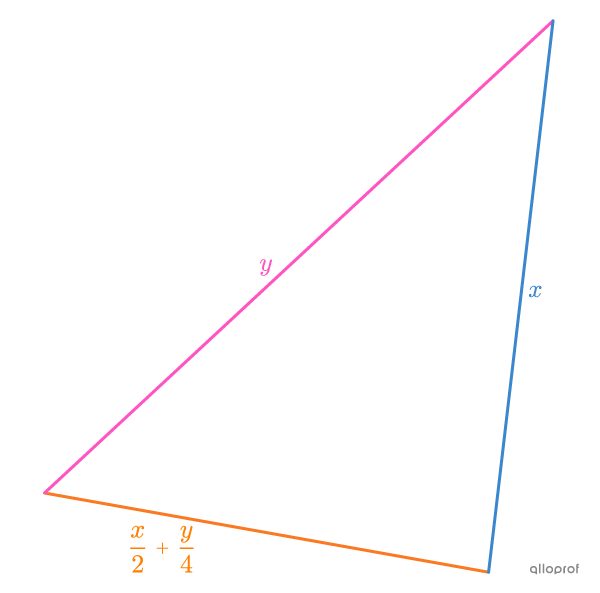
In the following triangle, |y| represents the longest side, |\dfrac{x}{2}+\dfrac{y}{4}| represents the shortest side and |x| represents the 3rd side.

Find the measure of each of the sides if the perimeter of the triangle is |49\ \text{cm}| and the length of the shortest side is |13\ \text{cm}.|

The measures of the sides of this triangle are sought from its perimeter.

See solution

Example

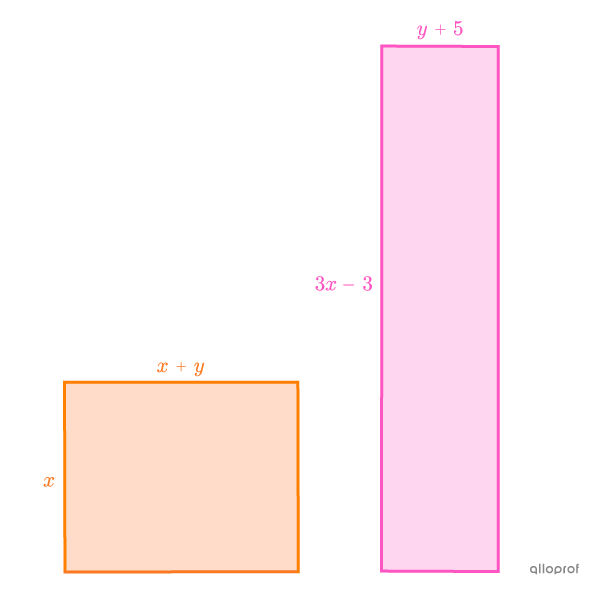
What is the measure of each of the sides of the 2 following rectangles if their respective perimeters are |58\ \text{cm}| and |88\ \text{cm}|?

The measure of the sides of these rectangles are sought using their perimeter.

See solution

Example

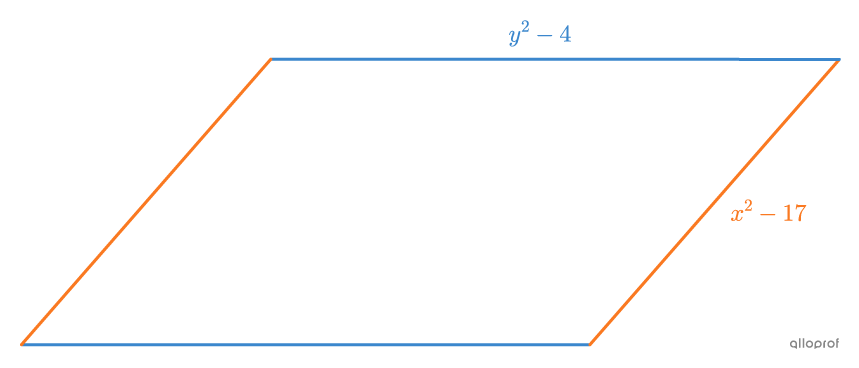
How long are the diagonals of the following 2 rhombuses if they have respective areas of |17.28\ \text{cm}^2| and |17.2\ \text{cm}^2|?

The measure of the sides of these rhombuses is sought using their area.

See solution

Example

What is the measure of the sides |\overline{AD},| |\overline{AB}| and |\overline{BC}| of the trapezoid if the total area of the trapezoid is |42\ \text{cm}^2| and the area of the triangular region is |6\ \text{cm}^2|?

The measures of this trapezoid’s sides are sought using its area.

See solution

Example

What is the measure of each side of the following parallelogram, if its perimeter is |40\ \text{cm}| and the measure of the shorter side is |\dfrac{2}{3}| the length of the longer side?

The measure of the sides of the parallelogram is sought using its perimeter.

See solution

Word Problems

Example

In an experimental setting, a company is trying to develop a new type of boomerang. To prevent people from getting hurt, a rubber band is installed around each end.

We are looking for the length of rubber needed for this boomerang.

What is the necessary length of rubber if we know that:

the arcs of the same colour are congruent to one another;
the perimeter of the toy is |38.16\ \text{cm};|
a convex arc of the circle is |1.4| times longer than a concave arc of a circle?

See solution

Example

For a Halloween party, a student decides to wear a ninja costume. In order not to break any school rules, he must make sure that his accessories are no longer than |10\ \text{cm}.|

To add authenticity to his costume, he decides to make a cardboard shuriken.

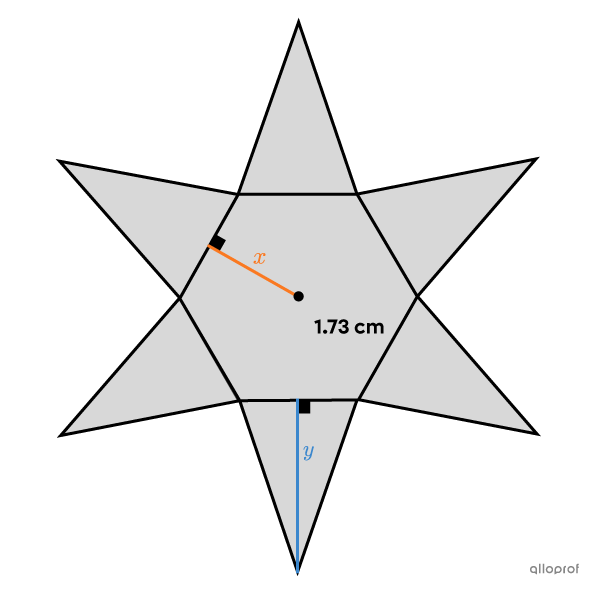
We want to know if this ninja star is longer than 10 cm.

According to his calculations, his stars should meet the following constraints.

Each star is formed by a regular hexagon encased by 6 congruent isosceles triangles.
The total area of each star is |20.74\ \text{cm}^2.|
The measure of the height of a triangle exceeds that of the apothem by |1\ \text{cm}.|

Based on this information, do the stars comply with school regulations?

See solution

See solution

See solution

See solution

See solution

Word Problems

See solution

See solution

See also