Subjects
Grades
The perimeter of any quadrilateral can always be determined by adding the measure of each side. The result is a length.
To determine the area of a quadrilateral, it is possible to use graph paper where each square has a specific area. By modifying the initial figure a little, the area of the quadrilateral can be determined.
By moving parts of the original quadrilateral, we can deduce the polygon has an area of |5\ \text{units}^2.|
It is possible to derive formulas for the perimeter and area specific to each quadrilateral based on their properties. The formulas are very useful for finding missing measurements.
Since the square is composed of 4 congruent sides and 4 right angles, we can derive formulas for the perimeter and area.
||\begin{align}P_\text{square}&=\color{#ec0000}a+\color{#3b87cd}b+\color{#3a9a38}c+\color{#fa7921}d\\
&=\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s\\
&=4\color{#3a9a38}s\end{align}||
Notice that the measure of one side of the square is the only information needed to calculate the perimeter.
To score a run in baseball, the player at bat must run to each base before finally returning to home plate. If a batter hits a homerun, the player can run the entire distance safely.
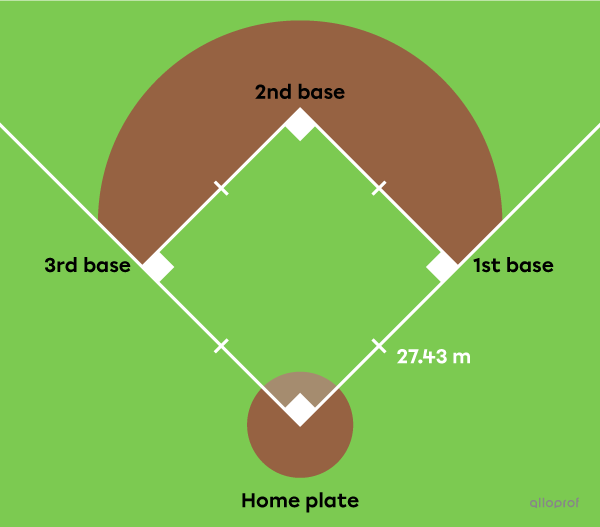
How far does a batter who hits a homerun have to travel before reaching home plate?
Just like calculating the perimeter, calculating the area of a square requires only the measure of one of its sides.
||\begin{align}A_\text{square}&=\color{#3a9a38}s\times \color{#3a9a38}s\\
&=\color{#3a9a38}s^2\end{align}||
where
|\color{#3a9a38}s:\text{side}|
A homeowner wants to know the surface area of his house’s floor because he plans to install hardwood.
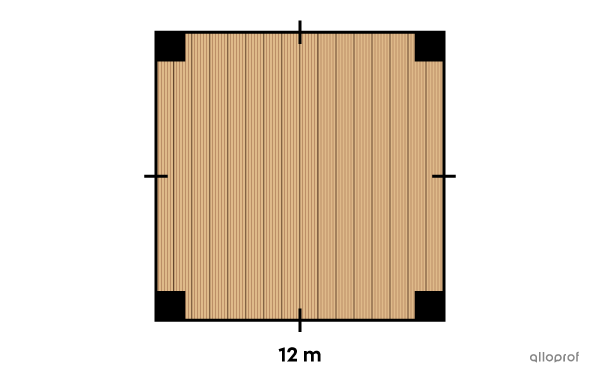
Does he have enough money with a budget of |\ $1\ 000| if the material desired costs
|\ $9.95/\text{m}^2?|
In a rectangle, the opposite sides are congruent and parallel. This property is useful when determining area and perimeter formulas.
||\begin{align}P_\text{rectangle}&=\color{#ec0000}a+\color{#3b87cd}b+\color{#3a9a38}c+\color{#fa7921}d\\
&= \color{#ec0000}h+\color{#ec0000}h+\color{#3b87cd}b+\color{#3b87cd}b\\
&=2\color{#ec0000}h+2\color{#3b87cd}b\\
&=2 (\color{#ec0000}h+\color{#3b87cd}b)\end{align}||
As shown in the previous box, the formula for the perimeter of a rectangle can be written several ways. Regardless of the formula chosen, the result is the same.
To install a border around his rectangular garden, Julian decides to install cement borders.
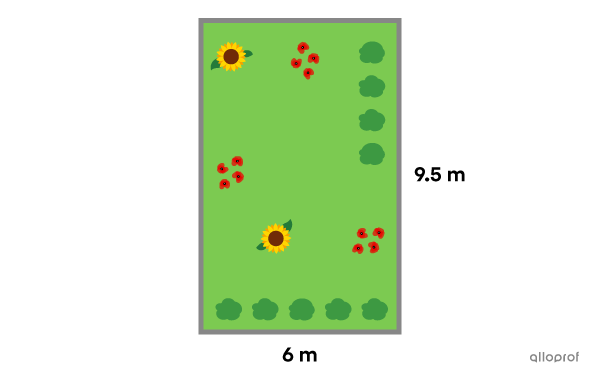
What is the cost of the installation if Julian knows a cement block of |90\ \text{cm}| in length costs |\$ 8.95?|
||A_\text{rectangle}=\color{#3b87cd}b\times\color{#ec0000}h||
where
|\color{#3b87cd}b:\text{base}|
|\color{#ec0000}h:\text{height}|
Note: As in the application of the perimeter formula, the dimensions of the base and the height are randomly assigned, as long as the 2 segments are perpendicular.
To change the decor of a room, Suzy decides to paint one of the rectangular walls sky blue.

How much will the change cost her if a can of paint is sold for |\ $39.95,| and one can of paint covers an area of |20\ \text{m}^2?| She must also apply 3 coats of paint.
Note: For problems related to the area of a figure, there is often more to do than just the calculation associated with the application of the formula. In such cases, it is important to understand the context of the problem.
The parallelogram's perimeter and area formulas are very similar to the rectangle’s.
||\begin{align}P_\text{parallelogram}&=\color{#3a9a38}a+\color{#3b87cd}b+\color{#ff55c3}c+\color{#fa7921}d\\
&=\color{#3a9a38}a+\color{#3b87cd}b+\color{#3a9a38}a+\color{#3b87cd}b\\
&=2\color{#3a9a38}a+2\color{#3b87cd}b\\
&=2(\color{#3a9a38}a+\color{#3b87cd}b)\end{align}||
As shown in the previous box, the formula for the perimeter of a parallelogram can be written in several ways. Regardless of the formula chosen, the result is the same.
Amélie runs in a park along a path that from a bird’s eye view forms a parallelogram. Her average running speed is |6\ \text{min/km}.| If she starts in front of the big tree and ends at the same spot, how long does her run last?

||A_\text{parallelogram}=\color{#3b87cd}b\times \color{#ec0000}h||
where
|\color{#3b87cd}b:\text{base}|
|\color{#ec0000}h: \text{height}|
The area formula for a parallelogram is the same as a rectangle’s. To demonstrate it, simply grab a part of the parallelogram and move it to form a rectangle.
Note: The measure of the other pair of congruent sides |(\color{#3a9a38}a)| is not used in the area formula.
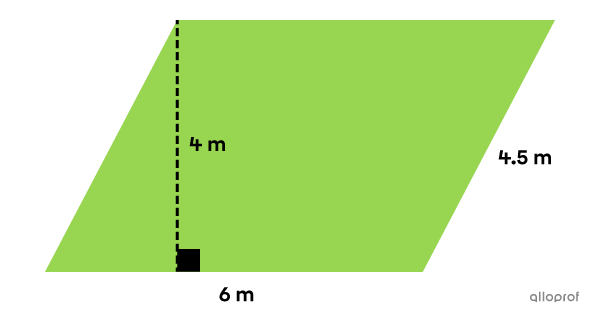
What is the area of the following parallelogram?
The area of a trapezoid, whether it is right-angled, isosceles, or otherwise, is always calculated with the same formula. However, the formula for the perimeter of a trapezoid can be tailored to the specific trapezoid.
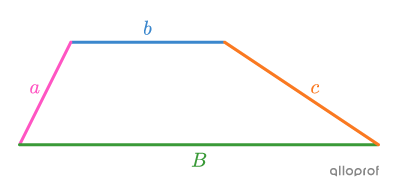
Trapezoid
||P_\text{trapezoid}= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c||
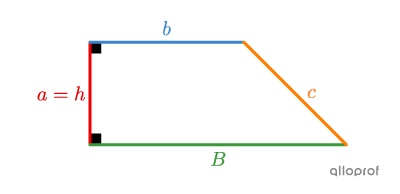
Right trapezoid
||\begin{align}P_\text{right trapezoid}&= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\&= \color{#ec0000}h+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\end{align}||

Isosceles trapezoid
||\begin{align}P_\text{isosceles trapezoid}&= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\ &= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#ff55c3}a\\ &= 2\color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B\end{align}||
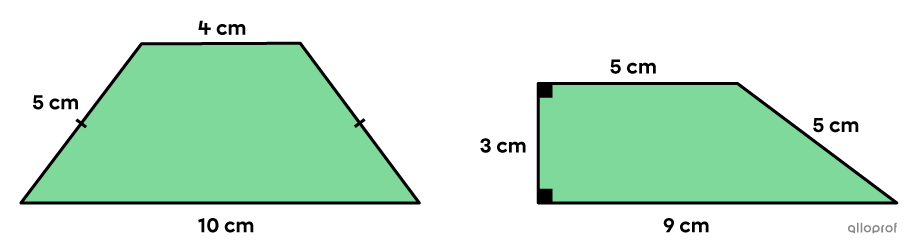
Which one of the following trapezoids has the largest perimeter?
||A_\text{trapezoid}=\dfrac{(\color{#3a9a38}{B}+\color{#3b87cd}b)\times\color{#ec0000}h}{2}||
where
|\color{#3a9a38}B:\text{large base}|
|\color{#3b87cd}b:\text{small base}|
|\color{#ec0000}h:\text{height}|
To distinguish between each of the measurements used in the formula, refer to the properties of trapezoids. Note that the height always represents the distance measured perpendicular to the 2 bases.
To prove the formula, we use geometric transformations on some portions of a trapezoid to form a rectangle.
By doing so, we create a rectangle where the length is |\color{#3b87cd}b+\color{#3a9a38}B| and the height |\color{#ec0000}h| is the same as a trapezoid’s. Since the rectangle is composed of 2 trapezoids, we must divide by 2 to obtain the area of a trapezoid.
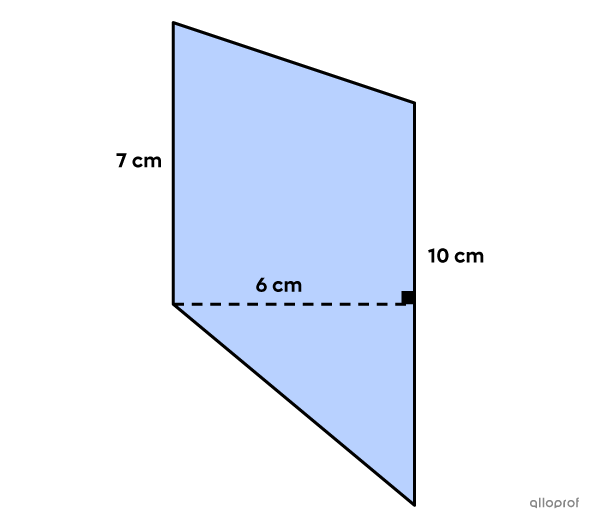
What is the area of the following trapezoid?
||\begin{align}P_\text{rhombus}&=\color{#ff55c3}a+\color{#C58AE1}b+\color{#3a9a38}c+\color{#fa7921}d\\
&=\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s\\
&=4\color{#3a9a38}s\end{align}||
Only one measure is needed to calculate the perimeter of a rhombus.
What is the perimeter of the following rhombus?

||A_\text{rhombus}=\dfrac{\color{#3b87cd}D\times\color{#ec0000}d}{2}||
where
|\color{#ec0000}d:\text{small diagonal}|
|\color{#3b87cd}D:\text{large diagonal}|
The formula for the area of a rhombus is related to the formula for the area of a rectangle. We can use a rotation to create a rectangle from a rhombus.
A rectangle is obtained with the area given by the following formula.
||\begin{align}A&=\color{#3b87cd}b\times\color{#ec0000}h\\
&=\color{#3b87cd}D\times\color{#ec0000}d\end{align}||
The rectangle is composed of 2 rhombuses. We must therefore divide the area of the rectangle by |2| to obtain the area of one rhombus.
||A_\text{rhombus}=\dfrac{\color{#3b87cd}D\times\color{#ec0000}d}{2}||
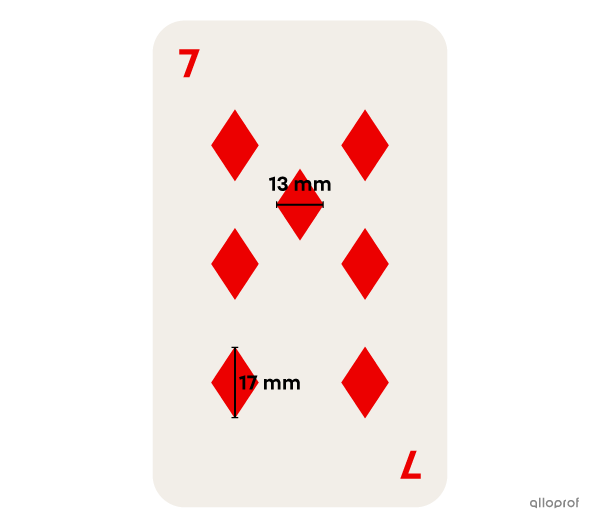
Theo has lost a card from his favorite deck of cards. It was the 7 of diamonds. Since he has a white card and some red paint, he decides to make a new card to replace it. The diamonds he paints are rhombi, all the same size. Given that one milliliter covers about |180\ \text{mm}^2,| how much paint will he need?
||\begin{align}P_\text{kite}&=\color{#3a9a38}a+\color{#fa7921}b+\color{#ff55c3}c+\color{#C58AE1}d\\
&=\color{#3a9a38}a+\color{#3a9a38}a+\color{#fa7921}b+\color{#fa7921}b\\
&=2\color{#3a9a38}a+2\color{#fa7921}b\\
&=2(\color{#3a9a38}a+\color{#fa7921}b)\end{align}||
As illustrated in the previous box, the formula for the perimeter of the kite can be written in several ways. No matter which formula is chosen, the result is the same.
To protect the edges of a new kite, we want to buy plastic trim.

What is the total cost of the project if the material sells for |$1.95| per |10\ \text{cm?}|
||A_\text{kite}=\dfrac{\color{#ec0000}D\times \color{#3b87cd}d}{2}||
where
|\color{#ec0000}D:\text{large diagonal}|
|\color{#3b87cd}d:\text{small diagonal}|
The area formula of a kite is related to the rectangle's area formula. To understand where the formula comes from, refer to the proof of the formula for the area of a rhombus.
With changing weather conditions, a kite needs a new layer of water repellent for its surface so water won’t damage it.
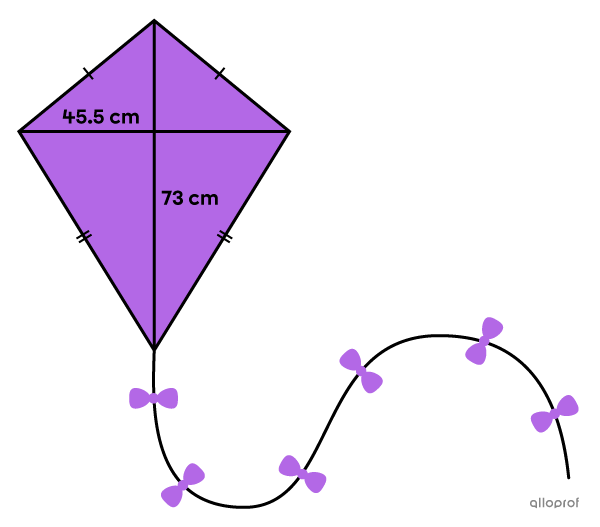
Assuming that both sides of the kite must be treated, how much product should be purchased if |10\ \text{mL}| can cover an area of |1\ \text{dm}^2?|