Subjects
Grades
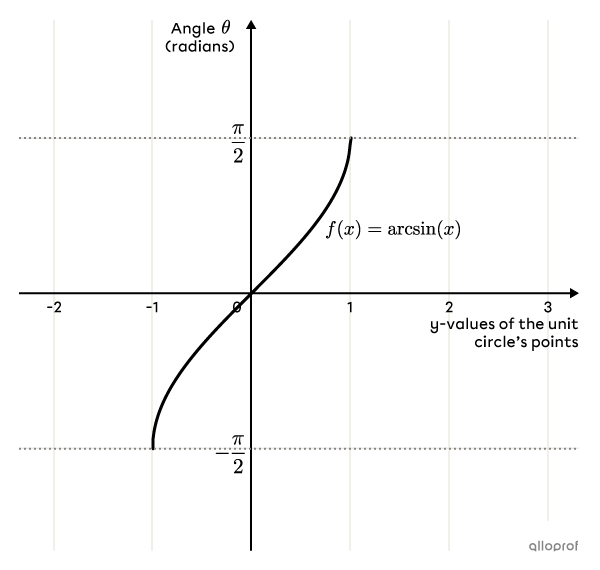
The inverse of the basic sine function is the arcsine function. The arcsine function relates the measure of the angles (in radians) of the unit circle with the |y|-values of the circle’s points.
The rule of the basic arcsine function is |f(x)=\arcsin (x).| The function can also be written |f(x)=\sin^{-1}(x).|
Note: Do not confuse the notation |\sin^{-1}(x)| with |\dfrac{1}{\sin (x)}.|
Properties of the |\arcsin (x)| function:
The function passes through the origin of the Cartesian plane.
The domain of the function is |[-1,1].|
The range (codomain) is |\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right].|
The function is increasing over its domain.
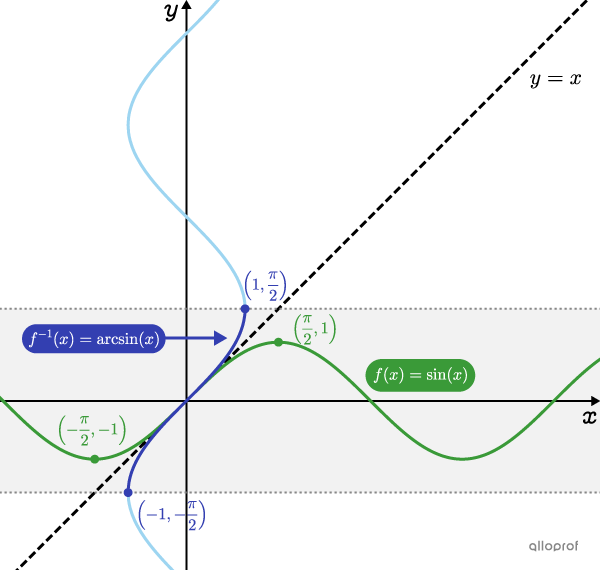
The inverse of a sine function is not a function. To become one, its range must be restricted.
The basic sine function is shown on the following Cartesian plane. To graph the inverse, exchange the |x|- and |y|-coordinates of the function’s points. A reflection of the points can also be conducted relative to the line |y=x.| For example, point |\left(\dfrac{\pi}{2},1\right)| becomes point |\left(1,\dfrac{\pi}{2}\right)\!.|
Another curve is then obtained that is not a function. Restricting the range of the inverse to the interval |\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\!,| produces the arcsine function.
Follow the steps below to find the rule for the inverse of a sine function.
Interchange |x| and |y| in the rule.
Isolate the |y| variable.
Give the inverse rule.
Determine the rule for the inverse of the function |f(x)=-2\sin\left(\dfrac{1}{3}(x-\pi)\right)-5.|
Interchange |x| and |y| in the rule
||\begin{align}\color{#3B87CD}y&=-2\sin\left(\dfrac{1}{3}(\color{#FF55C3}x-\pi)\right)-5\\ \color{#FF55C3}x&=-2\sin\left(\dfrac{1}{3}(\color{#3B87CD}y-\pi)\right)-5\end{align}||
Isolate the |y| variable
||\begin{align}x&=-2\sin\left(\dfrac{1}{3}(\color{#3B87CD}y-\pi)\right)-5\\x+5&=-2\sin\left(\dfrac{1}{3}(\color{#3B87CD}y-\pi)\right)\\ \dfrac{x+5}{-2}&=\sin\left(\dfrac{1}{3}(\color{#3B87CD}y-\pi)\right)\end{align}||
To isolate |y,| eliminate |\sin| by performing the inverse operation, |\sin^{-1}.|
||\begin{align}\color{#EC0000}{\sin^{-1}\!\left(\color{black}{\dfrac{x+5}{-2}}\right)}&=\dfrac{1}{3}(\color{#3B87CD}y-\pi)\\3\sin^{-1}\!\left(\dfrac{x+5}{-2}\right)&=\color{#3B87CD}y-\pi\\3\sin^{-1}\!\left(\dfrac{x+5}{-2}\right)+\pi&=\color{#3B87CD}y\end{align}||
It is possible to simplify by working within the brackets. In fact, dividing by |-2| can also be written as multiplying by |-\dfrac{1}{2}.|||\begin{align}3\sin^{-1}\!\left(\color{#EC0000}{\dfrac{x+5}{-2}}\right)+\pi&=y\\ 3\sin^{-1}\!\left(\color{#EC0000}{-\dfrac{1}{2}(x+5)}\right)+\pi&=y\end{align}||
Give the inverse rule
The inverse rule of the sine function is the following.
||f^{-1}(x)=3\sin^{-1}\!\left(-\dfrac{1}{2}(x+5)\right)+\pi||
Note: For the inverse to become a function, its range must be restricted.
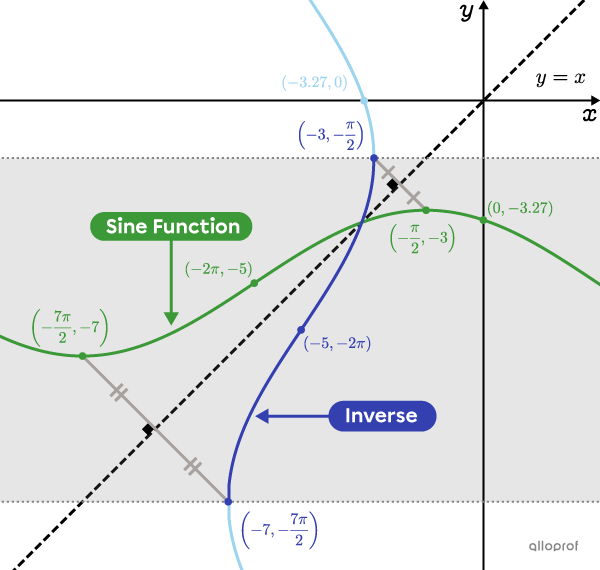
See the following graphical representation of the sine function from the previous example, where the rule is |f(x)=-2\sin\left(\dfrac{1}{3}(x-\pi)\right)-5.|
For the inverse to become a function, its range must be restricted. In the following example, the range must be restricted to the interval |\color{#333fb1}{\left[-\dfrac{7\pi}{2},-\dfrac{\pi}{2}\right]}.|