Subjects
Grades
The Net and Drawing of a Sphere
Concept sheet | Mathematics
Secondary
3
Table of contents
Because their surfaces consist entirely of curves, spheres are geometric shapes that cannot be perfectly broken down into two dimensions (2-D).
A sphere is the surface (area) consisting of the cluster/locus of points located at the same distance from a point, called the “centre.”
On the other hand, the interior of a sphere refers to the space (volume) occupied by the sphere.
Even so, we can try to approximate its net based on the formula for its surface area.
The Net of a Sphere
As explained above, it is impossible to break down a sphere perfectly into a 2-D form. However, we can associate its net with those of several circles.
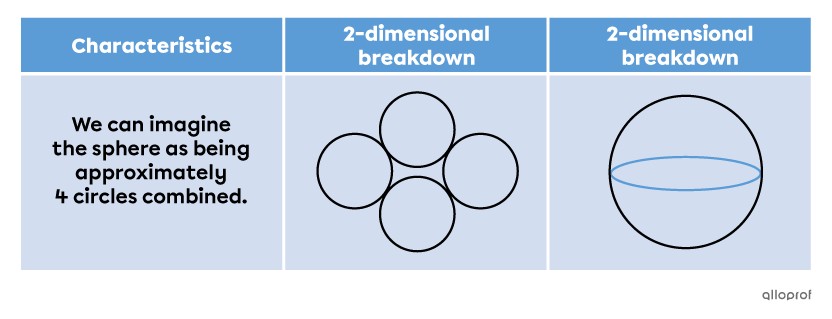
This estimation can be understood by comparing the formulas for the area of a circle and a sphere.
||\begin{align} Area_{circle}&=\pi r^{2}\\
Area_{sphere}&=4\pi r^{2}\end{align}||
Notice that:
||\begin{align}Area_{sphere}&=4\times(\pi r^{2})\\
&=4\times Area_{circle}\end{align}||
which explains the approximation of the sphere's net into 4 circles.
How to Draw a Sphere
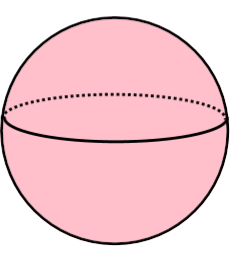
To do this, we base ourselves on its circular appearance, then add a few details to emphasize its three-dimensional aspect.
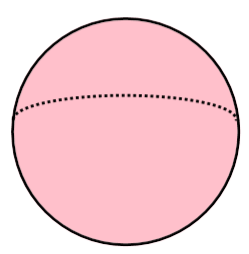
1. Draw a circle using a compass.
2. Add depth by drawing a dotted half-ellipse curving towards the back of the sphere.
3. Finish the depth effect by drawing the same half-ellipse with a solid line curving forward.
