Subjects
Grades
The Trigonometric Ratio of Cosine
Concept sheet | Mathematics
Secondary
4
Table of contents
The cosine ratio is one of the 3 main trigonometric ratios found in a right triangle.
In a right triangle, the cosine of an angle |(\boldsymbol \theta)| is the ratio between the length of the leg that is adjacent to the angle and the hypotenuse.||\cos \theta=\dfrac{\text{leg $\color{#333fb1}{\text{adjacent }}$to angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}||
If we want to determine the cosine of the acute angles in the following right triangle, we get 2 ratios.
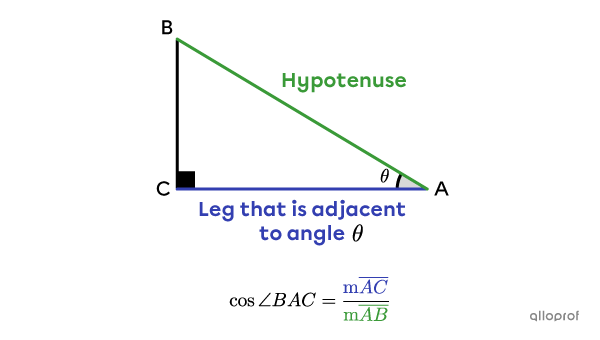
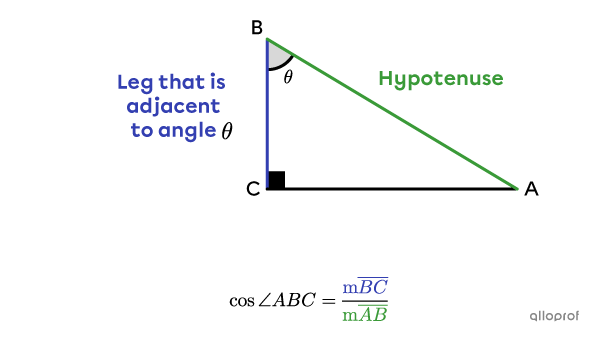
The cosine trigonometric ratio is only used with respect to the acute angles of a right triangle. The cosine is never sought in relation to the right angle.
Finding the length of a side using the |\boldsymbol\cos| trigonometric ratio
Finding the length of a leg using the |\boldsymbol\cos| ratio
To find the length of a leg of a right triangle using the cosine ratio, the length of the hypotenuse and the measure of the angle adjacent to the side in question must be known.
Find the length of side |\overline{BC}| using the cosine ratio in the following right triangle.
See solution
For greater accuracy, do the calculations in one step on a calculator. If this is not possible, keep at least 3 to 4 digits after the decimal point.
Here is an example when |\theta=65^{\circ}| and the hypotenuse measure |59\ \text{cm}.|
Performing the calculation in one step
||\begin{align}\cos65^{\circ}&=\dfrac{a}{{59}}\\\cos65^{\circ}\times59&=a\\\color{#EC0000}{24.93}&\approx a\end{align}||
Performing the calculation in 2 steps
||\begin{align}\cos65^{\circ}&=\dfrac{a}{59}\\\color{#ec0000}{0.42}&\approx\dfrac{a}{59}\\0.42\times59&\approx a\\\color{#EC0000}{24.78}&\approx a\end{align}||
If the calculations are performed in 2 steps, and we only round to 2 decimal places when calculating the cosine of the angle, there will be a difference of 15 hundredths compared to the correct answer.
In some cases, neither the length of the hypotenuse nor the length of the side adjacent to the angle are known. In order to apply the cosine ratio, the measure of the other angle has to be determined.
Use the cosine ratio to determine the length of the leg sought in the following right triangle.
See solution
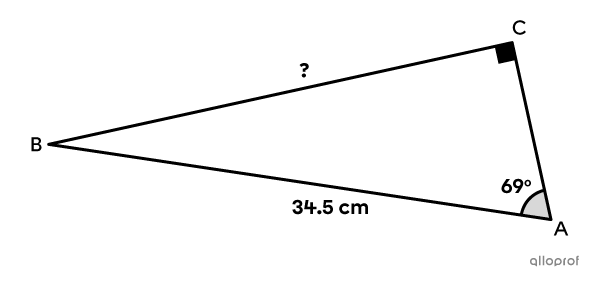
In the previous example, the sine trigonometric ratio could have been used to find the length of side |\overline{BC}| using the |69^{\circ}| angle. The answer would have been the same.
Finding the length of the hypotenuse using the |\boldsymbol\cos| ratio
To find the length of the hypotenuse in a right triangle using the cosine ratio, the measure of one acute angle and the length of the side adjacent to it must be known.
Find the length of the hypotenuse using the cosine ratio in the following right triangle.
See solution
The cosine ratio with a |\boldsymbol{60^{\circ}}| angle
In a right triangle, the length of the leg adjacent to a |60^{\circ}| angle is always equal to half the length of the hypotenuse.
This means the cosine ratio is always |\dfrac{1}{2}.|||\begin{align}\cos60^{\circ}&=\dfrac{\text{leg $\color{#333fb1}{\text{adjacent}}$ to angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}\\&=\dfrac{\frac{\color{#3A9A38}c}{2}}{\color{#3A9A38}c}\\&=\dfrac{1}{2}\end{align}||
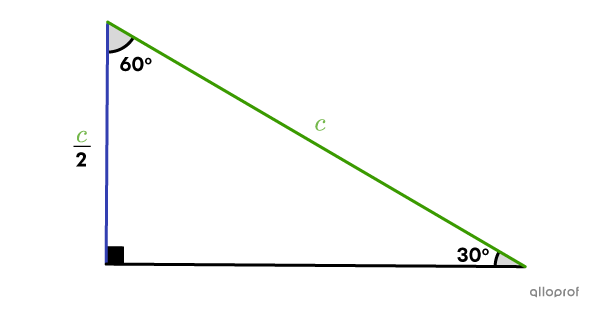
What is the length of side |\overline{AB}| in the following triangle?
See solution
Finding an angle measure using |\boldsymbol{\cos^{-1}}|
To find the measure of an acute angle in a right triangle using the cosine ratio, the length of the side adjacent to it and the length of the hypotenuse must be known. This is essentially the same as answering the following question: “What angle gives a cosine of...?”
First, determine the cosine ratio, then use the |\cos^{-1}| key (also called |arccos| ) on a calculator.
Find the measure of angle |BAC| in the following right triangle using the cosine ratio.
See solution
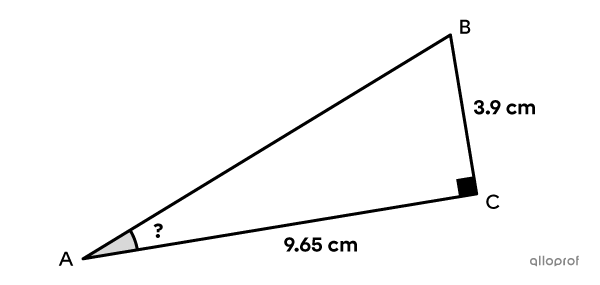
In trigonometry, there are several possible ways to get the same answer. In the previous example, we could have used |\boldsymbol{\tan^{-1}}| with respect to angle |BAC,| which would have given the measurement directly.
The arccosine function (denoted |\cos^{-1}(x)| ) is the inverse of the cosine function.||\cos \theta=x\ \Leftrightarrow \ \cos^{-1}x=\theta||