Subjects
Grades
Ohm's Law
Concept sheet | Science and Technology
Secondary
4
Table of contents
Ohm's law relates the potential difference, resistance and current intensity in an electrical circuit.
|V=RI|
where
|V:| potential difference in volts |\text{(V)}|
|R:| resistance in ohms |(\Omega)|
|I:| electric current intensity in amperes |\text{(A)}|
From the previous formula, we can establish the following three relationships.
-
If |R| is constant and |I| increases, then |V| increases.
-
If |I| is constant and |R| increases, then |V| increases.
-
If |V| is constant and |R| increases, then |I| decreases.
Here is a graph of the potential difference as a function of current intensity.
Move the sliders to change the current intensity or the resistance.
In the previous graph, we can see that:
-
when the current intensity increases, the potential difference increases proportionally;
-
the rate of change (slope) corresponds to the resistance;
-
the higher the resistance, the steeper the slope.
Calculation Examples
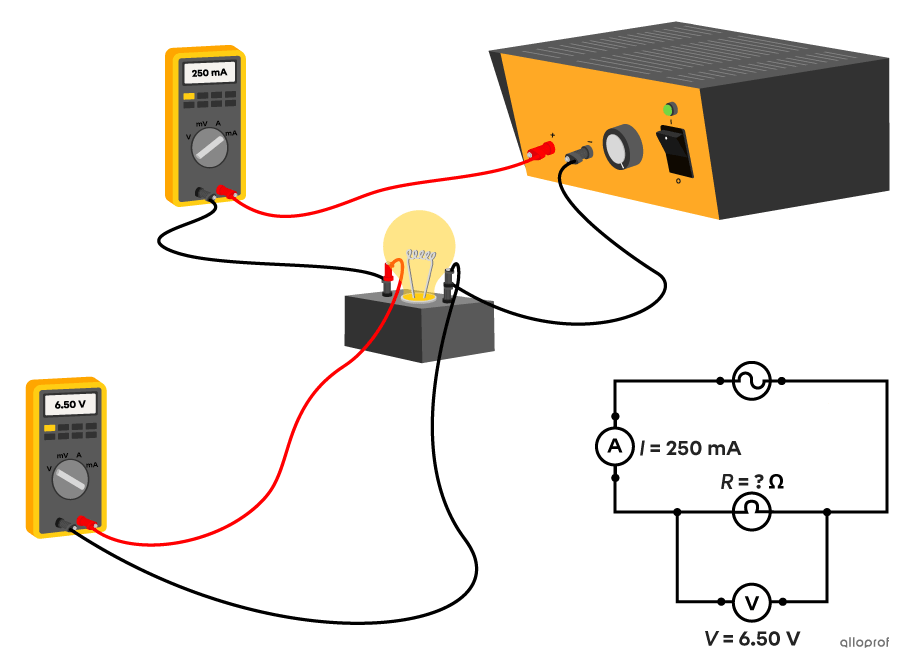
In the lab, we have an electrical circuit consisting of a power supply and a light bulb.
We add an ammeter connected in series and a voltmeter connected in parallel with the light bulb.
The ammeter measures a current intensity of |250\ \text{mA}.| The voltmeter measures a potential difference of |6.50\ \text{V}.|
What is the resistance of the light bulb?
See solution
The electrical circuit of a remote control toy has a resistance of |120\ \Omega.| If it is designed for an electrical current intensity of |0.05\ \text{A},| what potential difference must the toy's battery provide?
See solution
A smartphone uses a |3.7\ \text{V}| battery. If the internal circuit resistance is |18.5\ \Omega,| what is the current intensity in milliampere |(\text{mA})| flowing through the circuit?