Matières
Niveaux
Les rapports de similitude, d'aires et de volumes (k, k², k³)
Fiche | Mathématiques
Lorsque 2 figures planes sont semblables, il existe un rapport de similitude entre leurs côtés homologues (k) et leur aire (k²). Lorsque 2 solides sont semblables, il existe un rapport de similitude entre leurs arêtes homologues (k), leurs faces homologues (k²) et leur volume (k³).
Chacun de ces rapports peut être utilisé pour trouver une mesure manquante dans une figure ou une mesure manquante dans un solide.
Les rapports de similitude, d’aires et de volumes indiquent soit un agrandissement ou une réduction de la figure image par rapport à la figure initiale.
Si la figure image est plus grande que la figure initiale, alors :||k=\dfrac{\color{#333fb1}{\text{Figure image}}}{\color{#3a9a38}{\text{Figure initiale}}}=\dfrac{\color{#333fb1}{\text{Grande figure}}}{\color{#3a9a38}{\text{Petite figure}}}||où |k>1|
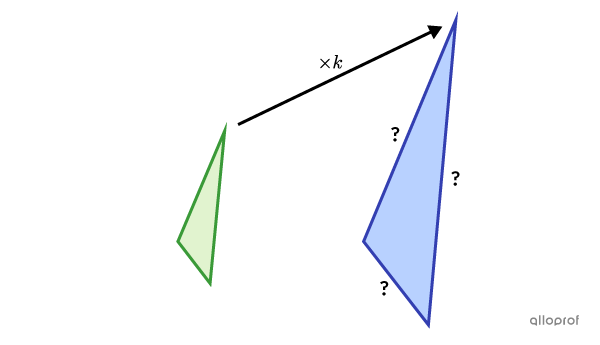
Dans ce cas-ci, on dit que |k| est un rapport d’agrandissement.
Si la figure image est plus petite que la figure initiale, alors :||k=\dfrac{\color{#333fb1}{\text{Figure image}}}{\color{#3a9a38}{\text{Figure initiale}}}=\dfrac{\color{#333fb1}{\text{Petite figure}}}{\color{#3a9a38}{\text{Grande figure}}}||où |0<k<1|
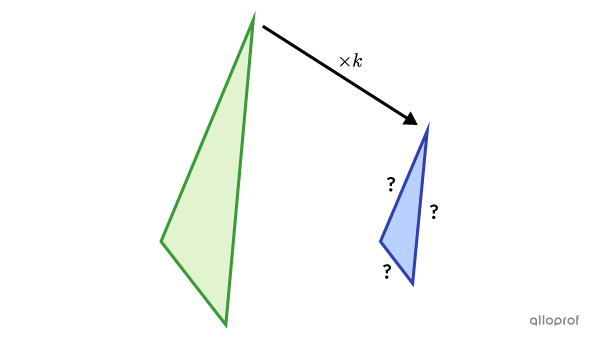
Dans ce cas-ci, on dit que |k| est un rapport de réduction.
Les rapports de similitude, d’aires et de volumes ne sont valides que si l’on compare des longueurs, des aires ou des volumes homologues. Par exemple, il ne faut pas comparer la hauteur d’une pyramide avec l’apothème d’une autre pyramide, puisque la hauteur et l’apothème ne sont pas des segments homologues.
Le rapport de similitude (k)
Le rapport de similitude |\boldsymbol{(k)}| est un rapport entre des longueurs homologues (côtés, périmètres, rayons, circonférences, etc.) de 2 figures semblables.
||k=\dfrac{\text{Longueur dans la figure image}}{\text{Longueur homologue dans la figure initiale}}||ou||k=\dfrac{\text{Longueur dans le solide image}}{\text{Longueur homologue dans le solide initial}}||
Le rapport des aires (k²)
Le rapport des aires |\boldsymbol{(k^2)}| est un rapport entre des surfaces homologues (aires de figures planes, bases de prismes, faces latérales de pyramides, etc.) de 2 figures semblables.
||k^2=\dfrac{\text{Aire de la figure image}}{\text{Aire de la figure initiale}}||ou||k^2=\dfrac{\text{Face dans le solide image}}{\text{Face homologue dans le solide initial}}||
Le rapport des volumes (k³)
Le rapport des volumes |\boldsymbol{(k^3)}| est un rapport entre les volumes de 2 solides semblables.
||k^3=\dfrac{\text{Volume du solide image}}{\text{Volume du solide initial}}||
Exercice
Les relations entre les rapports k, k² et k³
L’outil interactif suivant permet d’observer ce qui se produit avec les longueurs, les aires et le volume en changeant la valeur de |k.|
-
Combien de fois le segment vert entre-t-il dans le segment bleu?
-
Combien de fois le carré vert entre-t-il dans le carré bleu?
-
Combien de fois le cube vert entre-t-il dans le cube bleu?
Voir la solution
Lorsqu’on connait la valeur d’un des 3 rapports, il est possible de déduire la valeur des 2 autres à l’aide des propriétés des exposants et des racines. Le schéma suivant résume les opérations nécessaires pour passer d’un rapport à l’autre.
Pour assurer une utilisation optimale et juste de ce schéma, il faut absolument suivre le sens des flèches. Par exemple, pour passer de |k^3| à |k^2,| il est nécessaire de suivre le chemin |k^3\rightarrow k\rightarrow k^2.|
Les rapports de similitude (k, k², k³)
Voici comment procéder lorsqu’on cherche des mesures manquantes à l’aide de |k,| |k^2| et |k^3.|
-
Identifier le rapport qui permet de trouver la mesure manquante.
-
Calculer le rapport qui permet de trouver la mesure manquante à l’aide des relations entre les rapports.
-
Calculer la mesure manquante.
Exercice
Résoudre un problème impliquant k, k² et k³
Les 2 solides semblables suivants sont des polyèdres réguliers nommés octaèdres.
Trouve la mesure des arêtes et le volume de l’octaèdre orange et de l’octaèdre bleu pâle.
Voir la solution
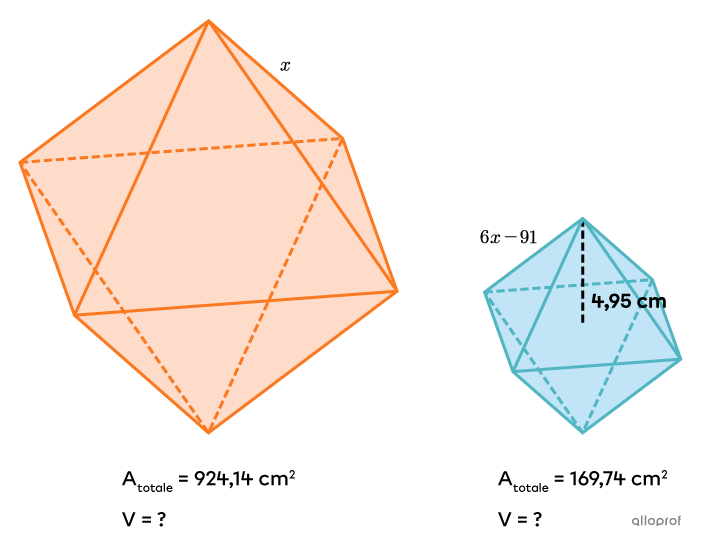
Dans l’exemple précédent, la valeur de |k^3| utilisée pour calculer le volume de l’octaèdre orange indique qu’il s’agit d’un rapport de réduction |\left(0<\dfrac{27}{343}<1\right).| Puisque l’octaèdre orange est plus gros que l’octaèdre bleu pâle, il aurait aussi été possible d’utiliser l'inverse de |\dfrac{27}{343}| afin d’utiliser un rapport d’agrandissement. La démarche aurait alors été la suivante.||\begin{align}\dfrac{1}{k^3}&=\dfrac{\color{#fa7921}{\text{Volume de l'octaèdre initial}}}{\color{#51b6c2}{\text{Volume de l'octaèdre image}}}\\\dfrac{343}{27}&=\dfrac{\color{#fa7921}V}{\color{#51b6c2}{161{,}7}}\\343\times161{,}7&=V\times27\\\color{#ec0000}{\dfrac{\color{black}{343\times161{,}7}}{27}}&=\color{#ec0000}{\dfrac{\color{black}{V\times27}}{27}}\\2\ 054{,}19\ \text{cm}^3&\approx V\end{align}||