Best Of
Re: Question
Merci pour ta question!
Je te félicite pour ton initiative d'étudier les concepts difficiles à l'avance!
D'abord, examinons la formule elle-même :
$$ n = \frac{m}{M} $$
Légende :
• n : nombre de moles
• m : masse
• M : masse molaire
Essentiellement, cette formule stipule qu'on peut trouver le nombre de moles dans une certaine masse en la divisant par la masse molaire de la substance. Cette formule est légèrement plus intuitive si on indique les unités :
$$ moles = \frac{grammes}{grammes / mole} $$
$$ moles = moles $$
On constate que les unités de masse s'annulent pour donner un nombre de moles.
Ensuite, il est aussi important de comprendre qu'on peut modifier la formule selon nos besoins avec des multiplications et divisions :
$$ n = \frac{m}{M} $$
$$ M\times n = \frac{m}{M} \times M $$
$$ Mn = m $$
Ou encore :
$$ n = \frac{m}{M} $$
$$ n÷m = \frac{m}{M} ÷ m $$
$$ \frac{n}{m} = \frac{1}{M} $$
$$ \frac{m}{n} = M $$
Maintenant, pour répondre plus précisément à ta question sur l'application de la formule, je crois qu'il est important d'établir ce qu'on sait et ce qu'on cherche au début d'un problème. Tu peux établir une liste des variables que tu connais, et une liste des variables que tu cherches. Par exemple, si tu as deux sur trois des variables dans la formule, tu peux utiliser la formule pour retrouver la valeur de la troisième. Tu peux réarranger la formule afin qu'elle te donne la réponse directement aussi.
Cette fiche du site d'Alloprof explique le concept de mole :
N'hésite pas si tu as d'autres questions!
Re: Question
Salut !
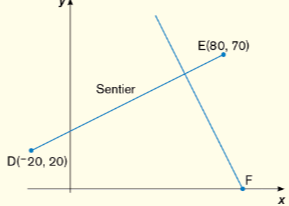
Tu sembles avoir omis une information capitale qui indique que le point F est sur l'abscisse.
La première étape est de trouver la règle de la droite DE.
Puis, tu trouve le point de partage à 4/5 du sentier.
$$ (x_{\small{P}},y_{\small{P}})=\big(x_1+k(x_2-x_1),y_1+k(y_2-y_1)\big) $$
Par la suite, avec ce point et sachant que DE et perpendiculaire à la droite où se trouve F, tu peux calculer la règle de la fonction du nouveau sentier.
Finalement, tu trouver la valeurs de l'abscisse à l'origine F et tu calcules les distances.
$$ \text{dist}(A,B)=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Salut !
Le titre d'un tableau est en effet important.
Il te faut aussi penser que tu n'as pas besoin de répéter tous tes titres de colonnes dan ton titre. Tu peux utiliser un titre simple comme "Données et rendement de la réaction de ... avec ...". Tu permet ainsi d'identifier la réaction sans effectuer de répétitions.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Question
Bonjour est ce que si il y a une personne qui peut maider pour les addition et soustraction debout il peux me répondre sil vous plait car jai une situation problème la semaine prochaine
Re: Question
Bonjour!
Cette expression est, en fait, un anglicisme. Il s'agit d'un calque de l'expression anglaise « heart skips a beat ». En français, on pourrait dire que le coeur fait un bon, par exemple.
J'espère t'avoir aidé! Si tu as d'autres questions, n'hésite pas à nous réécrire! :D
Laurie :)
Re: Question
Salut !
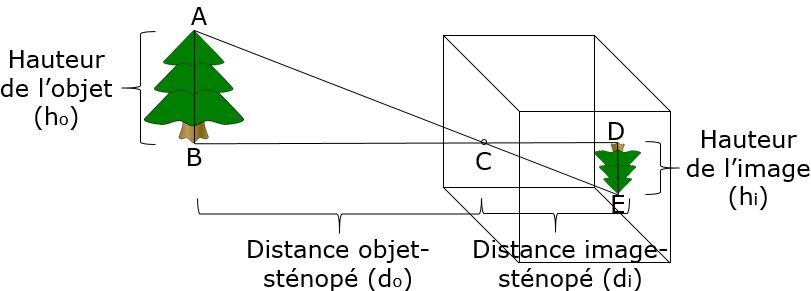
Le grandissement est toujours positif selon la convention des signes. Dans le cas de la sténopé, on ne regarde que la relation de manière mathématique comme les deux triangles rectangles formant le trajet optiques sont semblables.
Toutefois, même en utilisant la convention des signes, la valeur de grandissement est positive.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Bonjour FraiseAdorable,
Merci pour ta question!
Malheureusement, l'équipe d'Alloprof ne peut pas corriger tes exercices. Je t'invite à nous réécrire si tu éprouves une difficulté ciblée dans un problème:)
Bonne soirée!
Kylan
Re: Question
k(x) = a[-0.1(x + 5)] - 10.5
l'ordonnée à l'origine vaut -9 (c'est la valeur de y quand x = 0) => -9 = a[-0.1(0 + 5)] - 10.5 => -9 = a[-0.5] - 10.5
or [-0.5] est le plus grand entier inférieur ou égal à -0.5, c'est donc -1
=> -9 = -a - 10.5 => a = 9 - 10.5 = -1.5
et la fonction k est définie par
k(x) = -1.5[-0.1(x + 5)] - 10.5
On veut savoir pour quelles valeurs de x k(x) = 9
9 = -1.5[-0.1(x + 5)] - 10.5
-19.5/1.5 =[-0.1(x + 5)]
-13 = [-0.1(x + 5)]
si x = 120 on a [-0.1(x + 5)] = [-12.5] = -13
si x = 125 on a ....
si x = 115 on a ....
Re: Question
Salut!
Voici le répertoire de révision présentant toutes les notions étudiées en 6e année du primaire en mathématiques : Répertoire de révision | Mathématiques — 6e année primaire | Primaire | Alloprof
Bonne étude! :)
Re: Question
Bonjour Bleuet !
Voici une fiche d'alloprof sur tous les notions en mathématiques de 6ème année :
N'hésite pas à nous poser des questions si tu as des doutes :D
Bonne journée !