Best Of

Salut!

Voici un début de démarche alternative possible :

$$ 80 000(\frac{1}{2})^n < 0,02(2)^n$$

Tu peux commencer par éliminer le facteur 0,02 :

$$\frac{80 000(\frac{1}{2})^n}{0,02} <\frac{0,02(2)^n}{0,02}$$

$$ 4 000 000(\frac{1}{2})^n < 2^n$$

Ensuite, on place la variable du même côté :

$$ 4 000 000(\frac{1}{2})^n < 2^n$$

$$ 4 000 000 < \frac{2^n}{(\frac{1}{2})^n}$$

Finalement, rappelle-toi que (1/2) = 2^-1 et qu'une division de bases identiques permet une soustraction des exposants :

$$ 4 000 000 < \frac{2^n}{(2^{-1})^n} $$

$$ 4 000 000 < \frac{2^n}{2^{-n}} $$

$$ 4 000 000 < 2^{n--n} $$

$$ 4 000 000 < 2^{2n} $$

À ce stade, tu peux poursuivre la résolution avec ces indices. N'hésite pas à revenir vers nous au besoin :)

Allo GalaxieSigma4570,

Merci pour ta question!

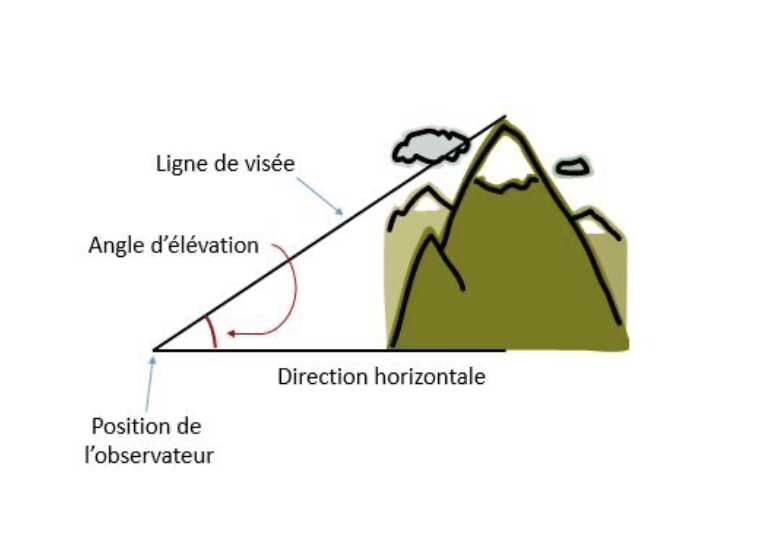
Ici, on cherche l'angle en bas du dessin, on doit donc choisir le bon rapport trigonométrique.

Ici, on a le côté opposé à l'angle et le côté adjacent. On va donc utiliser tan.

Donc, tan x= opp/adj=10/34.

N'oublie pas de faire tan-1 pour trouver l'angle.

Si tu ne trouves pas ton erreur, envoie moi une photo du problème! Je vais pouvoir t'aider!

J'espère t'avoir aidé!

Lea-Kim

Tes calculs sont bons.

C'est parce que l'angle d'élévation est à partir de l'horizontale (et non de la verticale): c'est donc 90º - 16º = 74º

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-angles-de-depression-et-d-elevation-m1282

Rebonjour!

Merci de ton retour!

J'ai trouvé ton erreur. Tu ne dois pas faire diviser par 16pi mais bien soustraire 16pi.

Comme il y a une addition avec la partie contenant l'inconnu, on doit le soustraire pour l'enlever.

Ça devrait marcher!

Sinon, reviens moi!

Lea-Kim