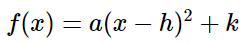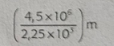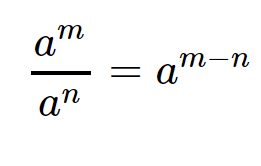Best Of

Salut!

Pour chaque fonction, tu dois trouver la règle qui a la forme suivante :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

où h et k sont les sommets de la parabole.

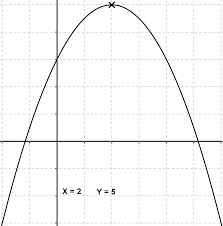
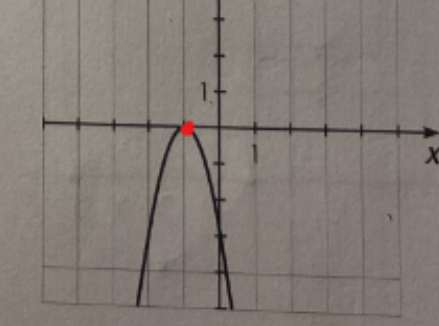
Si la parabole est ouverte vers le bas, son sommet est le point le plus en haut, comme ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

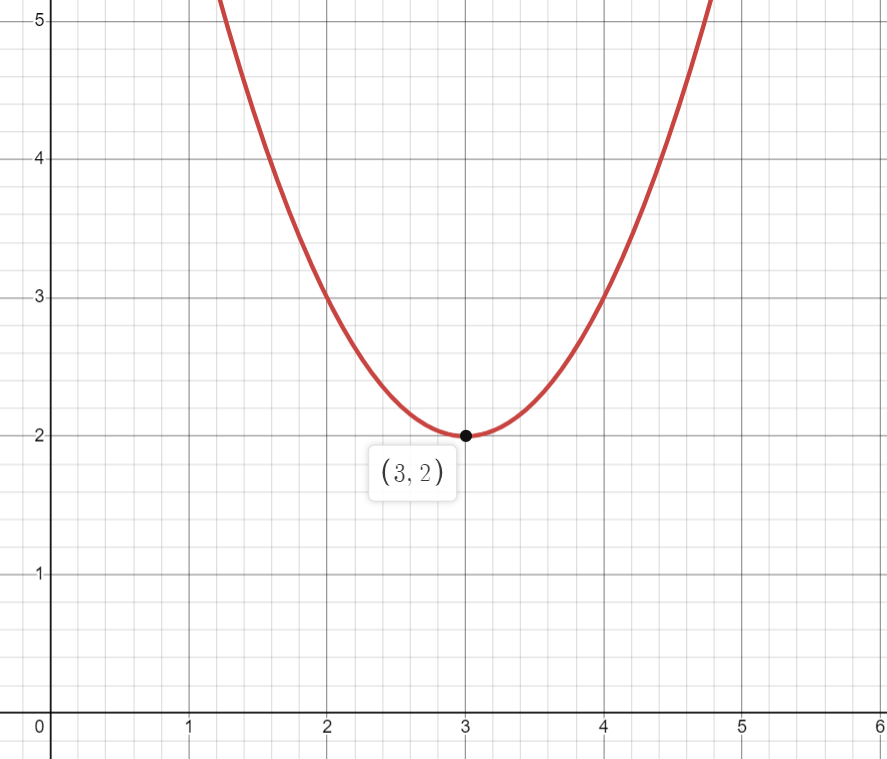
tandis que si la parabole est ouverte vers le haut, son sommet est le point le plus en bas :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, les coordonnées de ce sommet te donneront la valeur des paramètres h et k.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

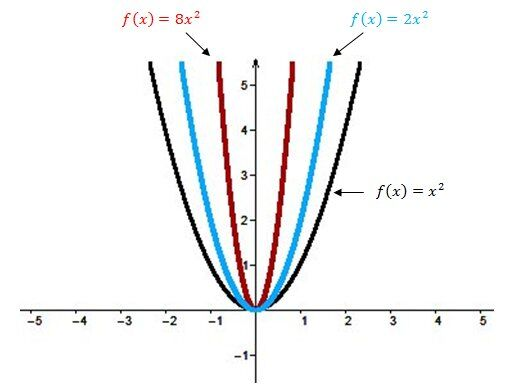
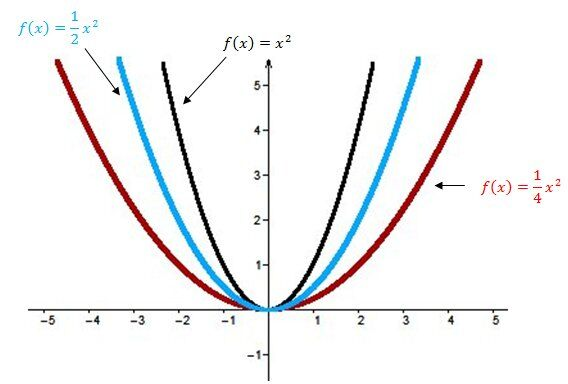
Le paramètre \(a\) influence la grandeur de l'ouverture de la parabole :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

tandis que son signe permet de déterminer si la parabole est ouverte vers le haut ou vers le bas.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

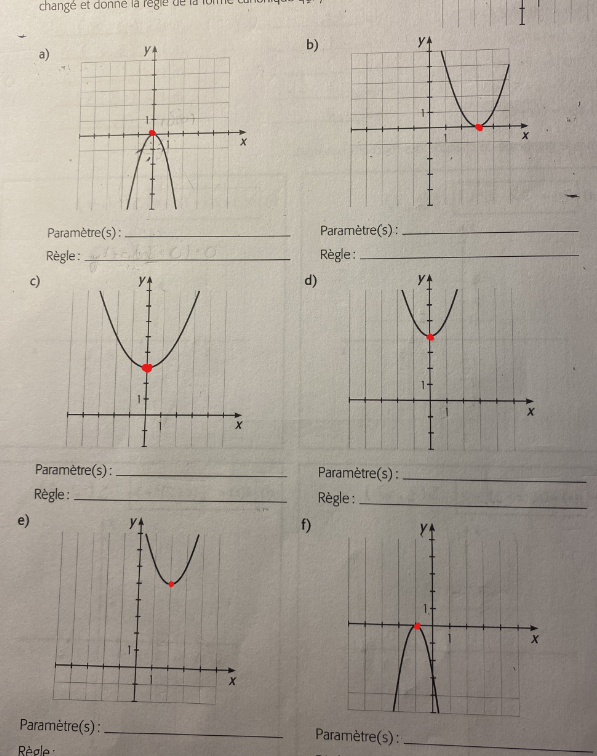
Donc, pour toutes les fonctions qui sont ouvertes vers le bas, tu sais que le paramètre a est négatif.

Pour déterminer la valeur absolue du paramètre (la valeur de a, sans prendre en compte son signe), tu peux y aller approximativement. Par exemple, pour le numéro f, l'ouverture est visiblement plus petite que celle de la fonction de base f(x)=x². Ainsi, cela veut dire que la valeur absolue de \(a\) est supérieure à 1.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici des fiches sur cette notion qui pourraient t'être utiles :

• Trouver la règle d'une fonction polynomiale de degré 2 | Secondaire | Alloprof
• Le rôle des paramètres dans une fonction polynomiale de degré 2 | Secondaire | Alloprof

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Merci pour ta question!

Il y a deux étapes principales à ce problème :

1. Simplifier les fractions
2. Approximmer à quel nombre ils sont égal.

Tout d'abord, simplifions la fraction en a). On peut diviser par 10 au numérateur et au dénominateur.

$$ \frac{50}{200} = \frac{5}{20} $$

Puisque 20 est divisible par 5, on peut aussi le diviser :

$$ \frac{5}{20} = \frac{1}{4} $$

Puis, reste à approximmer sa valeur. 1/4 est grand que 0, mais plus petit que 1/2. On peut ainsi le placer entre ces deux points.

Voilà!

Cette fiche du site d'Alloprof explique les fractions :

N'hésite pas si tu as d'autres questions!

Bonjour

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La réponse du a est 1/2 tu c`est comment je les trouver . je me suis dit que 1 présente un gros complet qui est = a 100 et je me suis dit aussi que 2 représente 200 .Donc si 200 diviser par 50 donne 4 et que le 50 représente 1/4 de 200 alors si 100 représente 1 gros complet .alors si 50 est la moitié de 100 alors ca représente 1/2. Éssaie de faire le b j`ai confiance on toi .

Bonne chance.

Bonjour! Pour cette question, tu as besoin de faire une réduction. Par exemple, 2/4 peut être réduit et devenir 1/2. Par la suite, tu dois estimer où cette fraction réduite se situe sur la bande

Tu as 8 pointes par tarte et tu as trois tartes, tu as donc au total:

3x8 = 24 pointes de tarte

si n représente le nombre de personnes alors tu auras

24/n pointes de tarte par personne

Note: porte attention aux unités cela t'aidera à éviter les erreurs: si tu avais fait n/24 tes unités seraient personnes/pointe

Salut!

Tes démarches sont excellentes, bon travail! Tu as une toute petite erreur ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici comment simplifier cette expression :

$$ \frac{4,5\times 10^6}{2,25 \times 10^5} $$

On peut commencer par séparer les puissances de 10 des facteurs :

$$ \frac{4,5}{2,25} \times \frac{10^6}{10^5} $$

On divise ensuite 4,5 par 2,25, ce qui nous donne 2 :

$$2 \times \frac{10^6}{10^5} $$

Maintenant, pour simplifier la seconde fraction, on peut utiliser la loi des exposants suivante :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

ce qui nous permet d'obtenir :

$$2 \times 10^{6-5} $$

$$2 \times 10^{1} $$

$$2 \times 10 = 20 $$

Tu dois donc refaire ton calcul de la longueur totale du parcours :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le reste de ta démarche est bon, bien joué! :)