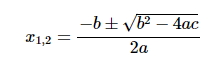Best Of
Re: Question
salut ! Un atome, c'est la plus petite unité composant la matière. Par exemple, l'azote. Un élément, est une substance pure formée de seulement une seule sorte d'atomes. Ceci veut dire qu'un élément, c'est un ensemble d'atomes. C'est un peu comme un atomes au pluriel ;))
Re: Question
Re salut!
Contente que mon explication t'ait été utile! :D
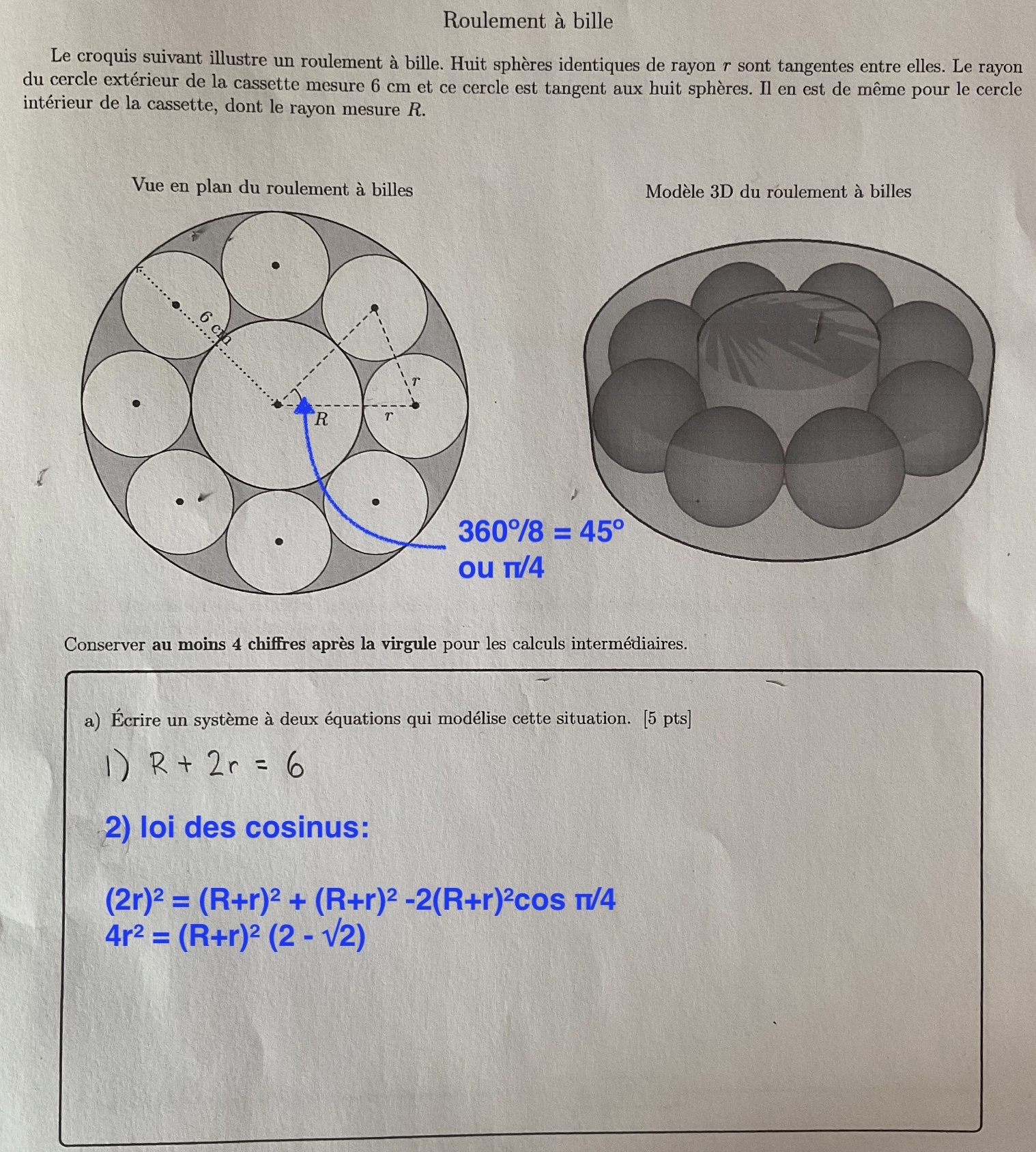
Pour trouver la valeur des variables r et R, tu dois résoudre le système d'équations que nous avons trouvé précédemment, soit :
$$ R+2r=6$$
$$4r^2=(R+r)^2(2-\sqrt{2})$$
Pour ce faire, utilisons la méthode de substitution. Nous allons commencer par isoler R dans la première équation :
$$ R+2r=6$$
$$ R+2r-2r=6-2r$$
$$ R=6-2r$$
Puis, nous allons insérer l'expression correspondante à la variable R dans la seconde équation, comme ceci :
$$4r^2=(R+r)^2(2-\sqrt{2})$$
$$4r^2=((6-2r)+r)^2(2-\sqrt{2})$$
On simplifie l'équation :
$$4r^2=(6-2r+r)^2(2-\sqrt{2})$$
$$4r^2=(6-r)^2(2-\sqrt{2})$$
$$4r^2=(6-r)^2(0,5858)$$
Nous allons maintenant développer l'expression, plus particulièrement le (6-r)² :
$$4r^2=(6-r)(6-r)(0,5858)$$
$$4r^2=(36-6r-6r+r^2)(0,5858)$$
$$4r^2=(36-12r+r^2)(0,5858)$$
$$4r^2=(36-12r+r^2)(0,5858)$$
On distribue la multiplication sur chaque terme de la parenthèse :
$$4r^2=21,088-7,029r+0,5858r^2$$
On déplace le terme du côté gauche de l'équation :
$$4r^2-4r^2=21,088-7,029r+0,5858r^2-4r^2$$
$$0=21,088-7,029r+(0,5858-4)r^2$$
$$0=21,088-7,029r-3,414r^2$$
On peut réordonner nos termes pour que l'expression soit plus lisible :
$$0=-3,414r^2-7,029r+21,088$$
Tu peux ensuite utiliser la formule quadratique pour résoudre cette équation.
$$ x_{1,2} = \frac{-(-7,029) ± \sqrt{(-7,029)^2-4(-3,414)(21,088)}}{2(-3,414)} $$
Je te laisse faire le dernier calcul. Voici une fiche qui pourrait t'être utile : La résolution de systèmes d'équations linéaires | Secondaire | Alloprof
Si tu as d'autres questions, on est là! :)
Re: Question
Salut ElfeGamma2582!
Merci d'avoir utilisé la zone d'entraide pour répondre à tes questions.
Tout d'abord, un mouvement unidirectionnel ne se fait que dans une seule direction.
Tandis que un mouvement se fesant dans les deux sens comme un mouvement de va-et-vient, se nomme un mouvement bidirectionnel . Bref, voici un lien pour mieux comprendre:
J'espère que cela répond à ta question.
Bonne étude!
PerleCharismatique3289 :)
Question
Bonjour
J'aurais une question spécialement pour Katia K mais les autres vous pouvez répondre aussi!
Quand Katia K m'as répondue a cette question( voici le lien: https://www.alloprof.qc.ca/zonedentraide/discussion/55682/question/p1#Comment_73497) Je n'ai pas compris le mot «côtés».
Voici la vraie feuille: https://www.alloprof.qc.ca/zonedentraide/discussion/55682/question/p1#Comment_73497
Voici la feuille que je me questionne le mot «côtés»:
(Je suis sacrément désolé du barbouillage inapproprié)
Zhilan
Re: Question
@@
Tu as eu une réponse plus complète de Fer dans un message précédent.
.
Re: Question
Salut!
La première équation que tu as trouvée est bonne, bien joué! :D
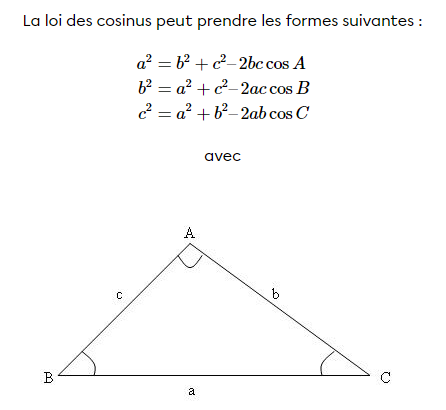
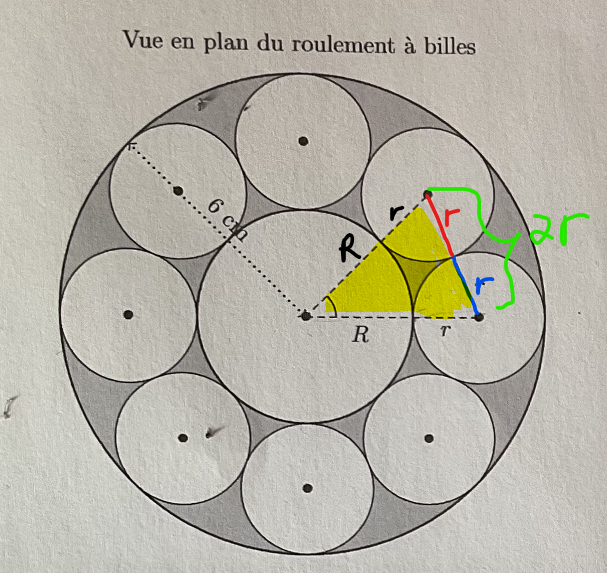
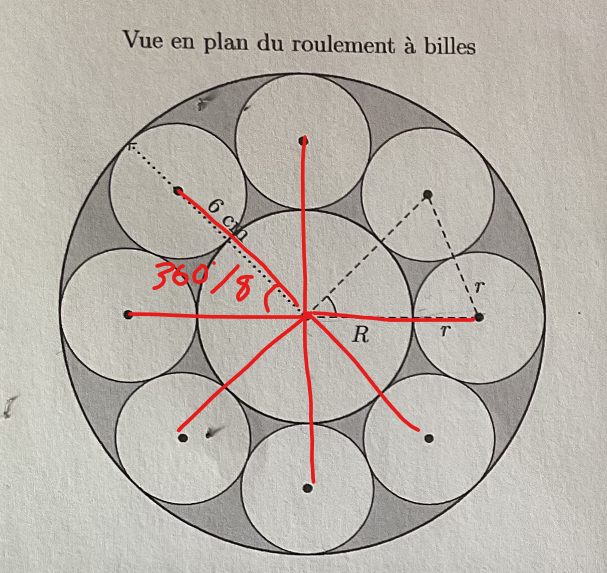
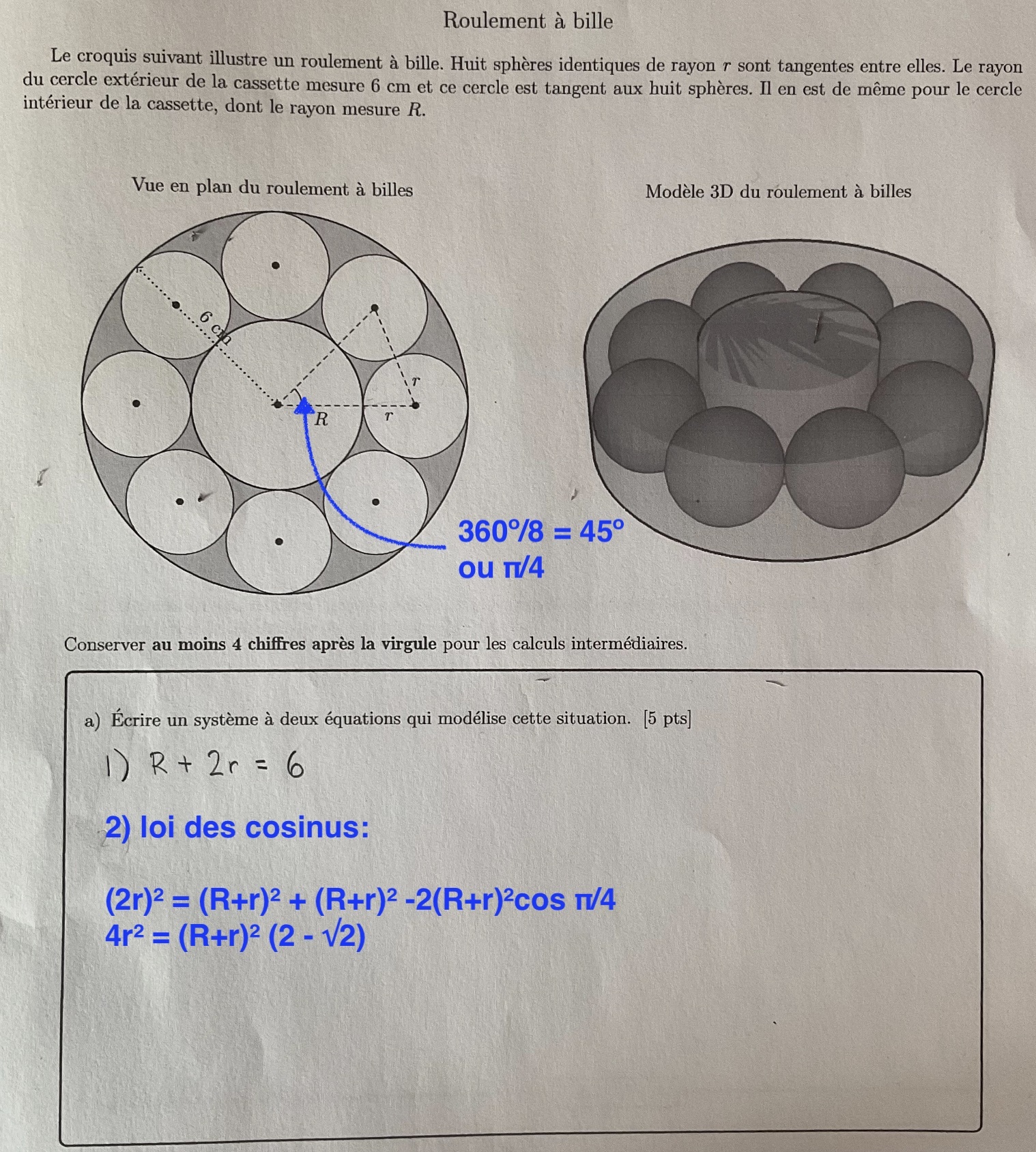
Pour trouver la seconde, tu dois utiliser la loi des cosinus.
sur le triangle suivant :
On sait que le rayon des petits cercles est identique, ce qui nous permet de déduire qu'un des côtés du triangle jaune mesure \(2r\) (r+r).
En appliquant la loi des cosinus sur le triangle, on a alors l'équation :
$$ (2r)^2 = (R+r)^2 + (R+r)^2 - 2 (R+r) (R+r) cosθ$$
que l'on peut simplifier pour avoir :
$$ (2r)^2 = 2(R+r)^2 - 2 (R+r)^2 cosθ$$
$$ 4r^2 = 2(R+r)^2 - 2 (R+r)^2 cosθ$$
On peut factoriser (R+r)², ce qui nous donne :
$$ 4r^2 = (R+r)^2 (2- 2cosθ)$$
Puisqu'on souhaite avoir un système avec 2 inconnus seulement, soit R et r, il faut alors trouver la valeur de θ, soit l'angle en radians (car on utilise la loi des cosinus = on doit être en radians et non en degrés) dans le triangle.
Pour trouver cet angle, nous n'avons qu'à diviser 360° par 8, puisqu'il y a 8 cercles.
On trouve alors que l'angle dans le triangle est de 45 degrés, ce qui équivaut à π/4 radians.
On aurait également pu diviser 2π (car 2π radians = 360 degrés = un tour complet dans le cercle trigonométrique) par 8, ce qui nous donnerait directement l'angle en radians, soit π/4 radians.
On vient finalement insérer cet angle dans notre équation :
$$ 4r^2 = (R+r)^2 (2- 2cos\frac{\pi}{4})$$
Et on simplifie :
$$ 4r^2 = (R+r)^2 (2- 2\frac{\sqrt{2}}{2})$$
$$ 4r^2 = (R+r)^2 (2- \sqrt{2})$$
On a ainsi trouvé notre seconde équation du système d'équations! :D
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Bonjour CoccinelleHumoristique8760!
Merci pour ta question!
Dans ce problème il ya question de variable et d'algèbre. On nous dit Annabelle a fait 4 descentes intérmédiaires de plus que le double de descentes extrêmes. Le nombre de descentes extrêmes est inconnu donc nous pouvons le remplacer par n'importe quel variable, utilisons ''x'' par exemple. L'équation serait 2x+4 ou 4+2x.
Ensuite, on nous indique que le rapport entre les pistes intermédiaire et extrême est de 8:3 donc nous devons mettre l'équation en forme de proportion donc 8x(4 + 2x) et 3x(4 + 2x) soit 32 + 16x : 12 + 6x.
Si tu veux en apprendre d'avantage sur les proportions voici une fiche qui peut t'aider :
J'espère que celà répond a ta question et bonne continuation!
GalaxieAdmirable6894
Re: Question
Bonsoir CoccinelleHumoristique8760,
Merci de poser des questions sur la zone d'entraide!
Premièrement, dans ton problème, le produit croisé est nécessaire, car tu dois trouver la variable `x` ; nombre de descentes dans une piste de niveau extrême.
Deuxièmement, je te recommande de regarder ces liens:
https://www.alloprof.qc.ca/en/students/vl/mathematics/proportions-m1547
N'hésite pas de poser d'autres questions!
Re: Question
Salut!
On te dit qu'Annabelle fait 4 descentes dans une piste de niveau intermédiaire de plus que le double du nombre de descentes dans une piste de niveau extrême. On peut traduire cet énoncé en l'équation suivante :
Nombre de descentes intermédiaire = 2 × nombre de descentes expert + 4
On nous dit également que le rapport entre le nombre de descentes dans des pistes de niveau intermédiaire et expert est de 8 : 3. En d'autres mots, on a le rapport :
$$\frac{nombre~ de ~descentes~ intermédiaire}{ nombre ~de~ descentes~ expert} = \frac{8}{3}$$
On peut réécrire le rapport en insérant notre première équation :
$$\frac{2\times nombre~ de ~descentes~expert+ 4}{nombre~de~descentes~expert} = \frac{8}{3}$$
Si on remplace la variable "nombre de descentes dans une piste de niveau expert" par x, on a :
$$\frac{2x+ 4}{x} = \frac{8}{3}$$
Il ne reste plus qu'à résoudre cette équation pour trouver x. Tu pourras finalement calculer le nombre de descentes sur une piste de niveau intermédiaire à l'aide de x.
Voici une fiche qui pourrait t'être utile : Les méthodes générales de résolution d'équations | Secondaire | Alloprof
Je te laisse essayer avec ces indices. Si tu as d'autres questions, n'hésite pas à nous réécrire! :)