Best Of

Pour l'examen de ministère de math de secondaire 4, en statistiques, est-ce qu'il faut savoir les deux méthodes (Mayer et médiane-médiane) ou juste l'une d'entre elles est correct?

Ta fonction g(x) existe de y=0 jusqu'à son sommet, c'est donc son image. Ça veut dire que si tu trouves sa règle, le K sous forme canonique sera ton maximum, donc l'image est [0, K]. Pour y parvenir, trouve les points Xa et Xb pour trouver la règle de g(x) sous forme factorisée et ensuite la convertir en canonique. Pour Xa, tu devras trouver le 2e zéro de la fonction f(x) dont tu possèdes déjà la règle car c'est à cet endroit que g(x) et f(x) se croisent. Pour Xb, tu possèdes le sommet de h(x) et un point, tu peux donc trouver sa règle. Avec cette règle de h(x), trouve le premier zéro de h(x), qui est le point Xb où g(x) et h(x) se croisent. Maintenant que tu as les deux zéros de la fonction g(x) et que tu possèdes déjà le point F(28,24) dans cette fonction, isole le "A" dans la règle de forme factorisée, ce qui te donnera la règle de g(x) sous forme g(x)=A(x-z1)(x-z2) où z1 et z2 sont tes zéros (xa et xb). Transforme la ensuite sous forme canonique g(x)=A(x-h)2+K et le K sous cette forme sera ton maximum, ton image étant f(x) E [0, K]. Republie quelque chose si tu as d'autres questions chef

oui, étudier avec un crayon et des yeux

Oui moi je me coucherai tôt mangerai bien et bien révisé

oui tu dois te faire confience te concentrer prendre le temp de te relire regarder si tes phrases sont biens formées

Dors bien prend une bonne collation qui aide a la concentration comme des amandes ou des carottes et si tu es stressé apporte de la gum et aussi stresse pas c'est vraiment facile

pour résoudre cette inéquation, il faut premièrement la transformer à une équation:

7(x+25)(x-10) = 0

on divise les deux côtés par 7, et le 7 qu'est à gauche sera annulé:

(x+25)(x-10) = 0/7

(x+25)(x-10) = 0

alors: x1 + 25 = 0 et x2 - 10 = 0

x1 = -25 et x2 = 10

Puis, on va prendre un nombre entre les deux nombres (par exemple, 0) et on va remplacer le x par 0:

7(x+25)(x-10) > 0

7(0+25)(0-10) > 0

7*25*(-10) > 0

-1750 > 0

Cette expression n'est pas vraie, alors, on prendra les chiffres plus petits que -25 et les chiffres plus grands que 10.

En plus, le symbole > est strictement supérieur, les chiffres -25 et 10 seront alors exclus:

x ∈ ]-∞, -25[ U ]10, ∞+[

Notez bien que les infinis sont toujours exclus.

J'espère que ça t'a aidé, et bonne chance pour l'examen de ministère!

Salut!

Pour résoudre cette équation, tu dois commencer par la transformer en équation :

$$7(x+25)(x-10)=0$$

Tu peux ensuite la résoudre comme à l'habitude :

$$\frac{7(x+25)(x-10)}{7}=\frac{0}{7}$$

$$(x+25)(x-10)=0$$

On divise en deux équations :

$$(x+25)=0$$

$$x=-25$$

et

$$(x-10)=0$$

$$x=10$$

Nos solutions sont donc x=10 et x=-25.

Tu pourrais également résoudre cette équation en la mettant sous forme générale puis en utilisant la formule quadratique.

Voici une fiche qui pourrait t'aider pour passer de la forme factorisée à la forme générale : Les formes d'écriture de la fonction polynomiale de degré 2 | Secondaire | Alloprof

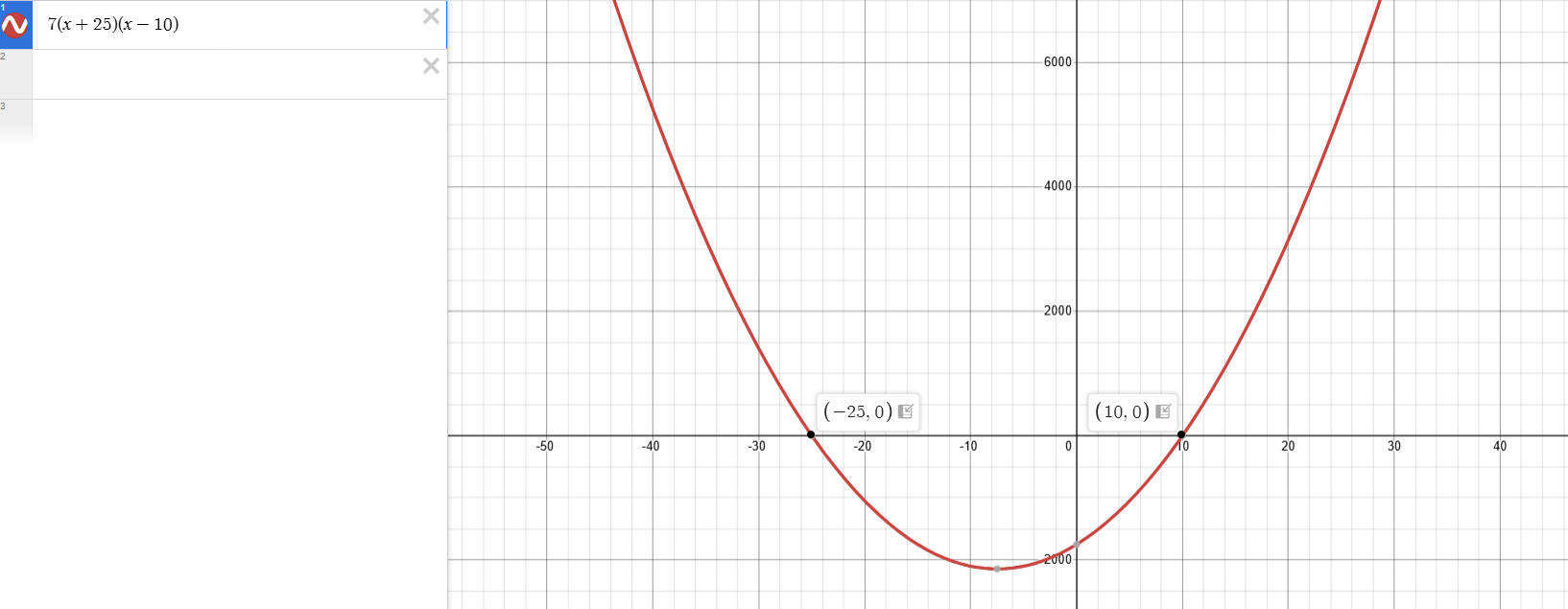
Maintenant, tu dois tracer une esquisse de ta parabole. Tu sais que les zéros de la parabole 7(x+25)(x-10) sont x=10 et x=-25. De plus, puisque le paramètre a (qui est 7) est positif, alors la parabole est ouverte vers le haut. Cela nous donne ce graphique (tu n'es pas obligé de le faire à l'échelle. En fait tu ne devrais pas, sinon ça serait long en examen. Tu dois simplement connaitre l'allure générale pour pouvoir identifier ensuite l'intervalle recherché) :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

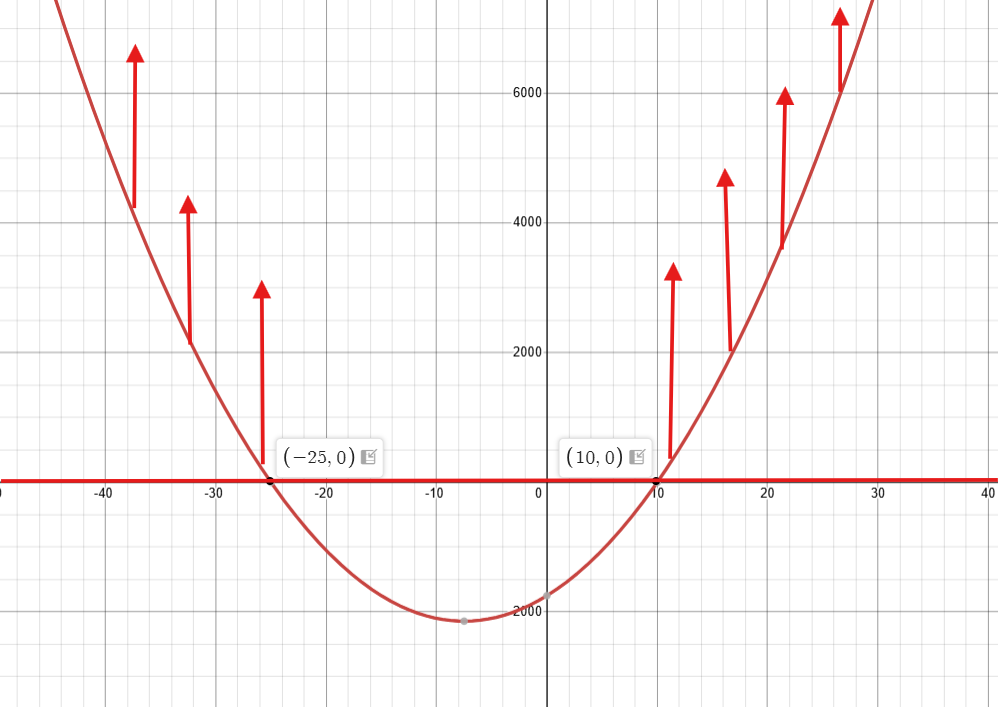
On cherche l'intervalle pour lequel la fonction est supérieure à y=0.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

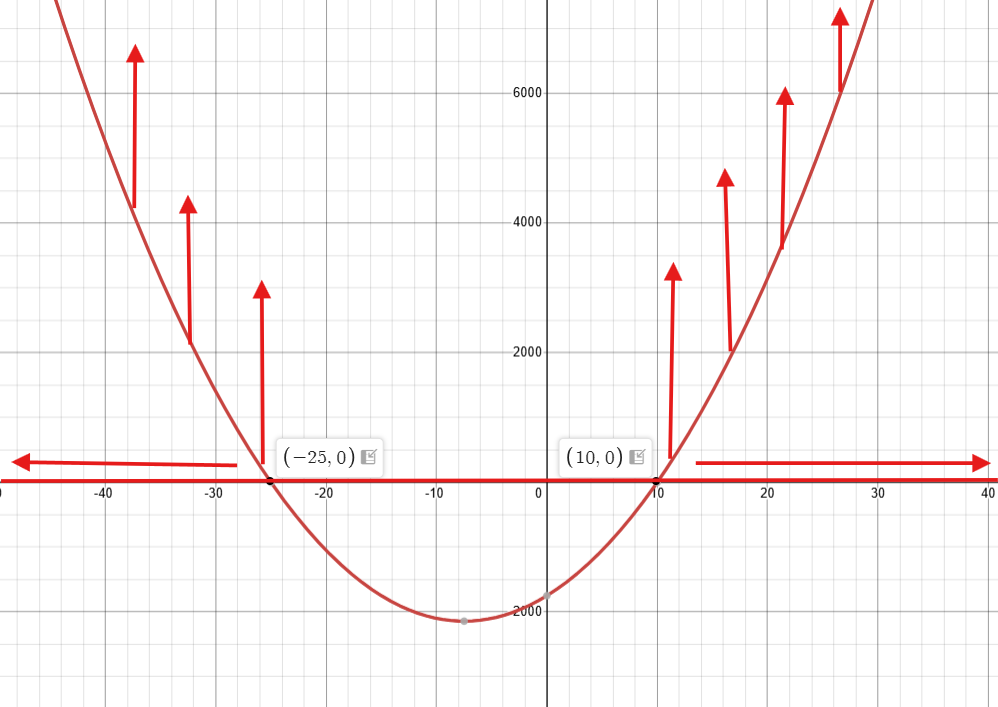
On voit donc qu'on est supérieure à y=0 de x=-∞ à x=-25, et de x=10 à x=∞.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La réponse de l'inéquation est donc : ]-∞, -25[ U ]10, ∞[.

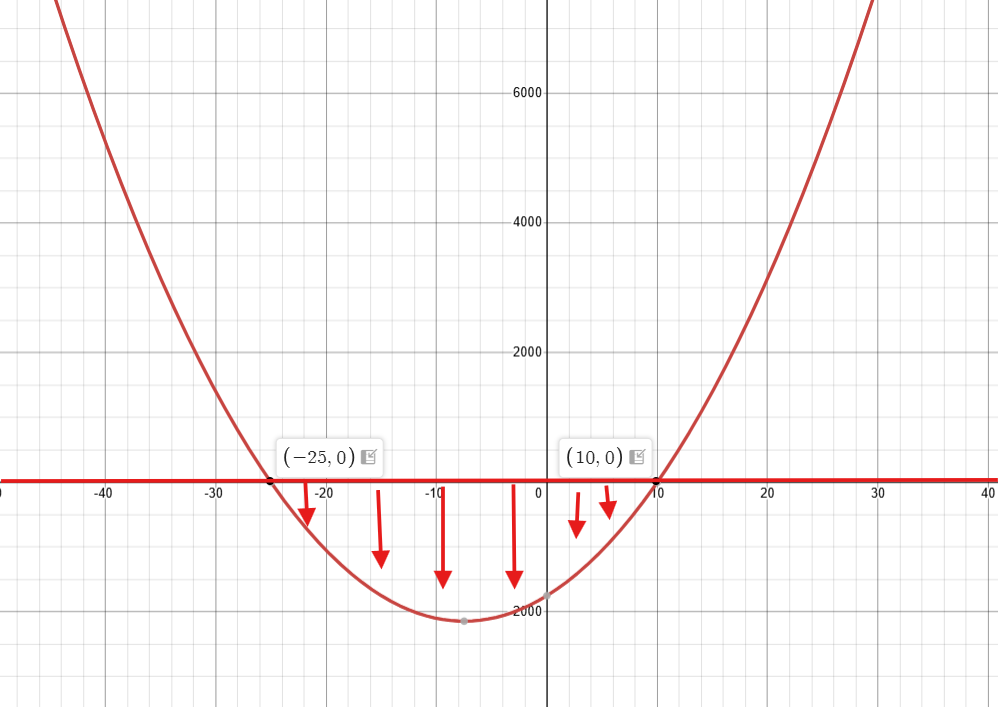
Si tu avais eu le signe inverse :

$$7(x+25)(x-10)<0$$

Alors on chercherait l'intervalle où la fonction est inférieure à y=0.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc, la réponse aurait été ]-25, 10[.

J'espère que c'est plus clair pour toi! :)