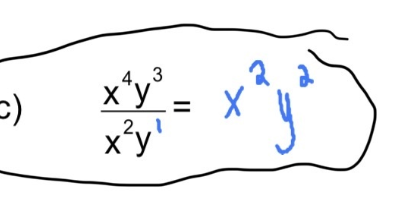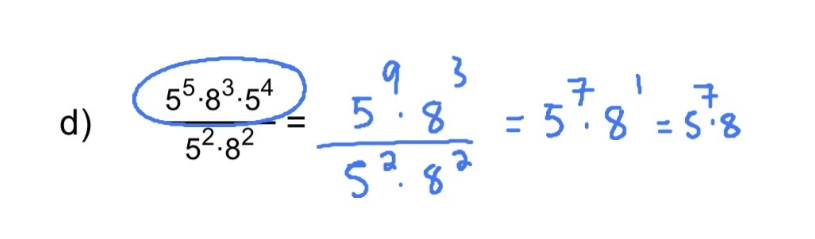Best Of
Re: Question
Bonjour OrioleOrange7335! :D
Merci pour ta question! :D
Selon Bohr, ce qu’il faut comprendre, c’est qu’un électron ne tombe pas sur son noyau parce qu’il possède exactement la bonne quantité d’énergie pour rester sur sa couche électronique. On peut comparer ça à une planète qui garde son orbite grâce à sa vitesse : l’analogie fonctionne assez bien ici!
Par contre, il y a une différence importante : un électron peut changer de couche électronique en variant son niveau d’énergie. S’il absorbe ou libère une quantité d’énergie bien précise (sous forme de lumière), il pourra passer d’une couche à une autre… chose qu’une planète ne peut pas faire!
J'espère que j'ai répondu à ta question! Si tu as d'autres questions, n'hésite pas à revenir nous voir! :)
Passe une belle journée! :D
Re: Question
Bonjour RubisIntergalactique3026! :D
Merci pour ta question! :D
Un vecteur vitesse est un vecteur qui décrit à la fois la rapidité et la direction d’un mouvement. Par exemple, on peut dire qu’un objet se déplace à 12 km/h vers le nord : 12 km/h représente la norme (ou grandeur) et « vers le nord » indique l’orientation. Si on précise aussi un angle, comme « à 30° par rapport à l’horizontale », cela donne encore plus de détails sur la direction.
Quand on te demande une réponse vectorielle, tu dois donc toujours donner la norme du vecteur (sa grandeur en unités de vitesse, comme km/h ou m/s) et son orientation (la direction ou l’angle par rapport à une référence, par exemple l’axe horizontal ou un point cardinal). Cela permet de décrire complètement la vitesse. Si on ne peut pas trouver d'angle (par exemple, on ne peut pas déterminer l'angle du nombre de raisin ;)) , la réponse est un scalaire! :)
J'espère avoir répondu à ta question! Si tu as d'autres questions, n'hésite pas à revenir nous voir! :D
Passe une bonne journée! :D
Re: Question
Salut!
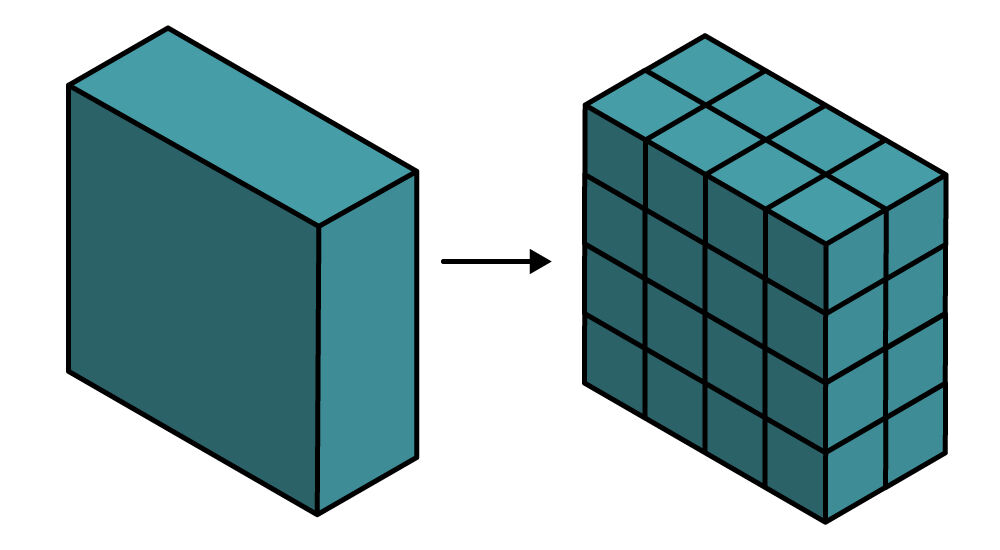
Le volume correspond à la mesure de l'espace occupé par un solide.
Par exemple, le volume d’une boite correspond à l’espace qu’elle occupe.
Pour connaitre le volume d'un solide, on peut placer des cubes-unités (qui sont tous de la même grosseur) à l'intérieur du solide. Le nombre de cubes-unités utilisés pour remplir l'espace occupé par le solide sera la mesure de notre volume.
Par exemple, le volume de ce solide est de 32 cubes-unités, parce que 32 petits cubes peuvent être placés à l’intérieur du solide pour remplir entièrement l’espace qu’il occupe.
Voici une fiche qui pourrait t'être utile : Calculer le volume | Primaire | Primaire | Alloprof
N'hésite surtout pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Salut!
Le préfixe « post » signifie « après ». Donc, postsecondaire signifie « après le secondaire ».
Les personnes ayant terminé leurs études au secondaire peuvent donc choisir ce niveau lorsqu'ils nous posent des questions sur la Zone d'entraide!
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Salut!
On est là pour t'aider à mieux comprendre! :D
Donc, pour le numéro c) :
On a appliqué la loi des exposants suivante :
On a donc eu ceci :
$$ \frac{x^4y^3}{x^2y}$$
$$=x^{4-2}y^{3-1}$$
$$=x^{2}y^{2}$$
C'est tout! :)
Pour le d) :
On a appliqué cette loi :
Ce qui fait en sorte que l'on peut simplifier le numérateur en fusionnant \(5^5\) et \(5^4\) :
$$\frac{5^5 \times 8^3 \times 5^4}{5^2 \times 8^2}$$
$$=\frac{5^{5+4} \times 8^3}{5^2 \times 8^2}$$
$$=\frac{5^9 \times 8^3}{5^2 \times 8^2}$$
On peut ensuite utiliser la loi du quotient (celle du numéro c) pour simplifier davantage l'expression.
$$=5^{9-2} \times 8^{3-2}$$
$$=5^{7} \times 8^{1}$$
Voilà! J'espère que c'est plus clair pour toi! :)
Re: Question
Salut !
Merci d'avoir posé ta question.
Ces fiches pourront certainement t'aider à trouver les autres :
N'hésite pas à repasser si tu as d'autres questions. :)
Angélique
Re: Question
Salut!
Oui, nous en avons d'autres! :)
Nous avons entre autres Magimot, Spellers, Grimoire, Allo Monde ou encore Gommophone.
Tu peux retrouver tous nos jeux juste ici : Jeux et applications | Alloprof
Bon jeu! :)