Best Of

Bonjour, GalaxieCocasse8582!

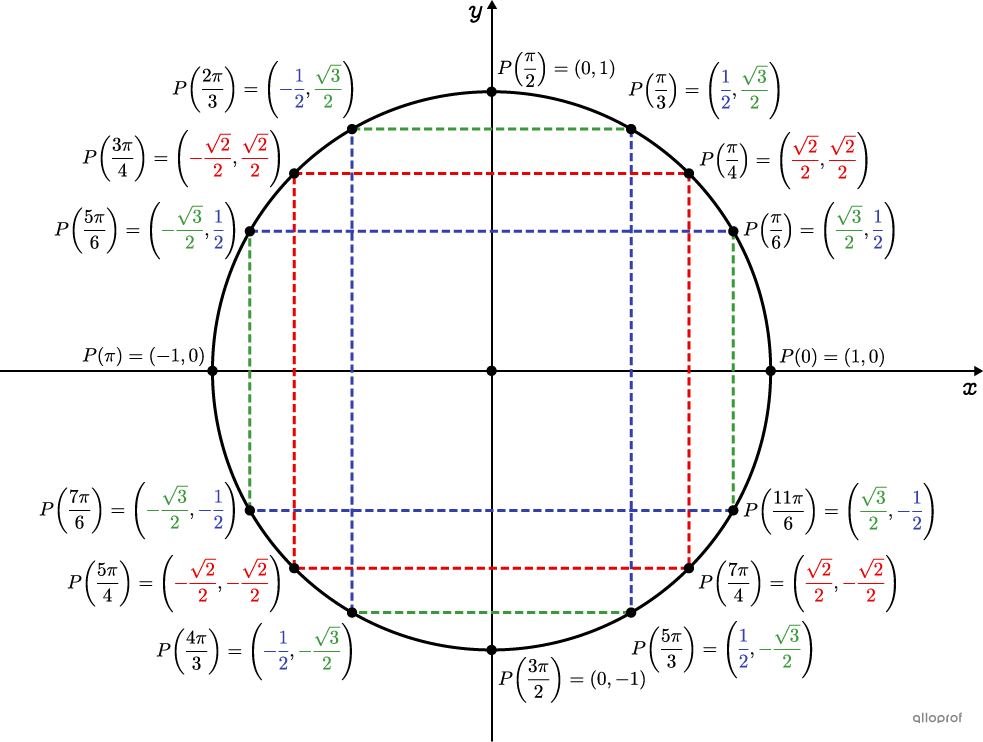
La première étape est en effet de déterminer quelle combinaison d’angles remarquables permet d’obtenir θ.

La valeur \( \dfrac{17\pi}{12} \) n'étant pas un angle remarquable, on doit la décomposer en une somme ou en une différence d'angles remarquables.

Dans le cercle trigonométrique, les angles sont sur des dénominateurs 1, 2, 3, 4 et 6.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Nous voulons des dénominateurs spécifiques, donc sépare le nombre en deux autres qui sont divisibles par certains nommés précédemment. Tu as plusieurs options.

Par exemple, 17=15+2. Donc, \(\dfrac{17\pi}{12} = \dfrac{15\pi}{12} + \dfrac{2\pi}{12}\).

Tu peux aussi donner une soustraction. Le nombre 17, c'est aussi 21-4. Ainsi, \(\dfrac{17\pi}{12} = \dfrac{21\pi}{12} - \dfrac{4\pi}{12}\).

Réduis les fractions et tu verras que chacune est un angle remarquable.

La deuxième étape est de choisir la bonne identité trigonométrique, puis la troisième de déterminer la valeur de l'expression.

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-identites-trigonometriques-m1357

N'hésite pas à poser d'autres questions!

Je ne comprends pas comment m'y prendre:

Soient les vecteurs 

u, v et w tels que 

v=4u

 w =−2u

 Lesquelles des affirmations suivantes sont vraies ?

Les vecteurs u et v sont colinéaires.

Les vecteurs u et w sont orthogonaux.

Les vecteurs v et w sont opposés.

Les vecteurs u et w ont la même direction.

La norme du vecteur u est le quadruple de la norme du vecteur v.

La norme du vecteur v est le double de la norme du vecteur w

je vais allez en secondaire 3 , mais J'ai un défauts ces que je suis extrêmes nul en problème . Avais vous une technique pour devenir meilleur .

Comment distingué La traduction d'un énoncé en équation entre:

2.(x + 5) et

2.x+ 5

Merci

Comment savoir vers où pointe le signe dans une inéquation valeur absolue? Par exemple, 2|x+3|+16>30 me donne les inéquations x+3>7 et x+3<-7. Pourquoi les signes pointes dans des directions differentes? Quand les signes devrait-il pointer dans le meme sens vs le sens opposé?

Salut!

Pour résoudre une équation contenant une valeur absolue, tu dois d'abord transformer l'inéquation en inéquation.

Voici un résumé des étapes à suivre :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Regardons comment résoudre l'inéquation :

$$2|x+3|+16>30$$

On commence par remplacer le symbole d'inégalité par un symbole d'égalité :

$$2|x+3|+16=30$$

On élimine la constante 16 :

$$2|x+3|+16-16=30-16$$

$$2|x+3|=14$$

On élimine le facteur 2 :

$$\frac{2|x+3|}{2}=\frac{14}{2}$$

$$|x+3|=7$$

On divise maintenant l'équation en deux en appliquant la définition d'une valeur absolue :

$$x+3=7$$

et

$$x+3=-7$$

Et on résout chacune équation :

$$x_{1}+3=7$$

$$x_{1}=7-3=4$$

et :

$$x_{2}+3=-7$$

$$x_{2}=-7-3=-10$$

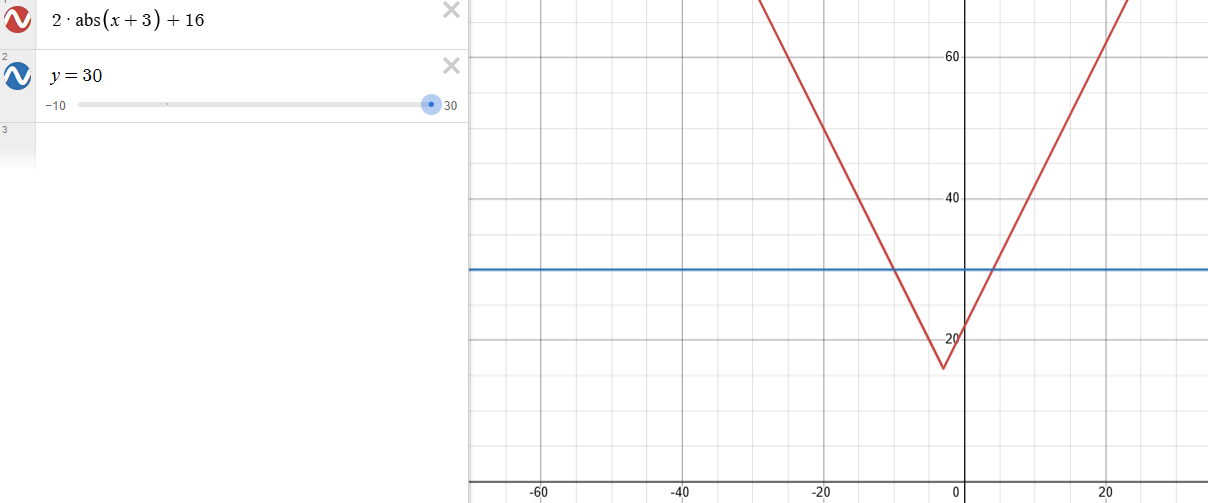
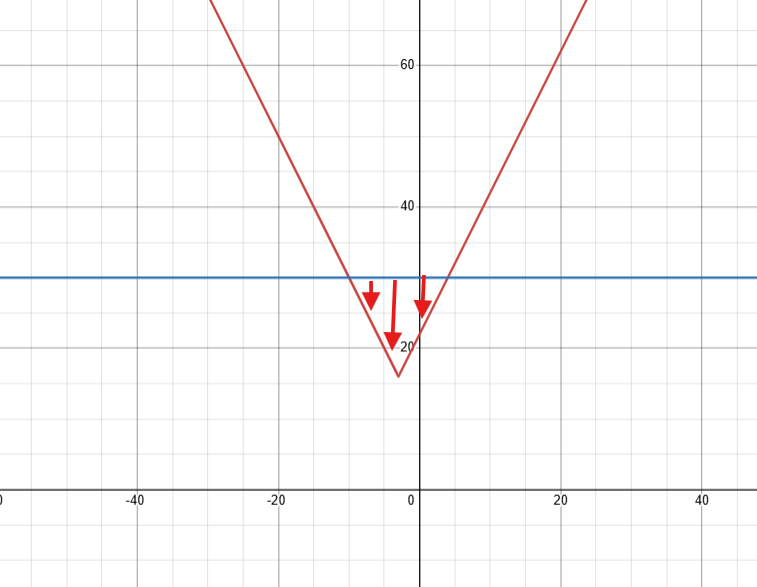
Ensuite, pour déterminer l'ensemble-solution, on se fait un petit croquis de la fonction :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Puisque le paramètre a est positif (a=2), alors la fonction est ouverte vers le haut. C'est surtout ça qu'il faut déterminer et illustrer dans notre croquis. Consulte la fiche suivante au besoin : Le rôle des paramètres dans une fonction valeur absolue | Alloprof

On sait aussi que les intersections entre la fonction valeur absolue (en rouge) et la droite y=30 (en bleu) sont x=-10 et x=4 (les solutions trouvées précédemment).

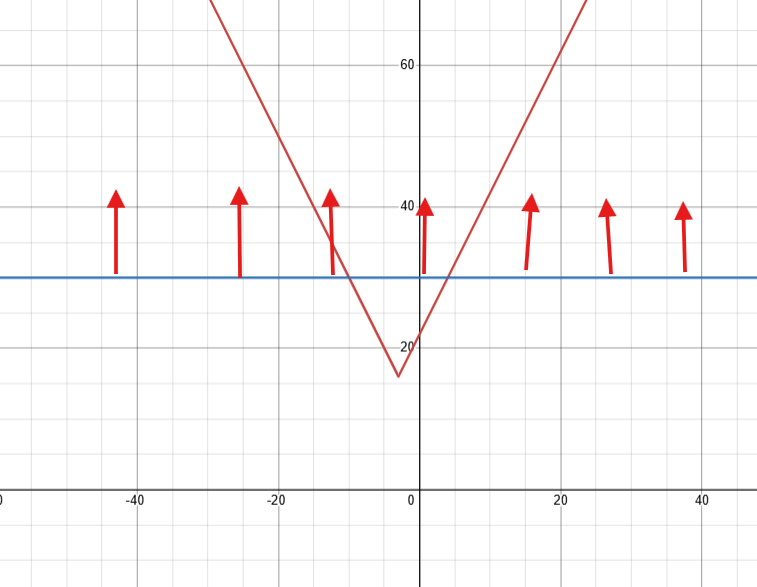
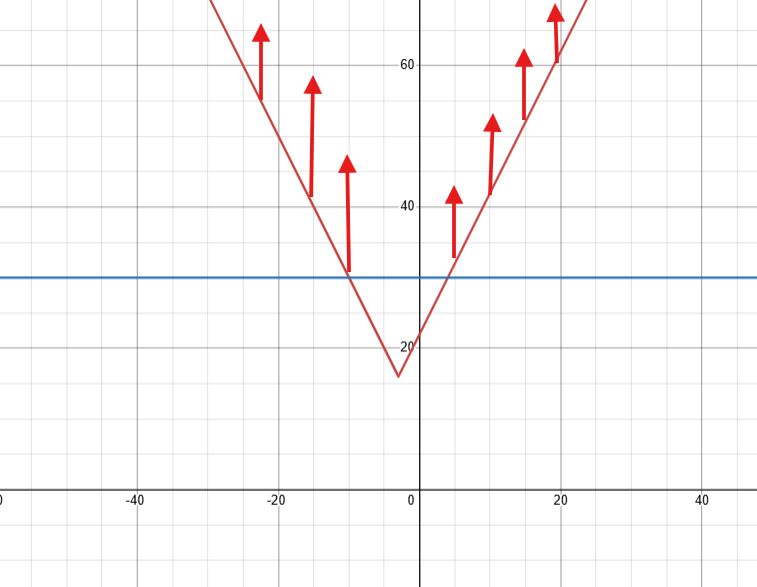
On sait aussi qu'on veut être supérieur à y=30 (2|x+3|+16>30).

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La fonction est supérieure à y=30 de x=-∞ à x=-7 et de x=4 à x=∞.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc, la réponse finale est ]-∞, -7[ U ]4, ∞[, ou encore x<-7 et x>4.

Si l'inéquation était plutôt 2|x+3|+16<30, alors la réponse serait x<4 et x>-7, ou encore ]-7, 4[.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici une fiche qui présente d'autres exemples de résolution d'inéquations contenant une valeur absolue, cela t'aidera à mieux comprendre : Résoudre une équation ou une inéquation contenant une valeur absolue | Secondaire | Alloprof

Voilà! J'espère que c'est plus clair pour toi! N'hésite pas à nous réécrire si tu as d'autres questions! 😁