Best Of
Re: Question
Salut AraSigma6635 !
Merci de faire appel à la zone d'entraide. :)
Le groupe adverbial (GAdv), aussi appelé groupe de l’adverbe, est un groupe de mots dont le noyau est un adverbe.
Pour repérer un groupe adverbial, trouve un adverbe dans la phrase. Il est souvent accompagné d'un ou plusieurs mots qui modifient ou complètent son sens.
Voici notre fiche sur le groupe adverbial si tu veux en savoir plus:
Voici notre fiche sur la fonction du groupe adverbial :
N'hésite pas à repasser si tu as d'autres questions. :)
Angélique
Re: Question
Bonjour PerroquetAdmirable,
Merci pour ta question!
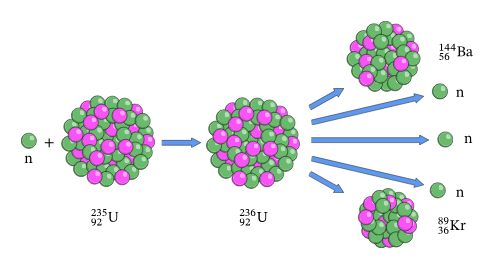
Il est possible de "séparer" un élément. C'est par exemple le cas lorsque l'on fait de la fission nucléaire. C'est le phénomène utilisé dans les centrales nucléaires et les bombes atomiques.
Par exemple, sur cet image, en provoquant la collision à haute vitesse de deux atomes d'uranium (un élément), on obtient un atome de Krypton (un autre élément) et de Baryum (un autre élément).
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Salut!
Les informations que tu as trouvées sont bonnes, c'est un bon début :)
Maintenant, tu peux commencer par trouver la règle de la fonction f avec les informations connues (sous forme canonique ou sous forme factorisée, c'est ton choix).
Une fois que tu connais la règle de la fonction f, tu peux calculer sa valeur initiale, c'est-à-dire la valeur de y lorsque x=0.
Cette valeur initiale est la même que celle de la fonction g (voir énoncé souligné en vert). Donc, avec la valeur initiale de g, le point (6,6) et la valeur du paramètre k, tu pourras trouver l'équation de la fonction g.
Avec la règle de g, tu pourras calculer les zéros :D
Je te laisse essayer avec ces indices. Si tu as d'autres questions, n'hésite pas à nous réécrire! 🙂
Re: Question
Je te conseil de faire de l'étude 30 min tout les jour. Comme ça tu fais tes études régulièrement et tu as aussi du temps pour tes autres activités.
SaumonTurbo3944😁
Question
Bonsoir :)
Je devrais faire quelques suggestions pour la création de sa murale.
Pourriez-vous s.v.p m'aider ?
Merci de votre aide 😊!
Re: Question
Bonjour AlligatorDelta,
Merci pour ta question!
Un angle d'incidence plus petit que l'angle critique entraînera une réfraction de la lumière (donc elle sortira du milieu).
Un angle d'incidence plus grand que l'angle critique entraînera plutôt une réflexion totale interne de la lumière (elle restera dans le milieu).
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Bonjour,
Je ne te conseille pas de te fier sur ChatGPT là-dessus. Tu devrais reviser tout ce que tu as appris au long de l'année.
Voici notre répertoire de révision pour les maths CST, SN, TS de secondaire 4 :
Si tu as besoin d'aide avec certaines notions, n'hésite pas à venir poser tes questions !
Bonne journée :)
Re: Question
Salut RubisAdorable3326 !
Merci d'avoir posé ta question. :)
Les résultats obtenus aux épreuves ministérielles seront transmis aux élèves par la poste.
Tu peux en savoir plus juste ici :
N'hésite pas à repasser nous voir si tu as d'autres questions. :)
Angélique
Re: Question
Bonjour SaumonMagnifique,
Merci pour ta question!
Pour ta première question, oui, toute réaction dont l'oxygène fait partie des réactifs sont des réactions d'oxygénation par définition.
Pour plus d'informations:
Pour ta deuxième question, l'énergie chimique est l'énergie qui est "stockée" dans les liaisons entre les atomes qui forment les molécules de différentes substances. Ce n'est donc pas faux de le visualiser comme étant une substance dans laquelle "il ne se passe rien" actuellement, mais dans laquelle il peut se passer quelque chose plus tard.
Par contre, ton truc pourrait te jouer des tours, puisqu'une substance où "il ne se passe rien" en apparence ne représente pas nécessairement de l'énergie chimique. Par exemple, l'énergie contenue dans l'uranium est considérée de l'énergie nucléaire, et l'énergie du Soleil est considérée de l'énergie solaire.
Tu peux plutôt te demander s'il y a une autre forme d'énergie en jeu dans la substance/l'objet. Si la seule forme d'énergie en jeu semble être l'énergie potentielle que contiennent ses molécules, c'est qu'il s'agit d'énergie chimique.
Pour plus d'informations:
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Bonjour RomanticWolf2696,
Merci pour ta question!
Je te comprends très bien! Lorsque les examens finaux arrivent, il faut étudier plusieurs matières en même temps, ce qui donne une bonne charge d'étude. C'est pour cette raison qu'il faut être organisé et bien structuré!
Je trouve ça super que tu veuilles avoir des trucs pour étudier! Ça montre un bel engagement!
Ci-dessous, il y a une réponse très détaillée qu'une de mes collègues a donnée par le passé. Tu y trouveras plusieurs trucs et plusieurs ressources qui pourront t'aider à réviser pour tes examens. La voici :
J'espère t'avoir aidé. Continue ton bon travail et n'hésite pas si tu as d'autres questions!
Zachary T. :)