Best Of
Re: Question
Salut GalaxieTurquoise2162!
Je vais très bien et j'espère qu'il en est de même pour toi. 😄
Merci pour ta question. 🤩
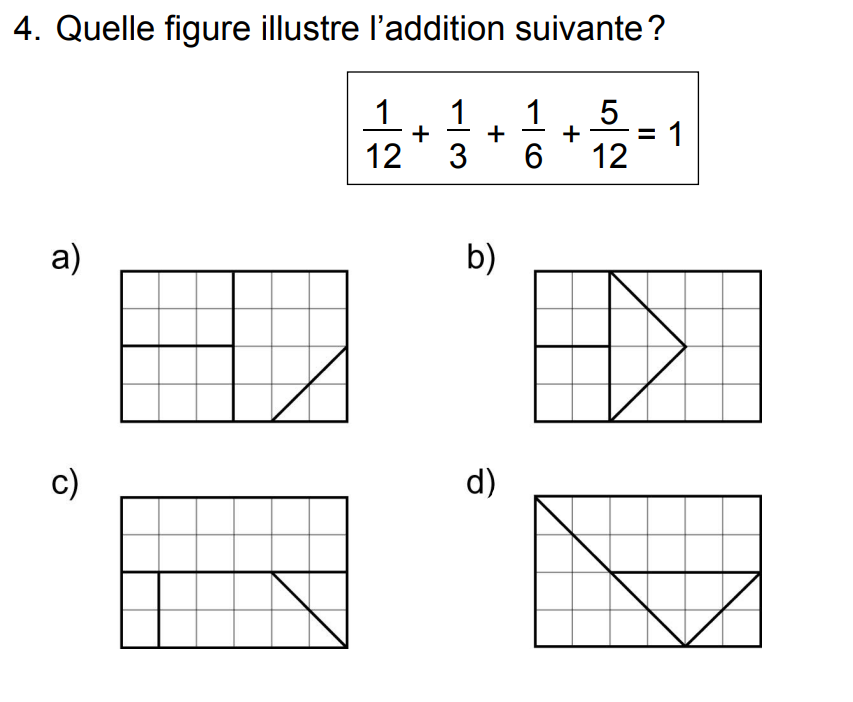
Dans cet exercice, le schéma représente l'addition de fractions. Le rectangle est divisé en quatre parties, chacune représentant l'une des fractions de l'addition!
Donc, pour réaliser cet exercice, tu dois tout d'abord considérer ce que représente ton "tout", soit ton dénominateur, dans la figure qui y est retrouvée (le rectangle). Si tu fais le décompte, tu remarqueras que cette figure rassemble 24 petits carrés.
Ensuite, tu devras mettre toutes les fractions sur le même dénominateur, soit 24!
Pour déterminer lequel des choix a), b), c) ou d) est le bon, tu devras associer chacune de tes fractions sur 24 à l'une des 4 parties du rectangle.
Par exemple, si l'on prend la fraction 1/12, elle devient 2/24. En effet, comme je dois multiplier le dénominateur par 2 pour obtenir 24, je dois également multiplier le numérateur par 2 pour conserver ma fraction équivalente! Ma nouvelle fraction, 2/24, sera donc représentée dans le rectangle par une partie de 2 petits carrés.
Je t'invite à consulter cette fiche, au besoin!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau! Continue tes efforts!
À bientôt,
Océane :)
Re: Question
Bonjour GalaxieTurquoise2162,
Merci d'avoir posé ta question à la Zone d'entraide.
Voici les étapes à suivre pour résoudre ce problème.
1-Multiplie le nombre de personnes par 1,5 (car chaque personne mange 1 ½ sandwich).
2-Multiplie le nombre de sandwiches par 2 (car chaque sandwich utilise 2 tranches).
3-Soustrais 2 tranches au total du nombre de tranches dans un pain (car on n'utilise pas les croûtes pour faire des sandwichs).
4-Divise le nombre total de tranches nécessaires (fait à l'étape 2) par le nombre de tranches utilisables dans un pain (fait à l'étape 3).
5-Arrondis vers le haut pour avoir un nombre entier de pains nécessaires.
J'espère t'avoir aidé. Bonne continuation!
Question
Bonsoir :)
J'espère que vous allez bien 😊!
En fait, j'ai de la difficulté à comprendre cet exercice, est-ce que vous pourriez s.v.p me donner un coup de main ?
Merci beaucoup ✨:D
Question
Re-bonjour !
En fait, j’ai un peu de difficulté à comprendre et à résoudre ce petit problème. Pourriez-vous, s’il vous plaît, m’aider à mieux le comprendre ?
Bonne soirée🌜!
Re: Question
BonjourPercheHonorable3167,
Merci d'avoir posé ta question à la Zone d'entraide!
La bourgeoisie marchande, c’est un groupe de personnes qui faisaient du commerce et vendaient des choses.
Grâce à eux :
-Il y avait plus d’argent dans les villes.
- Les villes grandissaient et offraient plus de travail.
- Ils pouvaient aider à construire des routes, des bâtiments ou soutenir les artistes.
- Ils avaient du pouvoir pour changer des règles.
Voici une fiche qui pourrait t'aider:
N'hésite pas à nous poser d'autres questions!
Re: Question
Salut PoissonRapide7685,
Merci d'avoir posé ta question à la Zone d'entraide!
Pour éviter d’avoir un blanc pendant ta présentation mardi, voici quelques conseils simples:
-Connais bien ton sujet, ça aide à parler naturellement.
-Prépare-toi de petites fiches avec les points clés, pas tout le texte.
-Entraîne-toi plusieurs fois, devant un miroir ou des amis.
-Si tu oublies, fais une pause et reprends calmement.
Voici des fiches présentant plusieurs astuces qui pourraient t'aider :
- Trucs pour préparer un exposé oral | Secondaire | Alloprof
- Apprendre à gérer son stress | Alloprof
- Gérer son stress et son anxiété liés à un exposé oral | Alloprof
- Trucs et astuces pour réduire le stress | Alloprof
J'espère t'avoir aidé. Je te souhaite bonne chance pour ton oral, tu es capable! ;)
Re: Question
Bonjour OrnithorynqueIntergalactique7407! :)
Merci pour ta question super intéressante!
En fait, la crainte de créer un trou noir avec un accélérateur de particules venait du fait que, lorsqu’on fait entrer deux particules en collision à très haute vitesse, certaines personnes pensaient qu’on pourrait reproduire un phénomène semblable à la mort d’une étoile, ce qui peut effectivement former un trou noir dans l’espace!
Mais rassure-toi! Même si des mini-trous noirs théoriques pourraient se former pendant ces expériences, ils seraient extrêmement petits, instables et disparaîtraient presque instantanément. Ils ne seraient pas dangereux pour nous.
Quant à ta question : « Pourquoi on ne teste pas où les choses aspirées dans un trou noir vont? », la réponse est que… personne ne le sait encore! On ne peut pas vraiment faire ce genre de test, parce que :
- Les trous noirs restent encore très mystérieux. La toute première "photo" d’un trou noir a été prise seulement en 2019!
- On ne peut pas "voir" ce qu’il y a à l’intérieur d’un trou noir, car même la lumière ne peut pas en sortir!
- On doit encore mieux comprendre leur fonctionnement, leur "anatomie" et leur formation avant d'imaginer les utiliser pour des expériences comme celle que tu proposes.
Mais qui sait? Peut-être qu’un jour, grâce aux scientifiques comme toi, on pourra aller plus loin!
Si tu as d’autres questions, n’hésite surtout pas à revenir nous voir!
Bonne journée! :D
Re: Question
Bonjour IguanodonFiable1438! :)
Merci pour ta question!
En fait, dans un problème d’optimisation, l’ordre des variables (par exemple x et y) n’a pas vraiment d’importance. C’est vrai que le graphique peut changer un peu selon leur position, mais au final, ce qui compte, ce sont surtout les points d’intersection entre tes droites frontières. Ce sont eux qui permettent de trouver la solution optimale!
Par contre, un élément très important, c’est que les coefficients de A et B soient bien placés dans ton équation à optimiser (comme max Z = Ax + By). Si ce n’est pas le cas, tu risques de ne pas arriver à la bonne réponse, même si ton graphique est bon!
J’espère que ça t’aide! :) Si tu as d’autres questions, n’hésite surtout pas à revenir nous voir!
Bonne journée! :D
Re: Question
Bonjour AvocatRaisonnable6203! :)
Merci pour ta question! :D
Commençons par établir les équations des forces qui agissent sur chaque bloc.
Pour le bloc A, il subit deux forces principales :
- la tension (T) de la corde,
- la force de frottement cinétique (fk).
Son équation devient donc :
T - fk = mA × a
(Ici, "a" représente l'accélération commune aux deux blocs.)
Pour le bloc B, il subit :
- la force gravitationnelle (le poids),
- la tension (T), qui agit vers le haut.
Son équation devient :
mB × g - T = mB × a
Maintenant, remplaçons par les valeurs données! :D
Pour le bloc A:
T - 5.7 = 2.7 × a
Pour le bloc B :
(3.7 × 9.8) - T = 3.7 × a
Ce qui donne :
36.26 - T = 3.7 × a
Pour trouver a, il faut faire disparaître la tension (T) pour pouvoir trouver l'accélération (a).
Additionnons :
(T - 5.7) + (36.26 - T) = 2.7a + 3.7a
Les T s'annulent, et on obtient :
30.56 = 6.4a
On peut donc calculer :
a = 30.56 ÷ 6.4 ≈ 4.77 m/s²
Une fois l'accélération trouvée, on peut revenir à l'une des deux équations (celle du bloc A ou B, peu importe) pour trouver la tension T.
Par exemple, en reprenant :
T - 5.7 = 2.7 × a
Remplace le "a" par la valeur trouvée, et tu auras T!
J’espère que ça t’aide! N’hésite pas à revenir nous voir si tu as d'autres questions! :D
Bonne journée et bon travail!
Re: Question
Bonjour ElfeMauve5850! :D
Merci pour ta question!
Malheureusement, nous n’avons pas encore d’exercices disponibles sur les textes expressifs.
Mais si tu veux, tu peux nous envoyer un exercice que tu as moins bien réussi, et on pourra le travailler ensemble! Ce sera un bon moyen de t’améliorer.
Si jamais tu as d’autres questions, n’hésite surtout pas à revenir nous voir!
Bonne journée et bon travail!