Best Of
Re: Question
Bonjour,
En général, les pros de la Zone doivent être des élèves du deuxième cycle du secondaire. Je t'invite donc à nous réécrire plus tard dans notre parcours scolaire!
Même si tu n'es pas pro, tu peux tout de même répondre aux questions des autres élèves. Nous t'encourageons à essayer! :D
En ce qui concerne la Zone en anglais, tu peux changer la langue en haut à gauche de ton écran! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour FraiseComique6111,
Merci d'utiliser la zone d'entraide. :)
Tout d'abord, pour vouloir travailler, je te suggère fortement d'avoir un emploi que tu aimes. Cela va te motiver à te lever chaque matin pour aller travailler. N'oublies pas que le travail est l'endroit où tu passes le plus de temps lorsque tu es adulte, c'est donc important d'y être confortable et d'apprécier son travail. Tu es encore jeune pour trouver un emploi qui te motives et c'est tout à fait normal.
Explore tes intérêts et tes qualités. Si tu aimes aider les autres, peut-être que tu pourrais être infirmier ou infirmière ? Si tu aimes travailler avec tes mains peut-être que tu peux travailler en construction ? Il y a de multiples avenues qui s'offrent à toi. :)
Ensuite, tu dois te déterminer quelques objectifs. Pas besoin que ce soit énorme. Ça peut être :
- Voyager
- Te payer un loisir (une passe de ski, un vélo, etc.)
- Aider ta famille
- Aller à l'université
- Économiser pour ta retraite
- Te payer une voiture
- Te payer un logement
- etc.
Enfin, il existe plusieurs façon d'économiser. Je te suggères de te faire une feuille qui calcul tes revenus (l'argent que tu reçois) et des dépenses (ton cellulaire, par exemple) et ainsi calculer combien il te reste et combien tu peux mettre de côté pour chacun de tes objectifs.
Voilà ! J'espère que cela répond à ta question.
N'hésite pas à repasser si tu as d'autres questions ! :)
Angélique
Re: Question
Salut à toi intrépide prodige! 😁
Ça nous fait plaisir que tu utilises Alloprof!
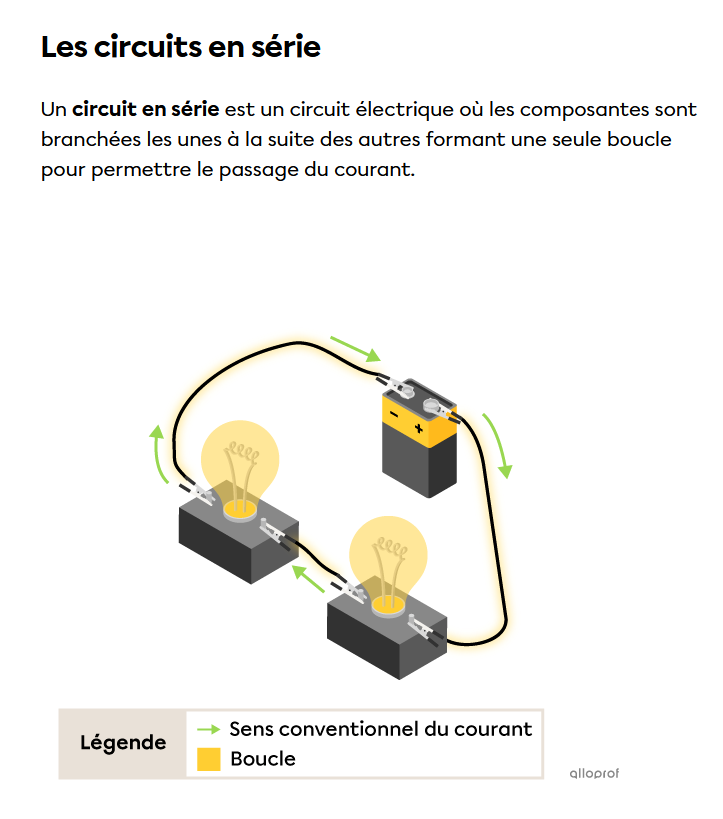
Une des caractéristiques du circuit en série est que l’intensité du courant est la même dans toutes les composantes du circuit.
Tu peux donc brancher l'ampèremètre où tu veux, tu obtiendras la même mesure. Apprends-en plus sur les branchements des outils de mesure ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut à toi intrépide prodige! 😁
Ça nous fait plaisir que tu utilises Alloprof!
D'abord, voici quelques ressources à étudier.
Le nez
La langue
La peau
Le système musculosquelettique
Pour savoir comment les étudier, je te donne quelques astuces. Faire une feuille de notes avec les informations importantes sur chacun des systèmes te permettra de commencer à réviser en résumant l'information, et te servira d'outil d'étude pour les fois à venir. C'est ma manière d'étudier préférée! Sinon, il y a aussi des fiches questions-réponses que tu peux faire (les détails sont dans l'article au bas). Faire un exposé sur le sujet à tes parents ou à un.e ami.e peut aussi être un excellent moyen pour apprendre la matière.
Il y en a plus ici!
Mémorisation et concentration
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour TortueOrange9884,
Merci d'utiliser Allo prof ! Je comprends que le stress d'avoir une bonne note en examen est très préoccupant (j'imagine que tout le monde pense comme toi !).
J'aimerais bien t'aider mais est-ce que tu peux donner plus de précisions sur la matière que tu veux réviser ?
À bientôt sur la Zone d'entraide,
PandaSolidaire1774
Re: Question
Bonjour BB8Incomparable3278! :)
Merci pour ta question! 😊
Les concessions accordées aux Canadiens français ont eu des conséquences majeures sur les deux partis politiques de l’époque : le French Party et le British Party.
Du côté du French Party, ces concessions ont permis de protéger la culture canadienne-française. La langue française, les lois civiles françaises, la religion catholique et les traditions ont été conservées. Pour eux, c’était une forme de reconnaissance et une façon de préserver leur identité, malgré la conquête britannique.
En revanche, le British Party, qui représentait la minorité anglophone et les intérêts britanniques, a vu ces concessions comme un recul de l’autorité britannique. Elles étaient perçues comme une menace à leur pouvoir et un frein à l’assimilation des Canadiens français.
Ces mesures, qui avaient pour but de créer un équilibre entre les deux groupes, ont plutôt augmenté les tensions. Cette opposition croissante entre les deux partis a contribué à la crise politique qui a mené à la Rébellion des Patriotes en 1837-1838.
Si tu veux en savoir plus, je te recommande les fiches historiques disponibles sur le site de l’Assemblée nationale du Québec!
https://www.assnat.qc.ca/fr/patrimoine/lexique/french-party-%28parti-francais%29.html?
J’espère que ma réponse t’a aidé à mieux comprendre! :)
Si tu as d’autres questions, n’hésite surtout pas à revenir nous voir!
Bonne journée! :D
Question
Bonjour, j'ai une question pour mon cours de chimie organique.
J'ai de la difficulté à identifier si une substance est plus soluble dans du H2O ou du dichlorométhane.
Par exemple, pour le salicylate de méthyle, j'ai trouvé qu'il a une masse molaire (152,15 g/mol) plus près de celle du dichlorométhane que celle de l'eau, et qu'il est polaire. J'ai aussi trouvé que cette molécule peut faire des ponts hydrogènes avec l'eau. Ces informations m'indiquent des réponses opposées, donc je ne suis pas certaine de la réponse qui est juste.
J'ai le même problème avec le salicylate de sodium. Sa masse molaire est plus proche de celle du dichlorométhane, mais il peut faire des ponts hydrogènes avec l'eau.
Merci d'avance!
Question
Bonjour Alloprof,
Je fait souvent des opérations mathématique en passe temps et j'achète des livre de calcul avancé.
Je suis tombé en réflexion sur une questions que j'ai du mal à répondre et je chercherais une explication.
Voici la question :
Je sais que f(x)=∫0xtsin(t2) dtf(x) = \int_0^x t \sin(t^2) \, dtf(x)=∫0xtsin(t2)dt, donc pour x→0x \to 0x→0, la fonction ne présente pas de singularité, et elle reste bien définie. Elle est continue et tend vers 0 quand xxx approche 0,Quand xxx devient très grand, je remarque que sin(t2)\sin(t^2)sin(t2) oscille entre -1 et 1, et cela signifie que f(x)f(x)f(x) va osciller aussi. Cependant, l'amplitude des oscillations ne diminue pas assez rapidement pour que l'intégrale converge. En fait, l'intégrale ∫0∞f(x) dx\int_0^\infty f(x) \, dx∫0∞f(x)dx risque de diverger.Mais c'est pour la suite que j'ai de la misère
Merci,
GiganotosaureIntergalactique9154
Re: Question
Salut! J'ai trouvé une explication, j'espère pouvoir t'aider!
D'accord, tu as bien analysé le comportement de la fonction \( f(x) = \int_0^x t \sin(t^2) \, dt \). Je vais t’aider à approfondir la question sur la divergence de l’intégrale \( \int_0^\infty f(x) \, dx \).
1. **Comportement de \( f(x) \) pour \( x \to \infty \)
Comme tu l’as remarqué, la fonction \( \sin(t^2) \) oscille entre \(-1\) et \(1\). Cela entraîne des oscillations dans \( f(x) \), mais la clé ici est de voir si \( f(x) \) tend vers zéro suffisamment rapidement pour que l’intégrale de \( f(x) \) converge.
En utilisant l’intégration par parties avec \( u = t \) et \( dv = \sin(t^2) dt \), on pourrait obtenir une approximation du comportement asymptotique de \( f(x) \). En général, l’intégrale de \( t \sin(t^2) \) ne tend pas vers zéro assez vite pour que l’intégrale impropre de \( f(x) \) soit convergente.
2. Examen de la convergence de \( \int_0^\infty f(x) \, dx \)
L’un des moyens les plus efficaces de déterminer la convergence est d’étudier le critère de comparaison avec une fonction dont on connaît déjà le comportement.
Si \( f(x) \sim x \) pour \( x \to \infty \), alors \( \int_0^\infty f(x) \, dx \) aurait tendance à diverger comme \( \int_0^\infty x \, dx \), qui est bien connu pour être divergent.
Un raisonnement plus rigoureux peut impliquer une analyse asymptotique des oscillations et une étude de la moyenne de \( \sin(t^2) \) sur des intervalles de grande taille.
3. Que faire pour la suite ?
Si tu veux une preuve formelle de la divergence, il faudrait examiner si \( f(x) \) décroît suffisamment rapidement ou non en utilisant un critère d’intégrabilité comme celui de Dirichlet ou des tests de convergence de séries intégrales.
Un moyen rapide serait de vérifier si \( f(x) \) est bornée par une fonction qui est connue pour être divergente.