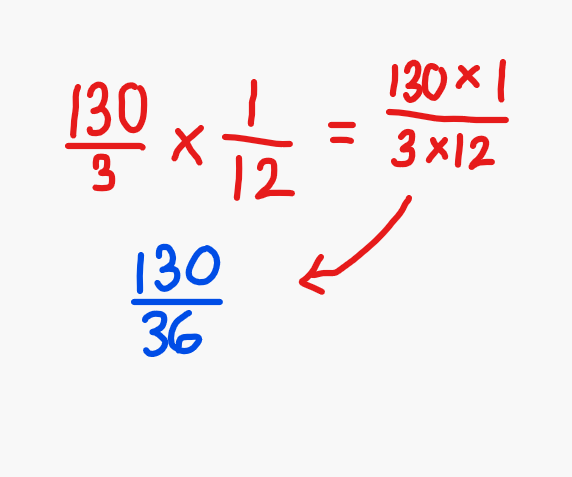Best Of
Re: Question
Salut a toi,
Moi aussi j'ai un TDAH et je comprend ta misère. J'ai quelque truc qui pourrait t'aider.
- Transformer ce que tu dois te souvenir en chanson qui te reste pogné dans la tete.
- Révise une dernière fois avant un exam et écris toi dans un coin de ta feuille toute les choses don tu te souviens. Ca vas te permettre de pouvoir réfléchir sans avoir besoin de retenir toute l'info tout le long.
- Réécrit, meme si je sais parfois c'est vraiment plate de toute devoir réécrire c'est l'une des meilleures façon de se souvenir de choses.
J' espère que cela va t'aider dans ta mémorisation !
Pistache
Re: Question
Salut,
Merci de nous faire confiance.
Il est très normal d'avoir de la difficulté à se concentrer dans cette situation. Plusieurs astuces sont présentes pour t'aider.
Voici un lien avec des trucs :
Pour favoriser la mémorisation, le secret est la pratique! La répétition permet au cerveau d'enregistrer plus profondément certains éléments que l'on souhaite apprendre.
Pour améliorer la mémorisation d'une certaine matière, il faut donc étudier d'avance et s'assurer de bien comprendre les concepts impliqués et non de tout apprendre par cœur. Pour ce faire, il est possible d'utiliser des trucs mnémotechniques, qui lient des concepts à des mots ou des choses que nous connaissons déjà.
Il peut être utile d'utiliser plusieurs de tes sens lorsque tu étudies. Par exemple, il peut être intéressant de réécrire, de relire et de dire à voix haute une notion que tu souhaites assimiler. Cela permet à ton cerveau d'ancrer cette information de plusieurs manières.
De plus, je te suggère grandement de parler de tes questionnements avec ton enseignant, je suis certaine qu'il pourra te donner des conseils spécifiquement pour t'aider avec tes difficultés.
N'hésite pas à revenir nous voir.
Karen
Re: Question
Bonjour R2D2Iota9883,
Merci beaucoup pour ta question! Je ne suis pas tout à fait certaine de bien comprendre ton questionnement face à cette situation. En effet, je ne vois rien qui cloche dans l’image et dans tes propos. Il est vrai de dire qu’aucune image réelle ne sera produite, puisque les deux rayons sont parallèles. L’œil humain ne peut pas observer ce type d’image. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Tu as peux-être des difficultés en français (tels que de la dyslexie qui fait en sorte que ton cerveau confond des lettres et rends donc l’écriture plus difficile). Il n’y a rien de mal à en avoir (même que c’est très courant chez les enfants) mais il est primordial d’être bien accompagné pour t’aider à surmonter tes difficultés ! Si tu penses en avoir, demande à tes parents de consulter un orthopédagogue.
En espèrant t’avoir aidé 😉
HirondelleTurquoise 🐦💙
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
C'est une bonne question.
En fait, on dit « Acte de Québec » parce que c’est le nom officiel donné à une loi faite par la Grande-Bretagne en 1774. On ne parle pas dans ce titre d'un acte qui appartient au Québec, mais plutôt, d'une loi qui parle du Québec. C'est pour cette raison que l'on utilise le de plutôt que le du.
J'espère t'avoir aidé à mieux comprendre,
À bientôt,
Karen
Re: Question
Bonjour!
Il est possible de poser des questions en lien avec la politique. Évidemment, ces questions doivent rester respectueuses et sérieuses.
N'hésite pas si tu as d'autres questions! :D
Laurie :)
Re: Question
Salut!
Je vais commencer avec 1/12 de 130/3 (en passant, tu as raison, on te demande bien de diviser). Premièrement, tu dois savoir qu'en maths, lorsqu'on te dit «de», ça veut dire que tu dois faire une multiplication. Ainsi:
1/12 de 130/3 = 1/12 x 130/3
Lorsqu'on multiplie une fraction par une autre fraction, on multiplie les numérateurs (les chiffres en haut) ensemble et on multiplie les dénominateurs (les chiffres en bas) ensemble comme ceci:
De plus, je ne sais pas si ton professeur te demande de faire ça, mais si tu dois simplifier ta fraction, tu peux constater ici que le numérateur (130) et que le dénominateur (36) se divisent tous les deux par 2. Donc, tu peux faire 130 ÷ 2 = 65. Et tu peux faire 36 ÷ 2 = 18. Ta fraction simplifiée est donc de 65/18.
--> Si tu as une calculatrice, calcule 130 ÷ 36, puis calcule 65 ÷ 18. Ça devrait te donner le même résultat! Simplifier une fraction permet juste de l'exprimer avec des nombres plus petits (donc plus simples).
Es-tu capable de calculer 1/9 de 81/3, maintenant?
J'espère t'avoir aidé.e! :)
Re: Question
Bonjour, merci pour ta question, TigreHumble1318!
L'échelle est le rapport entre les dimensions d'un objet sur un dessin et les dimensions d'un objet dans la vraie vie.
Puisqu'il s'agit d'un rapport, on l'écrit sous la forme suivante :
$$ dimension\:sur\:le\:dessin\: : \:dimension\:réelle $$
Il faut toujours qu'un des deux termes dans le rapport soit égal à 1.
Pour trouver l'échelle dans ce numéro, il faudra que tu mesures avec une règle une des dimensions du prisme (forcément la longueur ou la hauteur, puisque la profondeur est à angle avec toi) sur le dessin et que tu la compares à ses dimensions écrites. Par exemple, si la longueur réelle est de 0,05 m (5 cm), le rapport sera de :
$$ \frac{0,05\:m}{0,75\:m}=\frac{1}{15}=1:15 $$
Voilà!
Cette fiche du site d'Alloprof parle de l'échelle :
N'hésite pas si tu as d'autres questions!
Re: Question
Salut, Amael!
Tu as la bonne formule, soit :
Et tu as bien placé chacune des variables énoncées dans le problème.
Cependant, n ≠ 5 ans. En effet, l'énoncé mentionne qu'il y a un taux d'intérêt semestriel, et non annuel. Il faut donc trouver le nombre de semestres qu'il y a en 5 ans. Puisqu'un semestre a une durée de 6 mois, il y a donc 2 semestres par année, et donc 10 semestres en 5 ans. Ainsi, n = 10
Maintenant, il ne te reste plus qu'à isoler la variable i, soit le taux d'intérêt composé semestriel, comme ceci :
$$ 8144,47 = 5000 (1+i)^{10} $$
$$ \frac{8144,47}{5000} = (1+i)^{10}$$
$$ \sqrt[10]{\frac{8144,47}{5000}} = \sqrt[10]{(1+i)^{10}} $$
$$ \sqrt[10]{\frac{8144,47}{5000}} = 1 + i $$
$$ \sqrt[10]{\frac{8144,47}{5000}} -1 = i $$
$$ i ≈ 0,05 $$
Le taux d'intérêt composé semestriel est donc de 5%.
Voici une fiche sur cette notion qui pourrait t'être utile :
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-taux-d-interet-compose-m1571
N'hésite pas si tu as d'autres questions, et bon succès pour ton examen! :)