Best Of
Question
Bonjour,
quelle était la situation socio-économique des francophones en 1965?
merci pour votre aide!
Question
Je ne sais pas comment faire la question 5 et pourquoi k a question 4 quelle est le sens des crochets, car j’ai demandé à IA il m’a dit ]-15,-10] mais b>0 donc c’est pas supposé être ouverte vers la droite et ferminé gauche?
Question
Je ne sais pas comment faire la question 5 et pourquoi k a question 4 quelle est le sens des crochets, car j’ai demandé à IA il m’a dit ]-15,-10] mais b>0 donc c’est pas supposé être ouverte vers la droite et ferminé gauche?
Question
Bonjour allôprof
Est-ce que le x¹ et y¹ peuvent être (12,25) ou (22,10). Je pense que mon prof m'a dit ça au début de l'année que ça dépendu où le x¹ et y² peut être et je suis confu merci
Question
Bonjour allôprof s'il y un point plein le bleu Est ce que ce que je met crochet fermé ou ouvert et si c'est point vide est ce que je mets point vide ou point fermé?
Question
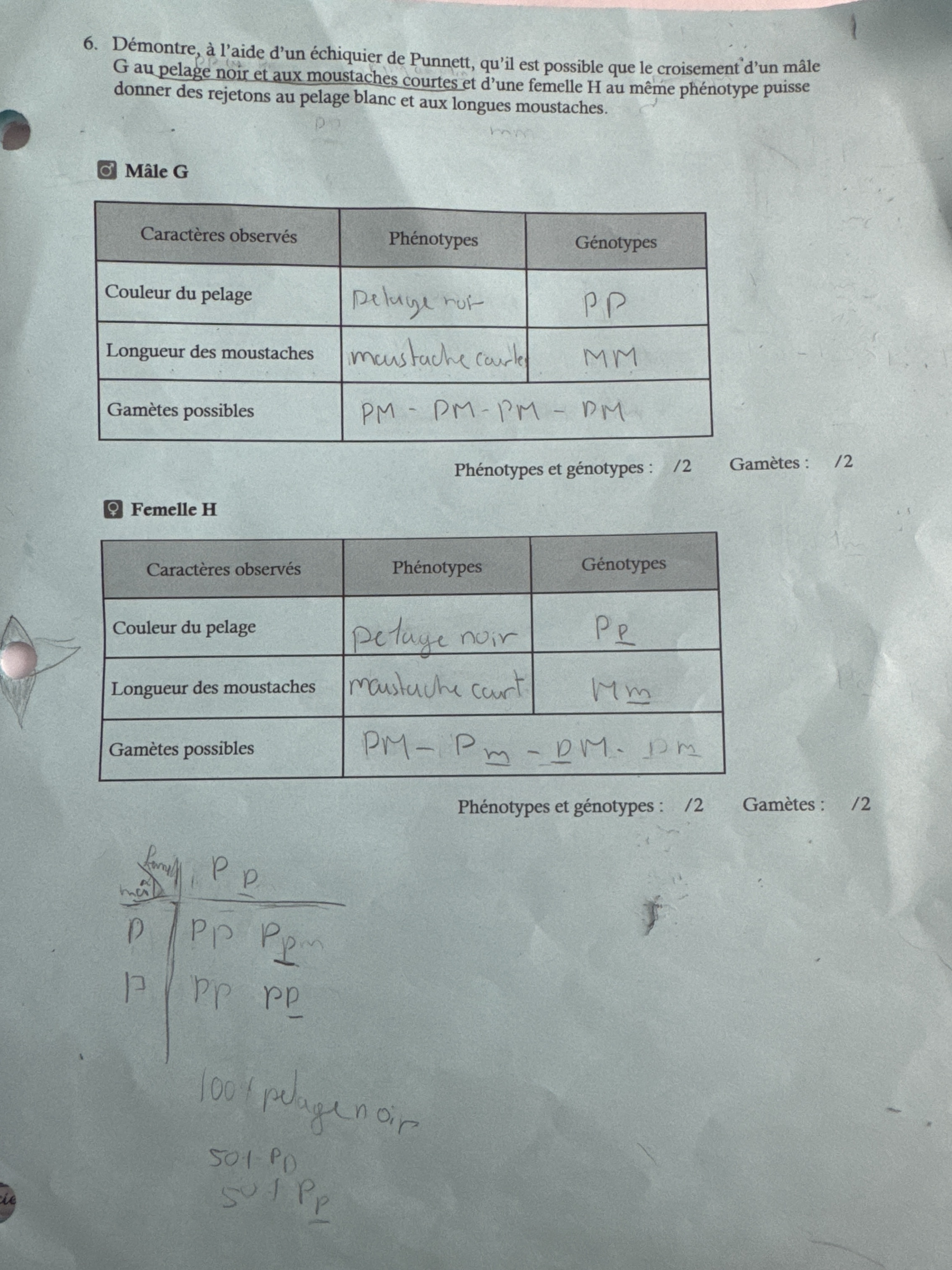
Bonjour j’avais déjà poser une question sur ce sujet, mais j’en ai une autre. Je voulais savoir si c’est le mâle et la femelle qui doivent donner des rejetons au pelage blanc et longues moustaches ou c’est juste la femelle?
Question
bonjour jai un examen de geographie sec 2 module 10 completement geo et mon enseignant va me posser une grosse question entre les differences du territoire de sahel et dun autre territoire ou il me fournira des document et la duree est de 70min alors peut tu me posser une question comme celle la Décrire les principales caractéristiques de chacun des territoires (climat, type d’agriculture, ressources disponibles, etc.). Expliquer les risques auxquels l’agriculture est confrontée dans chacun (sécheresse, urbanisation, érosion, etc.). Présenter et comparer les aménagements mis en place pour répondre à ces risques. Analyser les effets de ces risques sur la sécurité alimentaire et la population locale. Donner ton opinion sur lequel des deux territoires est le plus vulnérable, avec des arguments clairs.