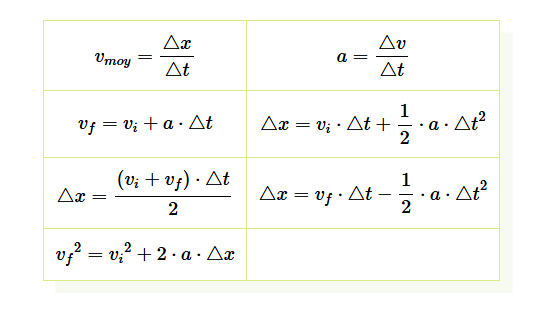Best Of
Re: Question
Bonsoir, DiplodocusOrange3310!
Tu as assez bien illustré la situation, félicitations!
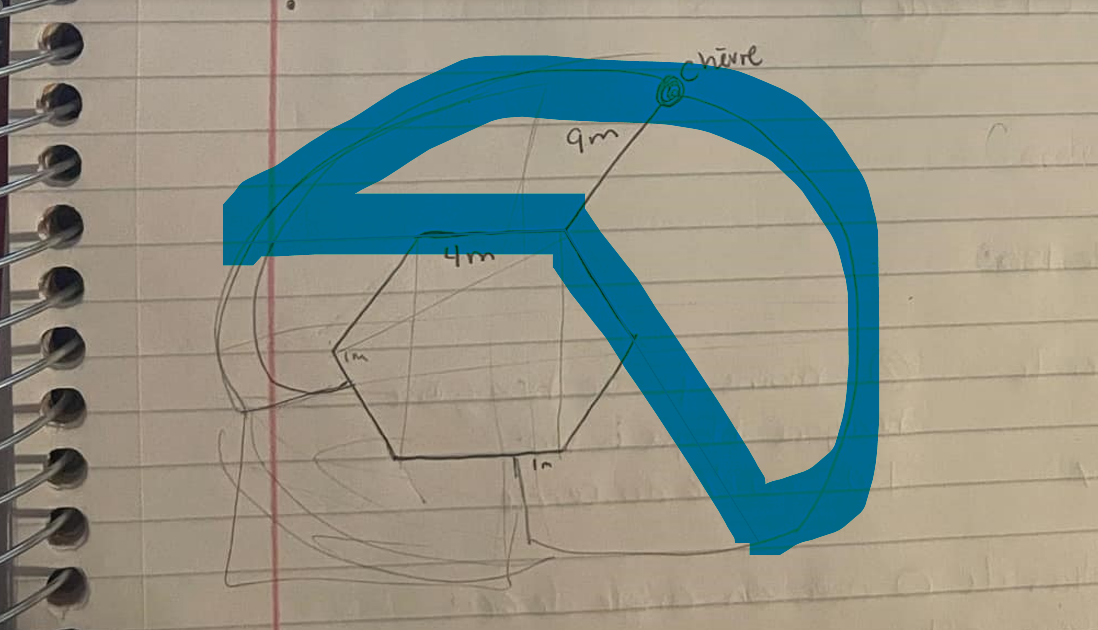
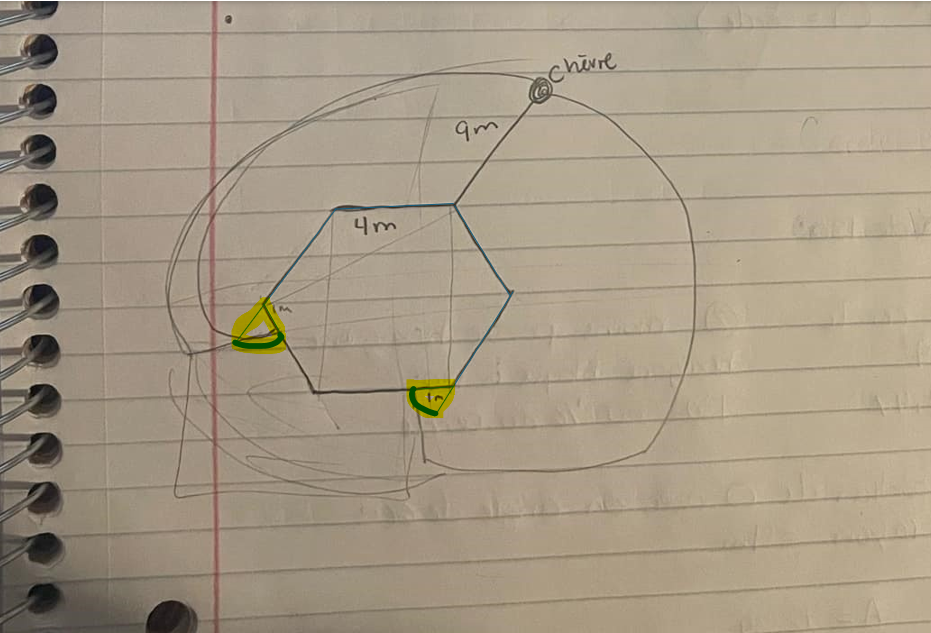
On peut séparer l'aire atteinte en différents secteurs de disques.
Secteur 1
On calcule l'aire du premier secteur provenant d'un disque ayant comme rayon 9 m.
$$ \dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}} $$
«L'angle au centre» est en fait l'angle extérieur de l'hexagone. Pour le trouver, on calcule d'abord l'angle intérieur selon la formule ci-dessous, puis on soustrait cette valeur de 360 pour connaître l'angle externe.
$$ \begin{align}\text{Mesure d'un angle intérieur}&= \frac{\text{somme des angles intérieurs}}{\text{nombre de côtés du polygone}}\\ &= \frac{(n - 2) \times 180^\circ}{n}\end{align} $$
Secteur 2
Les deuxièmes secteurs ont un rayon de 5 m et un angle extérieur (l'angle compris entre un côté et le prolongement du côté adjacent) de l'hexagone.
$$ \begin{align}\text{Mesure d'un angle extérieur}&= \frac{360°}{\text{nombre de côtés du polygone}}\\ &= \frac{360°}{n}\end{align} $$
Secteur 3
L'aire des derniers secteurs est calculée avec l'angle précédent, mais le rayon est de 1 m cette fois.
N'hésite pas à poser d'autres questions!
Re: Question
Bonjour QuetzalRaisonnable7843,
Merci pour ta question :)
Tu arrives avec raison à l'équation y=-6-3x. Pour mettre le -3x en premier, il suffit de réorganiser les termes de l’équation tout en gardant leurs signes respectifs. Cela donne : y=-3x-6. Il n’y a pas besoin de changer de signe quand on réorganise les termes, à condition de ne pas effectuer d’opération supplémentaire (comme multiplier ou diviser): le terme -3x reste -3x et -6 reste -6 :)
Si tu as besoin de consulter des exemples de résolutions avec la méthode de substitution, je t'invite à consulter la page suivante: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-methode-de-substitution-m1088
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Salut!
Le caillou est en chute libre. En d'autres mots, l'objet est dans les airs et ne subit aucune autre force autre que celle de la gravité.
Ainsi, l'accélération du caillou est constante, elle correspond à l'accélération gravitationnelle. Donc, l'objet effectue un mouvement uniformément accéléré (MRUA).
On peut donc utiliser les équations associées aux MRUA :
On connait la vitesse initiale (\(v_{i}=4,0m/s\)), l'accélération (\(a=9,8m/s^2\)), et la variation de temps (Δt=2 s). On cherche la profondeur, donc la distance parcourue Δy. Quelle équation fait intervenir ces variables? Je te laisse la trouver :)
Si tu as d'autres questions, n'hésite pas!
Re: Question
Bonsoir, GalaxieRapide5770!
D'abord, on transforme le pourcentage en fraction.
60% = 60/100
Ensuite, on peut réduire la fraction.
60/100 --> 3/5
La situation implique une multiplication.
3/5×X=30
On fait l'opération inverse (division) pour trouver la valeur de X.
3/5×X=30 -->
X = 30 ÷ 3/5
On inverse la fraction.
X = 30 × 5/3
On calcule.
(30×5=150, 150÷3= 50) ou plus facilement (30÷3=10, 10×5=50)
Donc, la réponse est X=50.
Re: Question
Bonjour FraiseAdorable5247, merci pour ta question !
Il est vrai que ces exemples peuvent un peu prêter à confusion. La règle d'usage est que si tu dois citer une enthalpie molaire, il faut citer la substance à laquelle tu fais référence. J'ai l'impression que dans le a), l'enthalpie molaire correspond au lithium ou au HCl.
Avec seulement l'image que tu m'as fourni, je suis d'avis qu'il n'est pas vraiment possible d'attribuer correctement l'enthalpie molaire à la bonne substance. Peut être que l'information se trouve ailleurs sur le document ?
Quoi qu'il en soit, je te recommande de toujours préciser à quelle substance appartient l'enthalpie molaire que tu cites, justement pour éviter ce genre de confusion justement.
N'hésite pas à nous écrire si tu as d'autres questions !
Re: Question
Salut!
On te donne une table de valeurs incomplète. Pour la compléter, tu dois utiliser la coordonnée déjà donnée ainsi que la règle de la fonction.
Par exemple, tu dois trouver f(x) (la coordonnée en y) pour x=10. Pour ce faire, tu dois résoudre cette équation pour trouver f(10) :
$$f(10)=2,5(10)+4$$
Si on te donne f(x) et que tu cherches x, c'est le même principe. Par exemple, on cherche x lorsque f(x)=79. Tu dois donc résoudre cette équation pour trouver x :
$$79=2,5x+4$$
Je te laisse essayer avec ces indices. Voici une fiche qui pourrait t'être utile : La résolution d'équations et d'inéquations | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! :)
Re: Question
Bonjour LoupRomantique!
Merci pour ta question :)
Albert Einstein était un physicien théoricien d'origine allemande, souvent considéré comme l'un des plus grands génies de l'histoire. Il est né le 14 mars 1879 à Ulm, en Allemagne, et mort le 18 avril 1955 à Princeton, aux États-Unis, Einstein est surtout célèbre pour sa théorie de la relativité, qui a transformé notre compréhension de la physique, du temps et de l'espace.
Si tu as d'autres questions, n'hésite pas à nous revoir :)
DiamantAuthentique
Re: Question
Salut!
Pour apprendre tes tables de multiplication, il n'y a vraiment qu'un seul moyen, la PRATIQUE! ;) Le secret est de se pratiquer le plus possible, et tu verras que bientôt, tu les réciteras comme sur le bout de tes doigts!
Voici des jeux qui te permettront de pratiquer tes tables tout en t'amusant : Météormath et Fin Lapin.
Je te conseille aussi d'aller jeter un coup d'œil à la fiche suivante, tu y trouveras diverses astuces pour t'aider à apprendre tes tables par cœur : Trucs pour apprendre les tables par coeur | Alloprof
De plus, sur ce site, tu trouveras des astuces pour chacune des tables de multiplication, tu n'as qu'à cliquer sur la table souhaitée : https://universites-numeriques.fr/table-de-multiplication/
En les révisant régulièrement, je suis sûre que tu deviendras un pro très rapidement! À toi de jouer maintenant! :D
Question
allo
jai des problaime avec mon francais ecriture et lecture pouver vous me donner des truc
Re: Question
Bonjour CannebergeSympatique!
Merci pour ta question :)
La lithosphère est la couche externe solide de la Terre. Elle comprend la croûte terrestre et la partie supérieure du manteau terrestre, qui sont rigides.
La lithosphère est très importante pour la vie, car elle constitue les sols, qui sont nécessaires à la croissance des plantes et végétaux qui sont à la base de la chaîne alimentaire.
Voici un lien qui te seras utile :)
J'espère que cela t'as aidé!
DiamantAuthentique