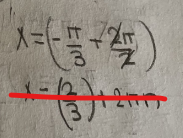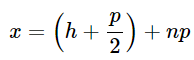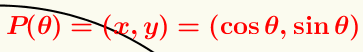Populaires
Re : Question
Salut !
La première étape serait de trouver l'angle A.
$$ tan^2A=(tanA)^2=2 $$
$$ tanA=\sqrt{2} $$
Par la suite, tu peux utiliser l'identité trigonométrique pour trouver la valeur finale :
$$ sec^2A=\frac{1}{cos^2A}=? $$
Si tu as d'autres questions, n'hésite pas !
Re : Question
L'artère rénale est aussi l'aorte ("la continuité").
Elle subit une plus grande pression de la contraction du coeur, qui lui doit propulser le sang dans tout le corps (circulation systémique). Donc, elle doit être capable de se contracter/d'être extensible.
Alors que la veine rénale ramène le sang (avec des déchets) vers le coeur et ne subit autant de pression.
J'espère que ça répond à ta question :)
Re : Question
Re-bonjour Ara Enthousiaste!
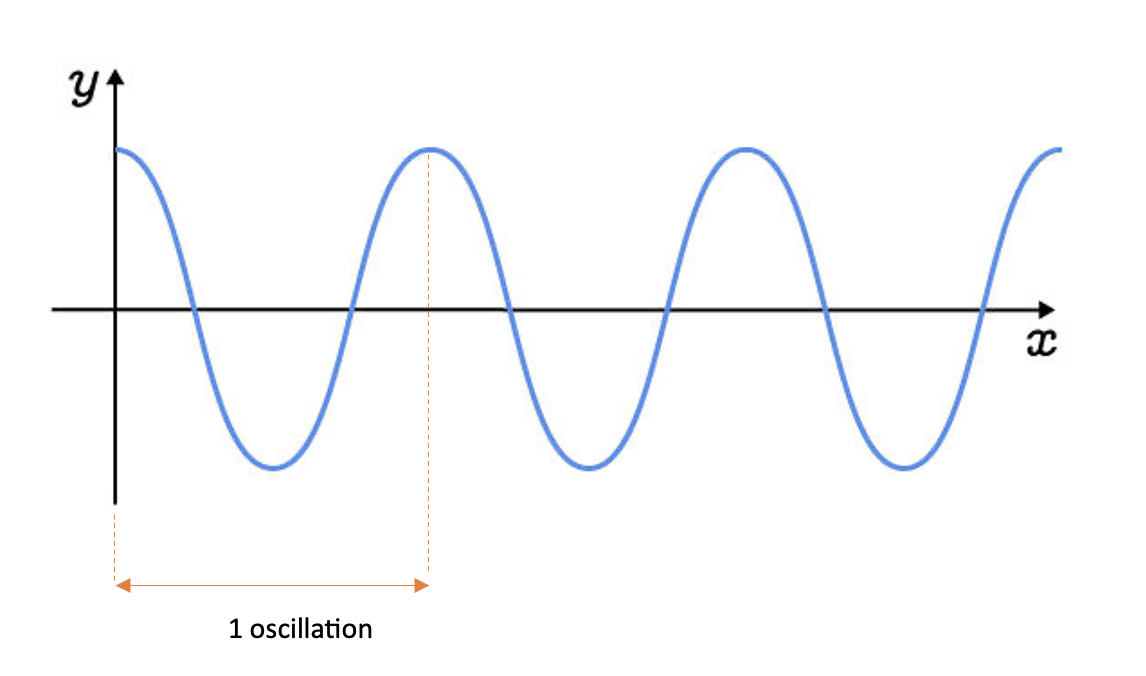
Lorsque nous parlons d'ondes, une oscillation représente le cycle complet d'une onde. Voici une représentation:
Pour la deuxième question, l'image représente deux oscillations sur une distance de 114m. Ainsi, d = 114 m et N = 2.
Il faut donc diviser 114 par 2 pour trouver la longueur d'onde.
Pour réviser les caractéristiques des ondes et des exemples de calcul, tu peux consulter la fiche explicative suivante:
J'espère que cela t'aidera!
Re : Question
Salut!
Tu as trouvé la bonne période, soit 2π, ainsi qu'un zéro de la fonction, soit \(x= \frac{4π}{3} \).
Cependant, tu as fait une petite erreur de calcul lorsque tu as calculé l'équation pour les asymptotes.
Ton calcul était bon jusqu'ici :
Tu as ensuite effectué l'addition \(x=\frac{-\pi}{3}+\pi \), mais tu étais censé obtenir \(x=\frac{2\pi}{3} \) et non \(x=\frac{2}{3} \).
L'équation des asymptotes est donc \(x=\frac{2\pi}{3} + 2\pi n\)
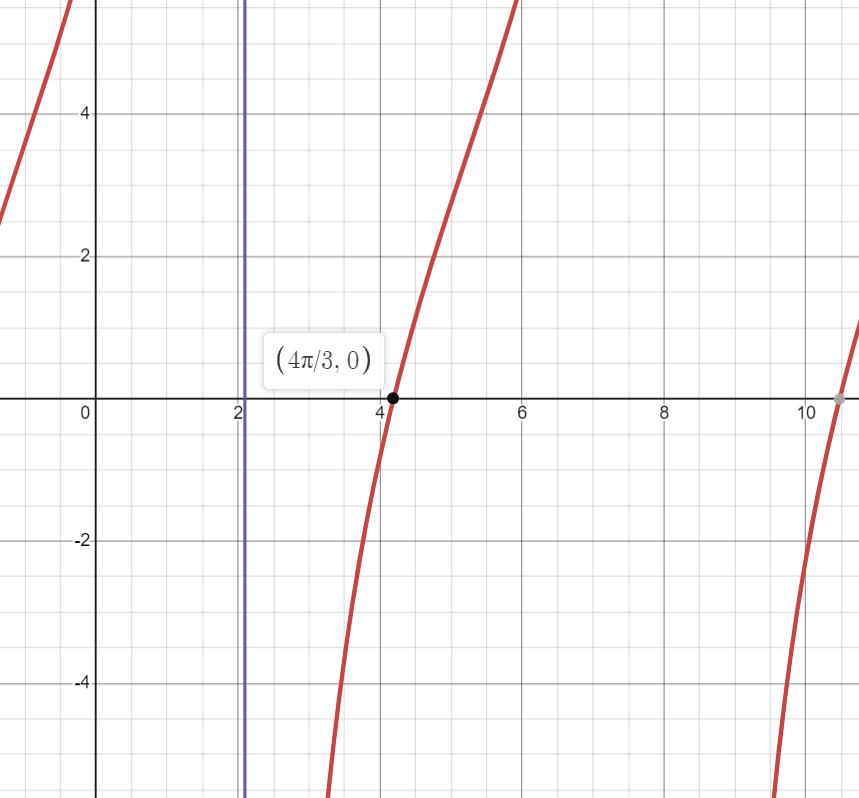
Ensuite, tu dois tracer ta fonction afin de déterminer l'intervalle pour lequel la fonction est négative. En traçant le graphique, on peut constater que la fonction (en rouge) est négative d'une asymptote (en mauve) jusqu'au zéro suivant, telle que \(x= \frac{4π}{3} \) :
Tu n'as plus qu'à combiner l'équation de l'asymptote ainsi que le zéro qui la suit à droite afin d'exprimer l'ensemble-solution de l'inéquation, comme ceci : ]\( \frac{2\pi}{3} + 2\pi n, \frac{4π}{3}+ 2\pi n\)] où \(n\) ∈ \( \mathbb{Z} \).
Tu trouveras des exemples similaires ici : Résoudre une équation ou une inéquation trigonométrique | Alloprof
De plus, je t'invite à consulter la fiche suivante pour t'aider à tracer la fonction : Tracer une fonction tangente | Secondaire | Alloprof
Tu peux également te servir du logiciel Desmos afin de valider tes dessins : Desmos | Calculatrice graphique
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Reste à faire une esquisse graphique et à trouver les asymptotes avant et après la valeur de 4pi/3 .
Re : Question
Un banc pour 22 personnes?
S'il n'y a aucune restriction en a) j'aimerais connaître ton raisonnement pour déduire qu'il y a 6! possibilités.
Consulte ce site:
Question
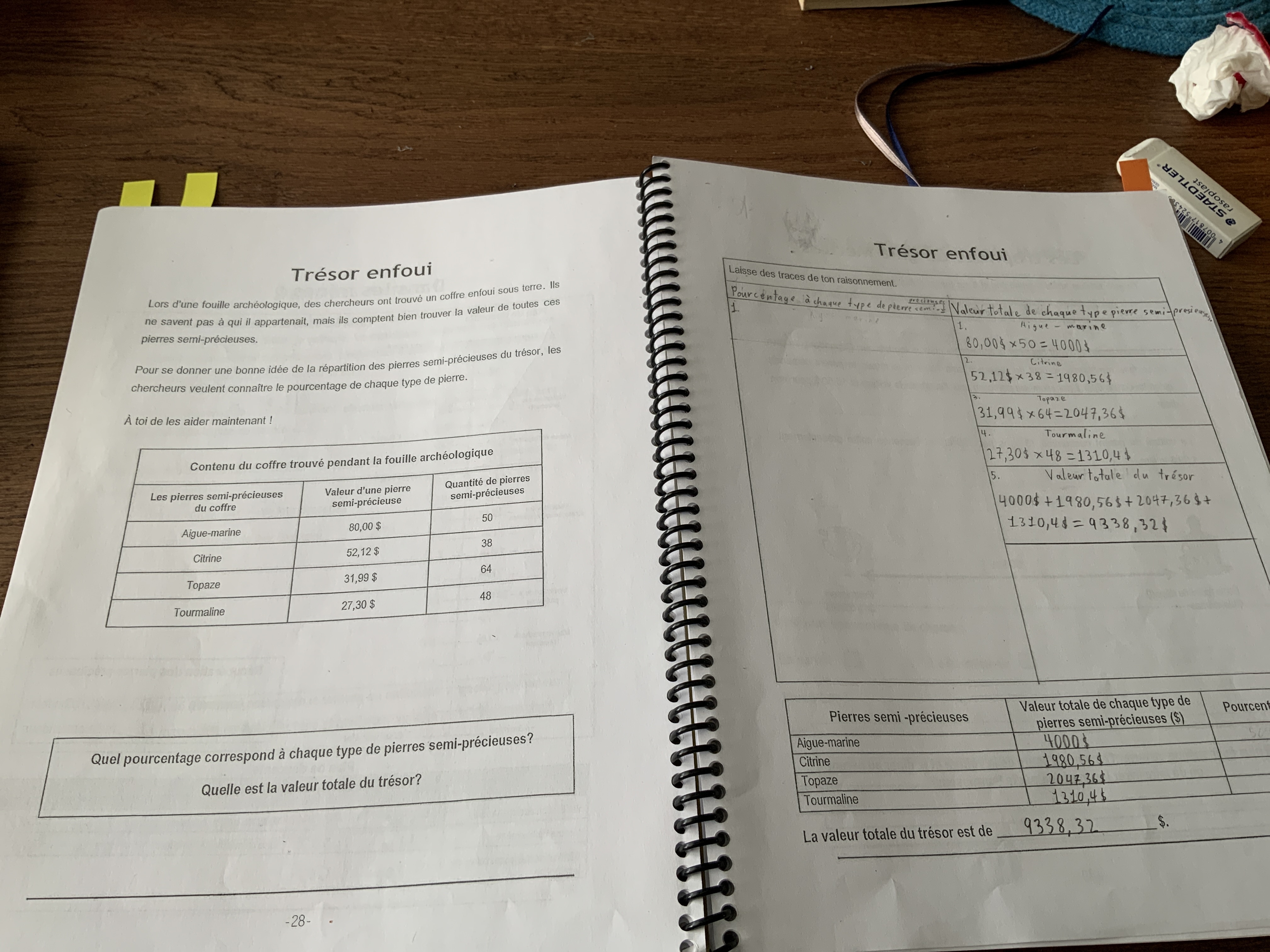
Bonjour alloprof est-ce que vous pouvez m’ aider avec le problème de math dans la partie des pourcentages?Merci !😀
Re : Question
Bonjour Ara Enthousiaste!
Merci de faire appel à nos services!
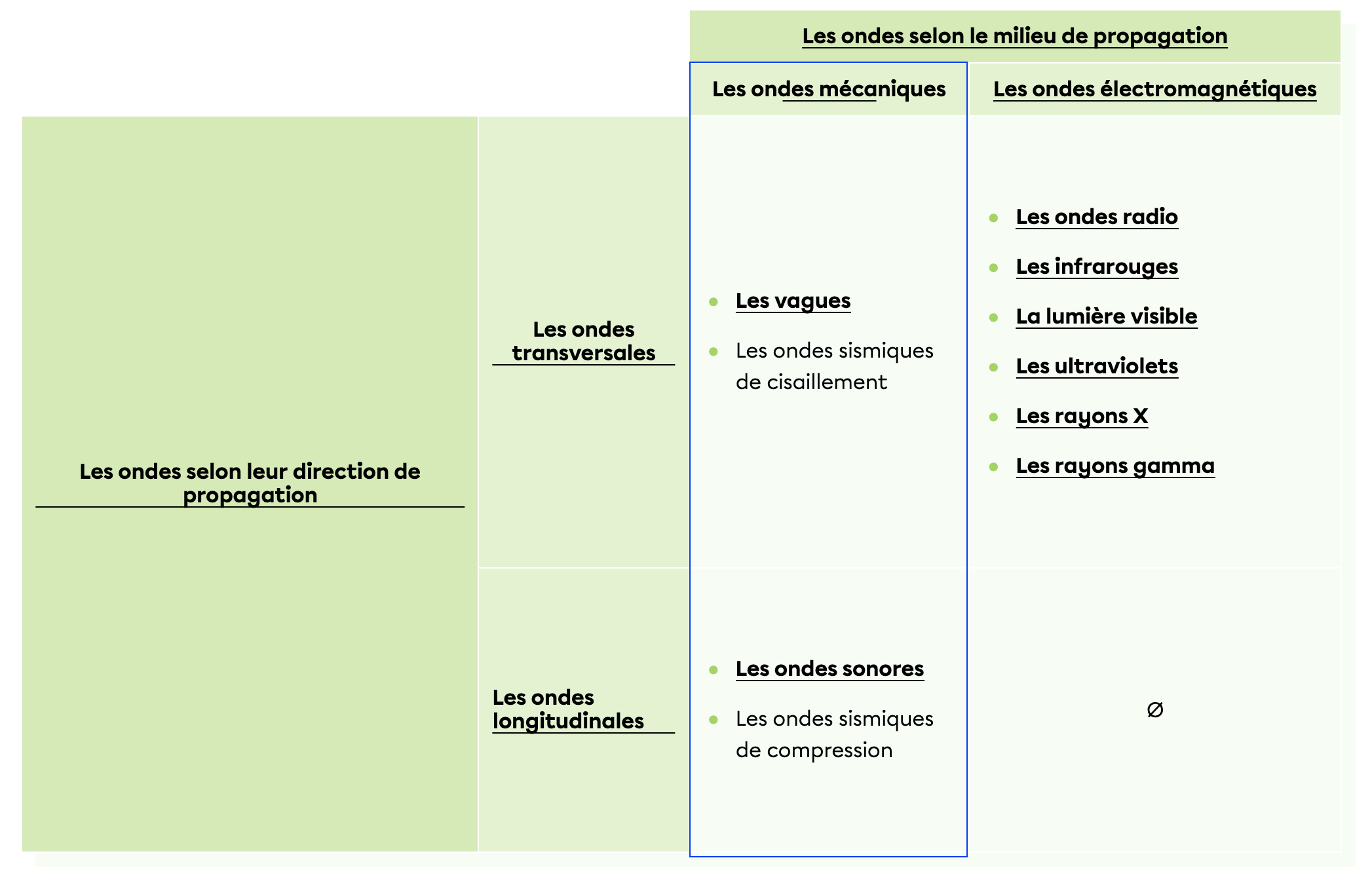
Dans un premier temps, les ondes mécaniques ne désignent pas seulement des ondes sous forme de vague.
Les ondes mécaniques sont celles qui se propagent pas le déplacement de particules. Ceci peut comprendre les vagues, soit des ondes transversales, mais aussi les ondes sonores qui sont longitudinales.
Tu peux observer les ondes comprises dans les ondes mécaniques dans le tableau suivant:
À la deuxième image, ceci représente réellement la manière dont le son se propage, soit par zones de compression et de raréfaction.
Pour en apprendre davantage sur les ondes sonores, tu peux consulter la fiche explicative suivante:
J'espère que cela t'aidera!
Re : Question
Salut!
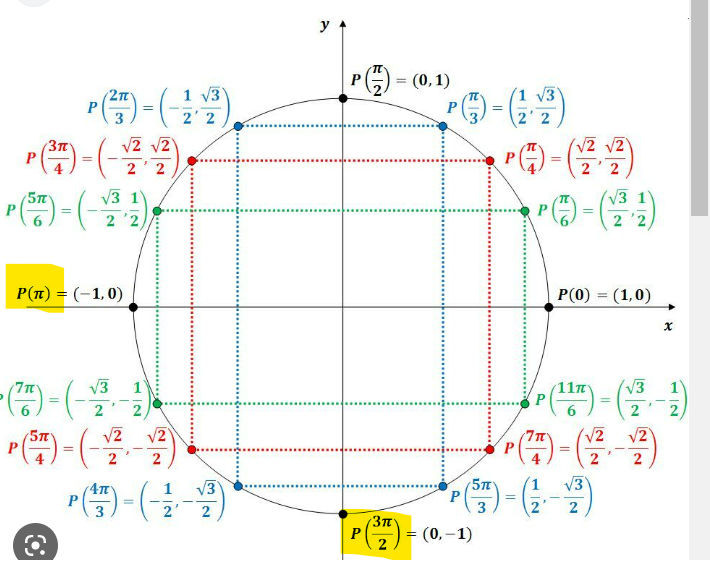
Tu dois te servir du cercle trigonométrique et de l'intervalle de l'angle x donné.
On te dit que l'angle x est dans l'intervalle [\(\pi, \frac{3\pi}{2}\)]. Donc, on peut déduire qu'on doit se situer dans le 3e quadrant :
Puisqu'on est dans le 3e quadrant, on a donc des coordonnées en x et en y négatives. Ainsi, le cosinus et le sinus de l'angle doivent donner des résultats négatifs.
Si nous nous étions situés dans le second quadrant, alors seul le cosinus devrait être négatif (la coordonnée en x est négative et la coordonnée en y est positive).
À l'inverse, si on était dans le quatrième quadrant, le cosinus serait positif et le sinus négatif (x positif et y négatif).
Finalement, si nous étions dans le premier quadrant, le sinus et le cosinus devraient être positifs.
J'espère que c'est plus clair pour toi! :)
Re : Question
Salut!
Pour le second numéro, tu as fait une petite erreur dans ton calcul pour le spectacle Pop. Tu as oublié d'ajouter le 1h lorsque tu as soustrait 60 de 90, tu as seulement ajouté le 30 minutes. Ainsi, il devrait être 22h25 et non 21h25 90 minutes après 20h55. Tu devras alors changer tes réponses pour les spectacles suivant le spectacle Pop.
De plus, n'oublie pas que les deux amis doivent être rentrés pour 22h, ils ne peuvent donc pas quitter le festival à 22h35. Tu dois également prendre en compte le temps nécessaire pour retourner chez eux.
Je te laisse corriger ces erreurs. Si tu as d'autres questions, n'hésite pas à nous réécrire! :)