Constructing a Trapezoid

A trapezoid is a quadrilateral that has one pair of parallel sides named "small base" and "large base" due to their different lengths.

1. Using a ruler, draw a line segment that corresponds to the length of the large base.

2. Place the set square anywhere on the large base and draw a perpendicular line segment longer than the trapezoid’s height.

3. Using the ruler, mark the spot on the perpendicular line that corresponds to the trapezoid’s height.

4. Place the set square on that mark and draw a line that extends from it.

5. Use the ruler to make sure the line drawn in step 4 is the length of the small base.

6. Using the ruler, connect the ends of each base.

Draw a trapezoid with a large base of |7\:\text{cm}|, a small base of |4\:\text{cm}| and a height of |3\:\text{cm}|.

Using a ruler, draw a line segment that corresponds to the length of the large base (7 cm).	Place the set square anywhere on the large base and draw a perpendicular line segment longer than the height (3 cm).
Using the ruler, mark the spot on the perpendicular line segment that corresponds to the trapezoid’s height (3 cm).	Place the set square on that mark and draw a line that extends from it.
Use the ruler to make sure that the line drawn in step 4 is the length of the small base (4 cm). ​	Using the ruler, connect the ends of each of the bases.

1. Using a ruler, draw a line segment that corresponds to the length of the large base.

2. Place the protractor at one end of the large base and draw an angle according to the specified measurement.

3. Using the ruler, extend the angle line so that it is the same length as the trapezoid’s oblique side.

4. Repeat steps 2 and 3 on the other end of the large base, making sure the angle and oblique line correspond to the specified measurements.

5. Using the ruler, connect the ends of the two oblique line segments.

Draw a trapezoid with bases measuring |5\:\text{cm}| and |2.5\:\text{cm}|, as well as oblique sides measuring |2.5\:\text{cm}| and |3\:\text{cm}|. Finally, the measurements of the acute angles formed by the oblique sides and the large base are |70^o| and |51^o|, respectively.

Using a ruler, draw a line segment that corresponds to the length of the large base (5 cm).	Place the protractor at one end of the large base and draw the first angle (70o).
Using the ruler, extend the angle line so that it is the same length as the oblique side (2.5 cm).	Repeat steps 2 and 3 on the other end of the large base, making sure the angle and oblique line correspond to the measurements given.
Using the ruler, connect the ends of the two oblique line segments.

​

An isosceles trapezoid is a quadrilateral with a pair of congruent sides. It also has another pair of parallel opposite sides named the "small base" and "large base" due to their different lengths.

1. Using a ruler, draw a line segment that corresponds to the length of the large base.

2. Place the set square on one end of the large base and draw a perpendicular line segment longer than the trapezoid’s height.

3. Using the ruler, mark the spot on the perpendicular line that corresponds to the trapezoid’s height.

4. Repeat steps 2 and 3 on the other end of the large base.

5. Using the ruler, join the two marks that represent the trapezoid’s height.

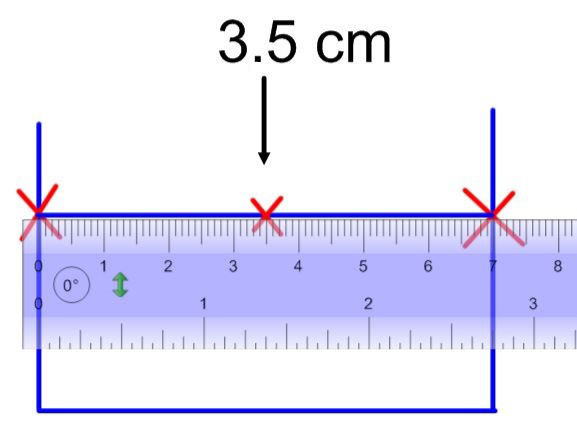
6. Using the ruler, locate and mark the midpoint of the line segment drawn in step 5.

7. Using the ruler, measure half the length of the small base. Mark this distance on either side of the midpoint found in step 6

8. Join the ends of the large base to the marks made in step 7.

Draw an isosceles trapezoid with a large base measuring |7\:\text{cm}|, a small base measuring |4\:\text{cm}|, and a height equal to |3\:\text{cm}|.

Using a ruler, draw a line segment that corresponds to the length of the large base (7 cm).	Place the set square on one end of the large base and draw a perpendicular line segment longer than 3 cm.
Using the ruler, mark the spot on the perpendicular line that corresponds to the trapezoid’s height (3 cm).	Repeat steps 2 and 3 on the other end of the large base.
Using the ruler, join the two marks that represent the trapezoid’s height.	Using the ruler, locate the midpoint of the line segment (3.5 cm).
Using the ruler, measure half the length of the small base (2 cm) and mark this distance on both sides of the midpoint.	Join the ends of the large base to the marks made in step 7.

1. Using a ruler, draw a line segment that corresponds to the length of the large base.

2. Place the protractor at one end of the large base and draw the angle according to the specified measurement.

3. Using the ruler, extend the angle’s line to equal the length of the trapezoid’s oblique side.

4. Repeat steps 2 and 3 on the other end of the large base.

5. Using the ruler, connect the endpoints of the two oblique segments.

Draw an isosceles trapezoid with a large base measuring |10\:\text{cm}|, oblique sides measuring |4\:\text{cm}|, and acute angles measuring |45^o|.

Using the ruler, draw a line segment that corresponds to the length of the large base (10 cm).	Place the protractor at one end of the segment and draw a 45o angle.
Using the ruler, extend the angle's line to equal the length of the oblique side of 4 cm.	Repeat steps 2 and 3 on the other end of the large base.
Using the ruler, connect the endpoints of the two oblique segments. ​

A right trapezoid has two consecutive right angles and a pair of opposing parallel sides named the "small base" and "large base" because of their different lengths.

1. Using a ruler, draw a line segment that corresponds to the length of the large base.

2. Place the set square at one end of the large base and draw a perpendicular line segment longer than the trapezoid’s height.

3. Using the ruler, mark the spot on the perpendicular line segment that corresponds to the trapezoid’s height.

4. Place the set square on the height of the trapezoid where the line of the small base will go.

5. Use the ruler to draw the line that is the length of the small base (4 cm).

6. Using the ruler, join the ends of each base.

Draw a rectangle trapezoid with the large base measuring |7\:\text{cm}|, the small base measuring |4\:\text{cm}|, and a height equal to |3\:\text{cm}|.

Using a ruler, draw a line segment that corresponds to the length of the large base (7 cm).	Place the set square at one end of the large base and draw a perpendicular line segment that is longer than the height.
Using the ruler, mark the spot on the perpendicular line segment that corresponds to the trapezoid’s height (3 cm).	Place the set square on the height of the trapezoid where the line of the small base will go.
With the ruler, draw a line segment corresponding to the length of the small base.	Using the ruler, join the ends of each base.

1. Using a ruler, draw a line segment that corresponds to the length of the large.

2. Place the protractor at one end of the large base and draw the 90^o angle.

3. Using the ruler, extend the angle’s line so that it is the length of the trapezoid’s height.

4. Repeat steps 2 and 3 on the other end of the height.

5. Using the ruler, join the endpoints of the two bases.

Draw a right trapezoid with bases measuring |6\:\text{cm}| and |4\:\text{cm}| and the height measuring |3\:\text{cm}|.

Using a ruler, draw a line segment that corresponds to the length of the large base (6 cm).	Place the protractor at the one end of the large base and draw the 90o angle.
Using the ruler, extend the angle’s line so that it is the length of the trapezoid’s height (3 cm).	Repeat steps 2 and 3 on the other end of the height.
Join the endpoints of the two bases using the ruler.