Subjects
Grades
Finding the Rule of a Cosine Function
Concept sheet | Mathematics
Secondary
5
Table of contents
The rule of a cosine function is |f(x)=a\cos\!\big(b(x-h)\big)+k.|
Parameter |a| is related to the amplitude.
Parameter |b| is related to the period.
Parameter |h| is related to the phase shift.
Parameter |k| is related to the axis of oscillation.
When looking for the rule of a sinusoidal function using the cosine function, we need to locate a cycle that begins at an extreme point (a maximum or a minimum) and ends at the same height. The point at the start of the chosen cycle corresponds to point |(h,k+A)| if it is a maximum and to point |(h,k-A)| if it is a minimum.
Since there are an infinite number of extremes for the same cosine function, there are an infinite number of possible values for |h| and |k.|
-
Determine |k| using the axis of oscillation.
-
Choose an extreme and determine |h.|
-
Determine one cycle starting from the chosen extreme.
-
Determine |\vert a\vert| from the amplitude.
-
Determine |b| from the period.
-
Determine the sign of |a.|
If the function begins at a maximum, |a| is positive.
If the function begins at a minimum, |a| is negative. -
Write the rule of the function.
Determine the rule of the cosine function that passes through points |(1.25,-0.25)| and |(2.75,-1.75)| which respectively represent maximum and minimum points.
See solution
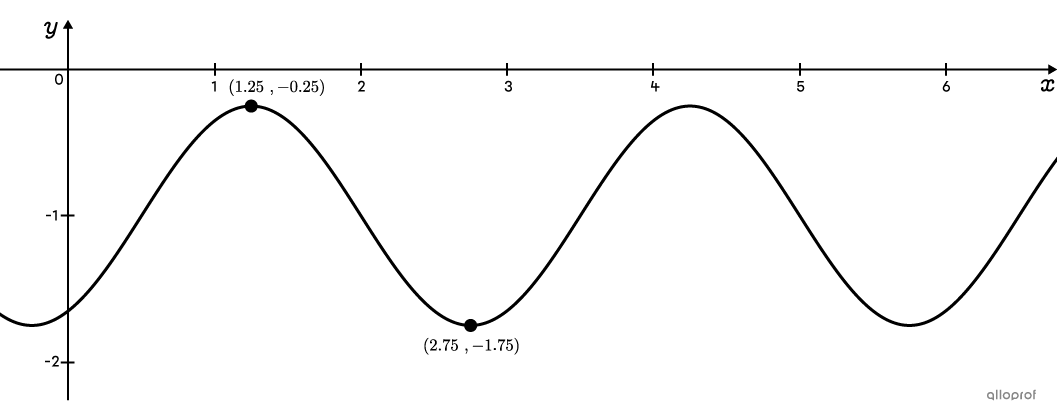
In the last example, by choosing the maximum point |(1.25, -0.25),| the following rule was obtained:||f(x)=0.75\cos\left(\dfrac{2\pi}{3}(x-1.25)\right)-1||
If, instead, point |(2.75, -1.75)| had been chosen, the function would have started at a minimum, which means that |a| would have been negative. The following rule would then have been obtained:||f(x)=-0.75\cos\left(\dfrac{2\pi}{3}(x-2.75)\right)-1||An analysis of these rules shows that the values of |\vert a\vert,| |b| and |k| never change. The only differences between the rules are the value of |h| and the sign of |a.|
Here is an example where the complete cycle is not shown on the Cartesian plane.
Determine the rule of the cosine function that passes through points |\left(-\dfrac{4\pi}{3},0\right)| and |\left(-\dfrac{\pi}{3},4\right)| which respectively represent a minimum and a maximum.
See solution
Here is an example where the vertices are not directly provided. This requires a little more calculation to determine the parameters.
Determine the rule of the cosine function that passes through points |\left(-\dfrac{3}{4},-2\right)| and |\left(\dfrac{5}{4},-2\right).|
See solution
When the inflection points of a sinusoidal function are given, it is best to find the rule of a sine function. That way, there are fewer calculations.
When asked to find the equation of a sinusoidal function, it's possible to use the equation of a sine function or a cosine function. Here is an example of how to find the equation of a cosine function using trigonometric identities.
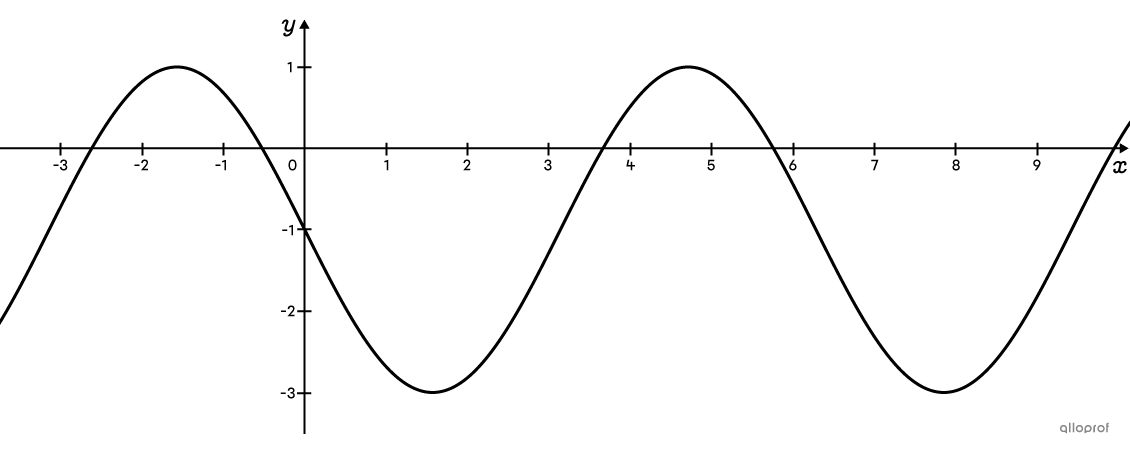
Here is a sinusoidal function whose rule, based on the sine function, is |f(x)=-2\sin(x)-1.|
To transform the equation into a cosine function, apply the following trigonometric identity:
|\sin(x)=\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right).|||\begin{align}f(x)&=-2\sin(x)-1\\ f(x)&=-2\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right)-1\end{align}||The 2 previous rules are equivalent.
Note: Although the rule changed from a sine function to a cosine function, |\vert a \vert| and |\vert b\vert| did not change, since the amplitude and the period remained the same. Notice that |k| did not change either, since the axis of oscillation is also the same.
The only possible differences between the rules are the value of |h,| and the signs of |a| and |b.|