Solving a Tangent Equation or Inequality

A tangent equation or inequality contains a tangent ratio, where the unknown |(x)| is found in the argument.

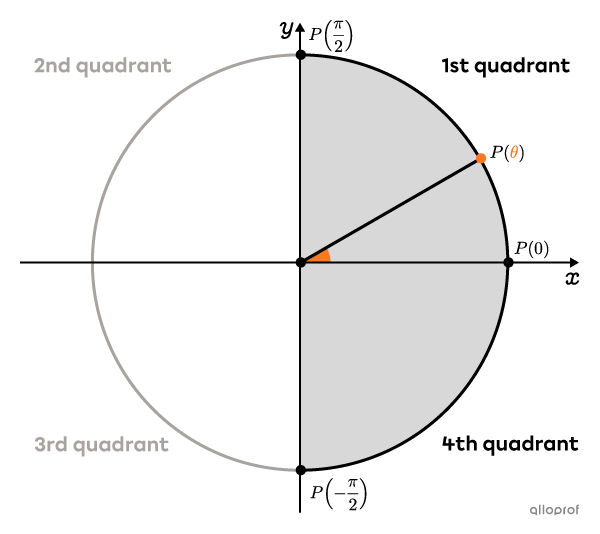
The inverse function |\arctan| is sometimes denoted |\tan^{-1},| especially on calculators.

There are some main values for the tangent ratio, which can be used when solving a tangent equation or inequality.

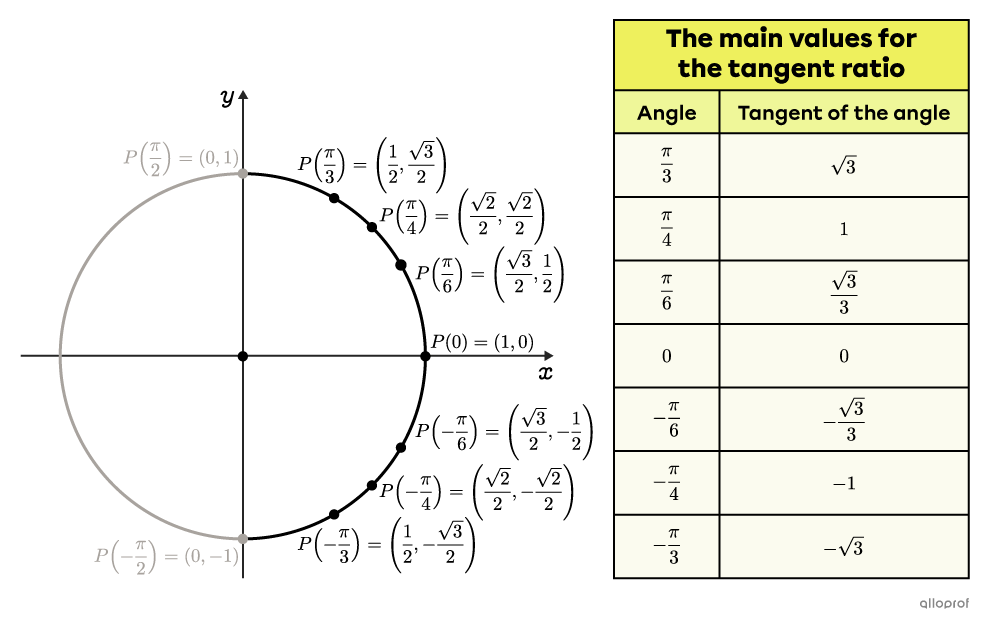
These values are obtained by dividing the |y| and |x| coordinates of the main points located in the 1st and 4th quadrants of the unit circle. Here's an example of the calculation using the angle |-\dfrac{\pi}{6}.| ||\begin{align}\tan\left(-\dfrac{\pi}{6}\right)&=\dfrac{\sin\left(-\dfrac{\pi}{6}\right)}{\cos\left(-\dfrac{\pi}{6}\right)}\\[3pt]&=\dfrac{-\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}}\\[3pt]&=-\dfrac{1}{\color{#ec0000}{\cancel{\color{black}{2}}}}\times\dfrac{\color{#ec0000}{\cancel{\color{black}{2}}}}{\sqrt{3}}\\[3pt]&=-\dfrac{1}{\sqrt{3}}\boldsymbol{\color{#ec0000}{\times\dfrac{\sqrt{3}}{\sqrt{3}}}}\\[3pt]&=-\dfrac{\sqrt{3}}{3}\end{align}||Note: There is no main value for the angles |\dfrac{\pi}{2}| and |-\dfrac{\pi}{2},| since we get a division by |0.| For this reason, the basic |\tan(x)| function has asymptotes at |x=\dfrac{\pi}{2}| and |x=-\dfrac{\pi}{2}.|

1. Isolate the tangent ratio.

2. Determine the trigonometric angle using the table of main values or the inverse function |\boldsymbol{\arctan}.|

3. Solve the equation obtained with the trigonometric angle.

4. Calculate the period of the tangent function.

5. Give the solutions of the equation.

Solve the following equation:||\tan(2x)-3=-2||

Solve the following equation for the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||5\tan\big(\!-4(x+1)\big)+2=6||

Solve the following equation:||2\tan^2(x-2)-5\tan(x-2)+2=0||

1. Change the inequality symbol to an equal symbol.

2. Isolate the tangent ratio.

3. Determine the trigonometric angle using the table of main values or the inverse function |\boldsymbol{\arctan}.|

4. Solve the equations obtained with the trigonometric angles.

5. Calculate the period of the tangent function.

6. Calculate the asymptotes of the tangent function.

7. Give the solution set of the inequality.

Solve the following inequality:||3\tan\left(\dfrac{x}{4}\right)>-\sqrt{3}||

Solve the following inequality:||\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5||

Solve the following inequality:||\tan^2\left(\dfrac{2x}{3}\right)\ge\dfrac{16}{9}||