Subjects
Grades
Thales’ Theorem
Concept sheet | Mathematics
Secondary
4
Thales' theorem is very useful when finding one or more missing measurements in a figure formed by intersecting transversals that cross parallel lines.
If, in a figure…
-
lines |\color{#3a9a38}{BD}| and |\color{#3b87cd}{CE}| are transversals that intersect at |A,|
-
lines |\color{#ec0000}{BC}| and |\color{#ec0000}{DE}| are parallel,
then the following proportion exists:
||\color{#3a9a38}{\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}}=\color{#3b87cd}{\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}}= \color{#ec0000}{\dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}}||
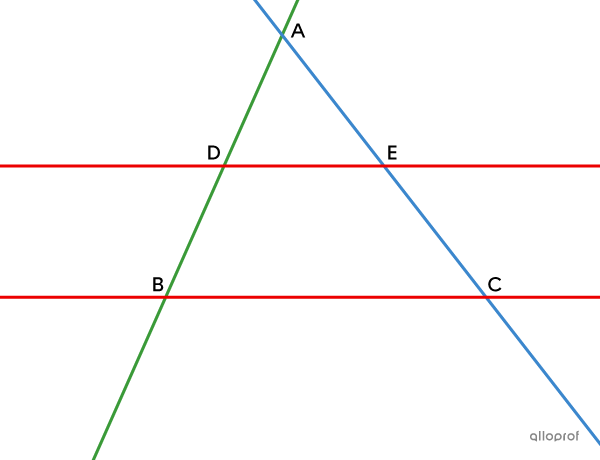
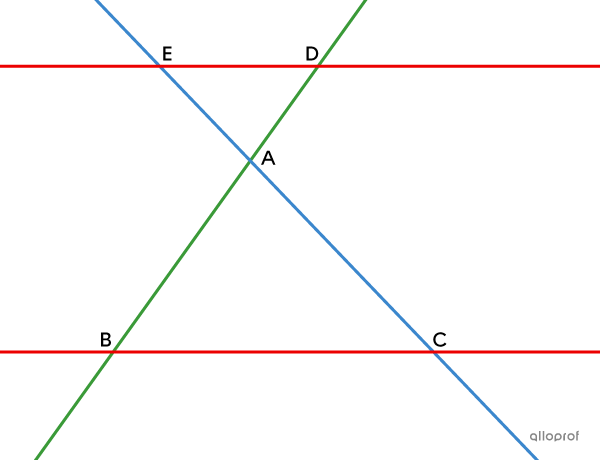
Note: Thales' theorem applies regardless of whether the transversals |(\color{#3b87cd}{EC}| and |\color{#3a9a38}{BD})| intersect inside or outside the parallel lines |\color{#ec0000}{ED}| and |\color{#ec0000}{BC}).|
Proof of Thales’ Theorem
Thales' theorem is based on the proportions of corresponding sides in similar triangles. It is proven by showing that |\triangle ABC \sim \triangle ADE| using the minimum condition for similarity AA.
Hypothesis
Consider distinct parallel lines |\color{#ec0000}{BC}| and |\color{#ec0000}{DE},| as well as intersecting transversals |\color{#3a9a38}{AB}| and |\color{#3b87cd}{AC}.|
Conclusion
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}} = \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}} = \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}||
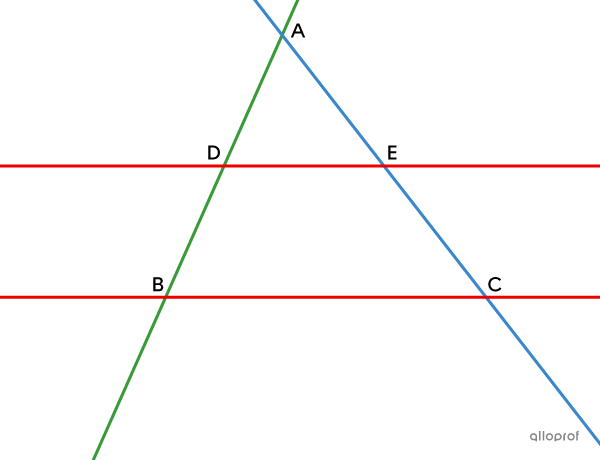
Proof
| Statement | Justification | ||
|---|---|---|---|
|
1 |
Angles |DAE| and |BAC| are congruent.||\angle DAE\cong\angle BAC|| |
A |
It is an angle common to both triangles. |
|
2 |
Angles |ADE| and |ABC| are congruent.||\angle ADE\cong\angle ABC|| |
A |
Corresponding angles formed by parallel lines |(\color{#ec0000}{BC}| and |\color{#ec0000}{DE})|, cut by a transversal |(\color{#3a9a38}{AB})| are congruent. |
|
3 |
Triangles |ABC| and |ADE| are similar.||\triangle ABC\sim\triangle ADE|| |
They satisfy the minimum condition AA: two triangles are similar if they have 2 pairs of corresponding congruent angles. |
|
|
4 |
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}} = \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}} = \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}|| |
The corresponding sides of similar triangles are proportional. |
|
The proof of Thales' theorem when the intersection point |(A)| of the transversals is situated inside the 2 parallel lines is also established using the minimum condition of similarity AA.
Finding Missing Measurements Using Thales’ Theorem
Once we know that there are 2 parallel lines cut by 2 intersecting transversals, we can use Thales' theorem to solve the proportion in the triangles without having to prove that they are similar.
Find the missing measurement, given that lines |\color{#ec0000}{ED}| and |\color{#ec0000}{BC}| are parallel.
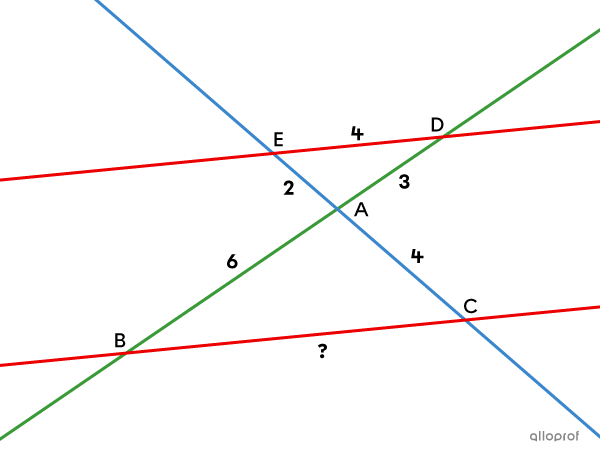
According to Thales’ theorem, since lines |\color{#ec0000}{ED}| and |\color{#ec0000}{BC}| are parallel, the following proportion exists:
||\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}= \dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}= \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}||
To find |\text{m}\overline{BC},| we can solve the following equation:
||\begin{align}\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}&= \dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}\\ \dfrac{2}{4}&=\dfrac{4}{\text{m}\overline{BC}}\\\\ \text{m}\overline{BC}&=\dfrac{4\times 4}{2}\\&=8\end{align}||
Answer: |\text{m}\overline{BC} = 8\ \text{units}|
The Converse of Thales’ Theorem
In the situations associated with Thales' theorem, if the lines are parallel, then a proportion can be derived. However, it is also possible to apply the opposite reasoning, in other words, if the proportion is valid, then we can conclude that the lines are parallel. This is called the converse of Thales' theorem.
Given that transversal lines |\color{#3b87cd}{EC}| and |\color{#3a9a38}{BD}| intersect at |A,| prove that lines |\color{#ec0000}{ED}| and |\color{#ec0000}{BC}| are parallel.
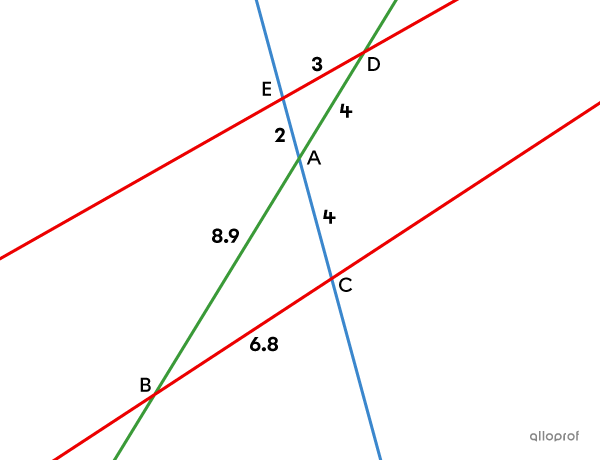
We must verify if the proportion of Thales' theorem between the corresponding sides of the triangles |ADE| and |ABC| is true. If we show that the 3 ratios are equivalent, then we can conclude that the lines are parallel.
||\begin{align}\color{#3a9a38}{\dfrac{\text{m}\overline{AD}}{\text{m}\overline{AB}}}&=\color{#3b87cd}{\dfrac{\text{m}\overline{AE}}{\text{m}\overline{AC}}}= \color{#ec0000}{\dfrac{\text{m}\overline{DE}}{\text{m}\overline{BC}}}\\ \color{#3a9a38}{\dfrac{4}{8.9}}\quad &\neq\quad\color{#3b87cd}{\dfrac{2}{4}}\quad \neq\quad\color{#ec0000}{\dfrac{3}{6.8}}\end{align}||
Conclusion: Since the 3 ratios are not equal, lines |\color{#ec0000}{ED}| and |\color{#ec0000}{BC}| are not parallel.
Generalization of Thales’ Theorem
When we have several parallel lines intersected by 2 transversals, it is possible to use the generalized Thales' theorem.
Given that, in a figure:
-
lines |\color{#ec0000}{AA’},| |\color{#ec0000}{BB’}| and |\color{#ec0000}{CC’}| are parallel
-
points |A,| |B| and |C| are aligned
-
points |A’,| |B’| and |C’| are aligned
then the following proportion exists:
||\dfrac{\color{#3b87cd}{\text{m}\overline{A’B’}}}{\color{#3a9a38}{\text{m}\overline{AB}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{B’C’}}}{\color{#3a9a38}{\text{m}\overline{BC}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{A’C’}}}{\color{#3a9a38}{\text{m}\overline{AC}}}||
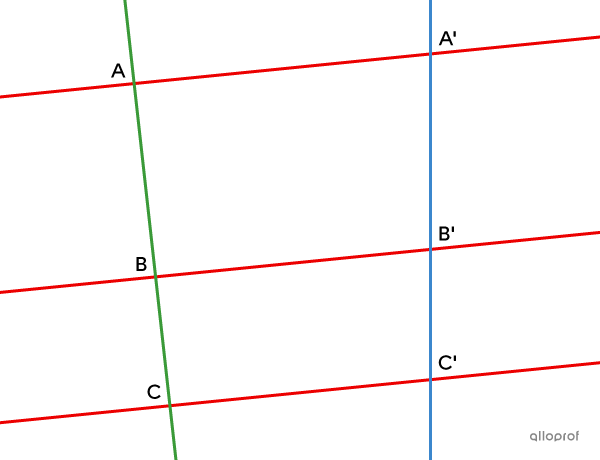
In the generalized Thales' theorem, we cannot establish a proportion between the segments located on the parallel lines |(AA’,| |BB’| and |CC’).|
||\dfrac{\text{m}\overline{AA’}}{\text{m}\overline{BB'}}\boldsymbol{\color{#ec0000}\neq} \dfrac{\text{m}\overline{BB’}}{\text{m}\overline{CC'}}\boldsymbol{\color{#ec0000}\neq} \dfrac{\text{m}\overline{AA’}}{\text{m}\overline{CC'}}||
Given that lines |\color{#ec0000}{AA’},| |\color{#ec0000}{BB’}| and |\color{#ec0000}{CC’}| are parallel, find |\text{m}\overline{B'C'}.|
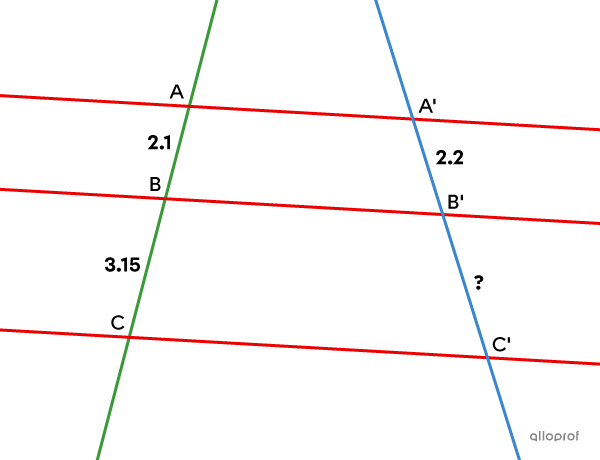
According to the generalized Thales’ theorem, since the lines |\color{#ec0000}{AA’},| |\color{#ec0000}{BB’}| and |\color{#ec0000}{CC’}| are parallel, the following proportion can be applied: ||\dfrac{\color{#3b87cd}{\text{m}\overline{A’B’}}}{\color{#3a9a38}{\text{m}\overline{AB}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{B’C’}}}{\color{#3a9a38}{\text{m}\overline{BC}}} = \dfrac{\color{#3b87cd}{\text{m}\overline{A’C’}}}{\color{#3a9a38}{\text{m}\overline{AC}}}||
To find |\text{m}\overline{B’C’},| we solve the following equation:
||\begin{align}\dfrac{\color{#3b87cd}{\text{m}\overline{A'B'}}}{\color{#3a9a38}{\text{m}\overline{AB}}}&= \dfrac{\color{#3b87cd}{\text{m}\overline{B'C'}}}{\color{#3a9a38}{\text{m}\overline{BC}}}\\ \dfrac{\color{#3b87cd}{2.2}}{\color{#3a9a38}{2.1}}&= \dfrac{\color{#3b87cd}{x}}{\color{#3a9a38}{3.15}}\\\\ x&=\dfrac{3.15\times 2.2}{2.1}\\&=3.3\end{align}||
Answer: |\text{m}\overline{B’C’}=3.3\ \text{units}|