The Area of Truncated Solids

A truncated solid is a solid that has been cut by a plane where only a portion of the original figure remains. The plane cutting the solid may be parallel to its base or not.

The following is an illustration of various cones truncated by a plane.

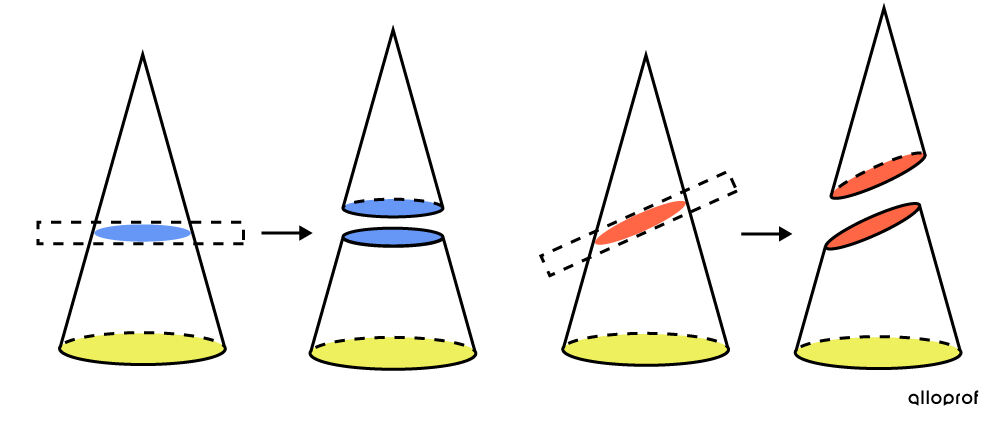
In the image, we see that the first two cones are created using a plane parallel to the base of the cone. This type of truncated cone will be studied here. 

In the case of the last two cones, the plane is not parallel to the base of the cone. This type of truncated cone will not be studied here. 

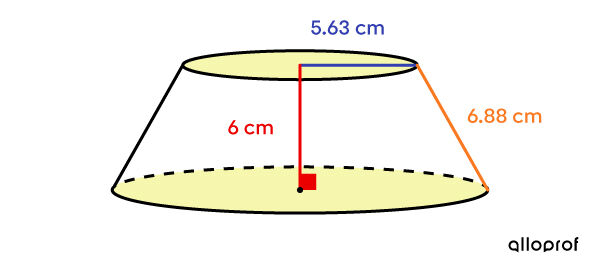
What is the total area of the following truncated cone given that the radius, height and apothem of the original cone associated with it measure 9 cm, 16 cm and 18.36 cm respectively?

1. Calculate the area of the bases
   In this case, the bases are two circles which have different radius measurements.

||\begin{align} A_\text{small base} &= \pi \color{#333FB1}{r}^2 \\ &= \pi (\color{#333FB1}{5.63})^2 \\ &\approx 99.58\ \text{cm}^2 \end{align}||

||\begin{align} A_\text{large base} &= \pi \color{#333FB1}{r}^2\\ &= \pi (\color{#333FB1}{9})^2 \\ &\approx 254.47\ \text{cm}^2 \end{align}||

||\begin{align} A_\text{bases} &= 99.58 + 254.47 \\ &= 354.05\ \text{cm}^2 \end{align}||

2. Identify the associated solids
   To help with the rest of the calculations, it is essential to correctly identify the initial known solids. In this case, cones were used to create the solid.

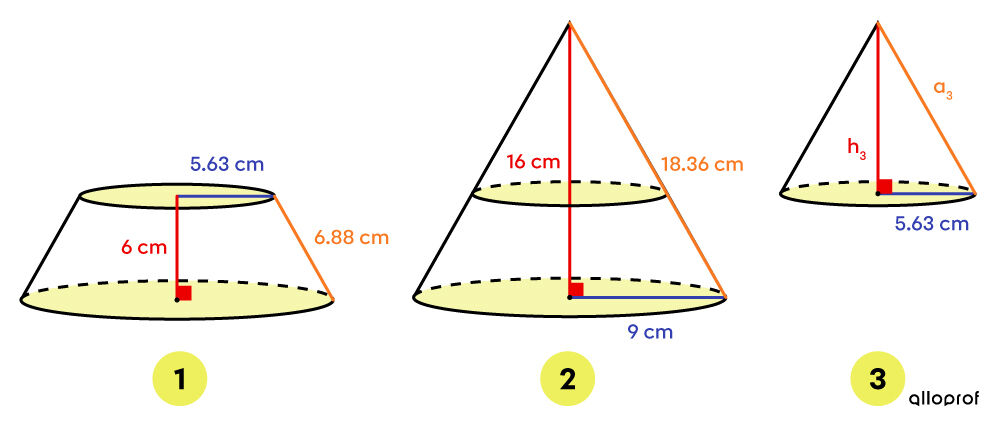
3. Calculate the lateral area
   The measure of the apothem of the truncated portion (figure 3) must be found. We can use subtraction to find it.||\begin{align} a_3 &= a_2 - a_1 \\ &= 18.36 - 6.88 \\ &= 11.48 \ \text{cm} \end{align}||Referring to the solids found in the other steps, we can determine the following. ||\begin{align} A_{L1} &= A_{L2} - A_{L3}\\ &= \pi r_2 a_2 - \pi r_3 a_3 \\ &= \pi (9) (18.36) - \pi (5.63) (11.48) \\ &\approx 316.07 \ \text{cm}^2 \end{align}||

4. Calculate the total area
   ||\begin{align} A_T &= A_L + A_\text{bases}\\ &\approx 316.07 +354.05\\ &\approx 670.12 \ \text{cm}^2 \end{align}||​

5. Interpret the answer
   The total area of the truncated cone is approximately |670.12\ \text{cm}^2.|

Ariane wants to wrap a gift that she bought for her little sister. The box, illustrated below, has the form of a truncated pyramid.

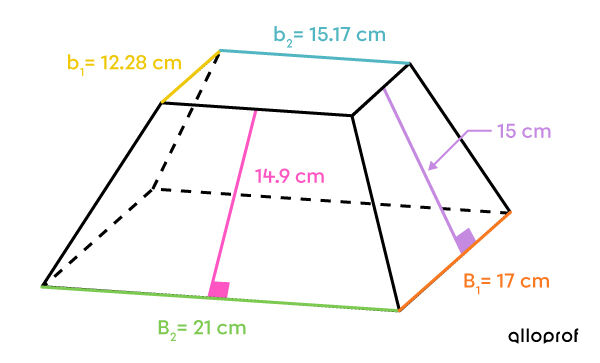
What is the minimum surface area of wrapping paper that Ariane will need to wrap the present?

1. Calculate the area of the bases
   The two bases are rectangles with different measurements.

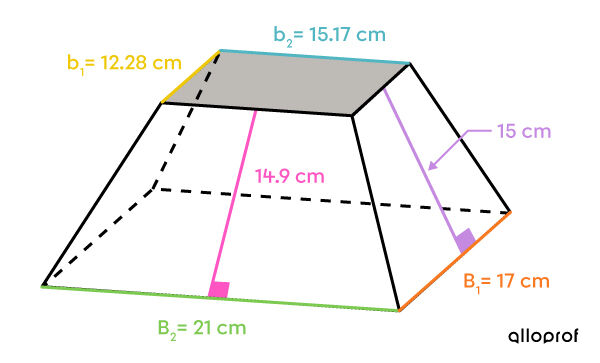
||\begin{align} A_\text{small base} &= \color{#51b6c2}{b} \times \color{#efc807}{h} \\ &= \color{#51b6c2}{15.17} \times \color{#efc807}{12.28} \\ &\approx 186.29\ \text{cm}^2 \end{align}||

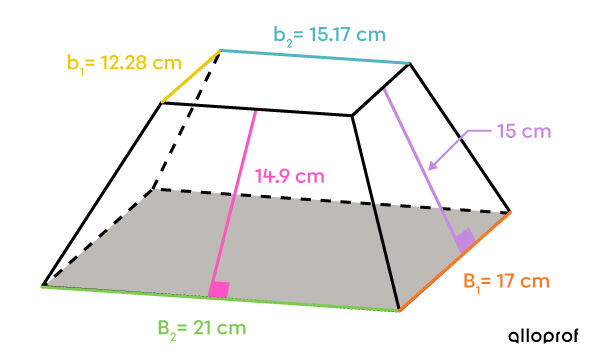
||\begin{align} A_\text{large base} &= \color{#7cca51}{b} \times \color{#fa7921}{h} \\ &= \color{#7cca51}{21} \times \color{#fa7921}{17} \\ &= 357\ \text{cm}^2 \end{align}||

||\begin{align} A_\text{bases} &= 186.29 + 357 \\ &= 543.29\ \text{cm}^2 \end{align}||

2. Calculate the lateral area 
   The lateral area is made up of 2 pairs of isosceles trapezoids.

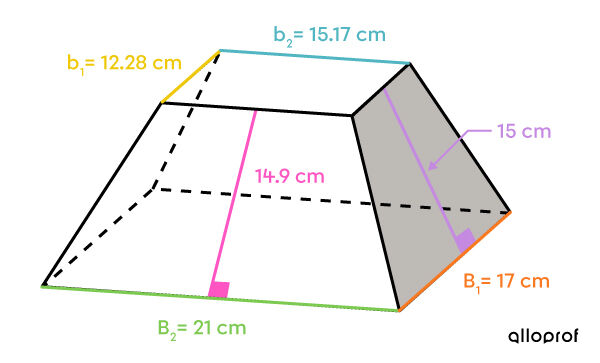
||\begin{align}A_\text{small trapezoid} &= \dfrac{(\color{#fa7921}{B_1}+ \color{#efc807}{b_1}) \times \color{#c58ae1}{h}}{2}\\ &=\dfrac{(\color{#fa7921}{17}+ \color{#efc807}{12.28}) \times \color{#c58ae1}{15}}{2}\\ &= 219.6\ \text{cm}^2\end{align}||

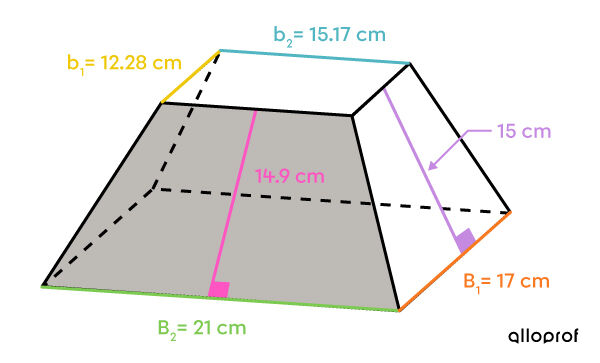
||\begin{align}A_\text{large trapezoid} &= \dfrac{(\color{#7cca51}{B_2}+ \color{#51b6c2}{b_2}) \times \color{#ff55c3}{h}}{2}\\ &=\dfrac{{(\color{#7cca51}{21}+ \color{#51b6c2}{15.17})} \times \color{#ff55c3}{14.9}}{2}\\ &\approx{269.47}\ \text{cm}^2\end{align}||

||\begin{align} A_\text{L} &= {2}\times{A_\text{small trapezoid}} +{2}\times{A_\text{large trapezoid}}  \\ &= {2}\times{219.6} +{2}\times{269.47}\\&= 978.14\ \text{cm}^2 \end{align}||

3. Calculate the total area
   ||\begin{align} A_T &= A_\text{bases} + A_L\\ &= 543.29 +978.14\\ &= 1\ 521.43 \ \text{cm}^2 \end{align}||​

4. Interpret the answer
   Ariane will need at least |1\ 521.43\ \text{cm}^2| of wrapping paper to wrap the present for her little sister.