Subjects
Grades
The Area and the Volume of Solids
Concept sheet | Mathematics
Secondary
2-3
Area of a Solid
We refer to area calculations when trying to cover a solid or a surface. There are 3 types of areas to differentiate between solids.
The area of the base, generally denoted |A_b,| is the surface occupied by the figure or figures that serve as base for the solids.
The lateral area, generally denoted |A_L,| is the surface occupied by the figures which do not serve as base for the solids.
The total area, generally denoted |A_T,| is the total surface covered by all the figures that make up the solid.
To know which area to use, refer to the context or carefully read the problem’s instructions.
The Lateral Area
To repair a pool, we want to replace the wall around it.
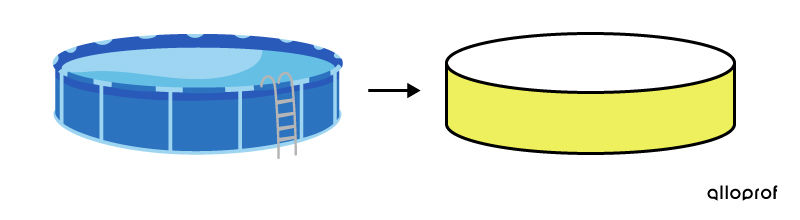
In this context, the wall refers to the lateral face of the cylinder surrounding the pool. Thus, the lateral area is the focus.
The Area of the Base
For a cone-shaped teepee, we want to buy a carpet to cover the floor.
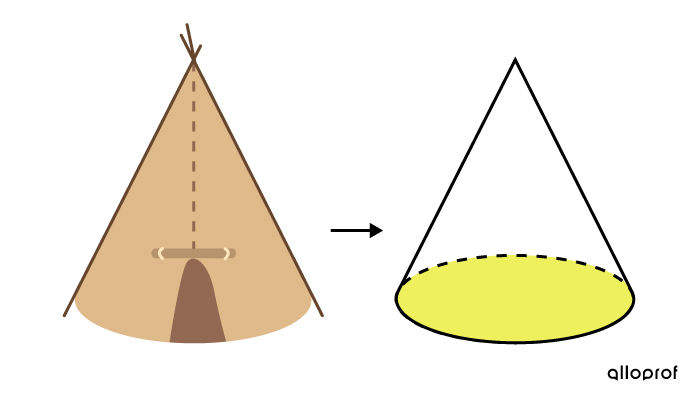
The carpet is placed on the floor. Therefore, the base of the cone is the focus and it is the only figure surface needed to solve the problem.
The Total Area
For a special occasion, we buy and wrap a gift for a loved one.
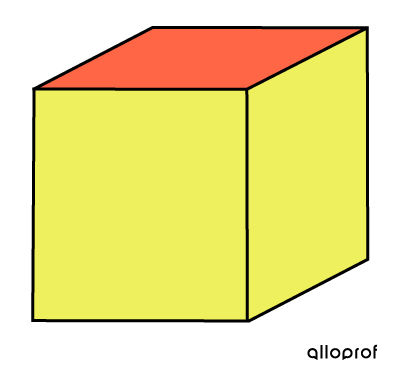
To wrap the solid, we must cover the 4 lateral faces as well as the 2 bases. Thus, the total area is needed to solve the problem.
In all cases, area is calculated in |\text{unit}^2| and the units of measurement used are, for example, |\text{cm}^2,| |\text{m}^2| or |\text{km}^2.| When the exponent 2 appears in the units, it means "squared": |\text{cm}^2| reads as "centimetres squared".
Sometimes, we must consider only one of the 2 bases or just part of the lateral faces. For more details, see the following concept sheets.
- Area of a Cube
- Area of Prisms
- Area of Pyramids
- Area of a Sphere
- Area of Cylinders
- Area of Cones
- Area of Decomposable Solids
- Area of Truncated Solids
- Finding the Area of a Solid Using Algebra
- Missing Measurements of Solids from the Area
- Missing Measurements According to Area: Decomposable and Truncated Solids
Volume of a Solid
The volume, generally denoted |V,| is the measure of the space a solid occupies.
To determine how many customers will receive their order, a gasoline distribution company needs to know how much gasoline its tanker truck can hold in |\text{m}^3.|
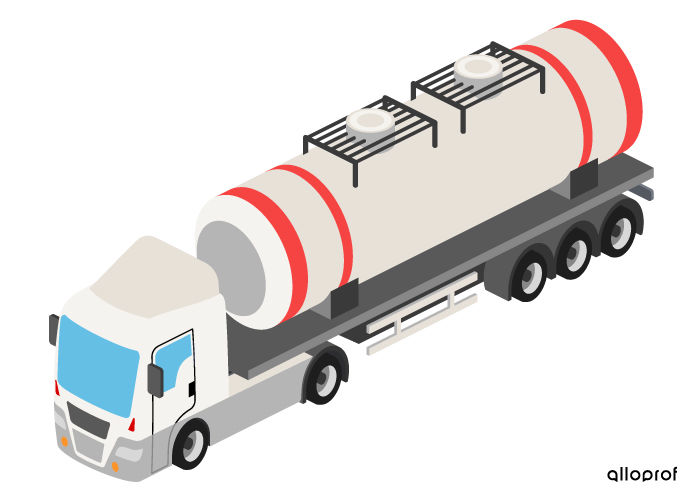
To fulfill their request, we must determine the 3D space occupied by the truck’s tank. Therefore, it is a volume question.
When we calculate volume, we can use two types of units. The first type uses metric units |(\text{cm}^3, \text{m}^3, \text{dam}^3, ...)| and is referred to as, for example, "cubic centimetres". The second uses capacity units |(\text{L}, \text{cl}, \text{ml}, ...).| To understand the relationship between the two, see the concept sheet on Units of Volume and their Conversion.
- Volume of a Cube
- Volume of Prisms
- Volume of Pyramids
- Volume of a Sphere
- Volume of Cylinders
- Volume of Cones
- Volume of Decomposable Solids
- Volume of Truncated Solids
- Volume of Solids Using Algebra
- Missing Measurements of Solids from the Volume
- Missing Measures from a Volume: Decomposable and Truncated Solids
Summary Table of the Formulas for the Area and Volume of Solids
The different formulas for solids are in the following table.
|
Solid |
Area Formulas |
Volume Formulas |
|---|---|---|
|
Cube  |
|\begin{align}A_b &= \ \color{#3a9a38}{s}^2\\\\ |
|
|
Prism  |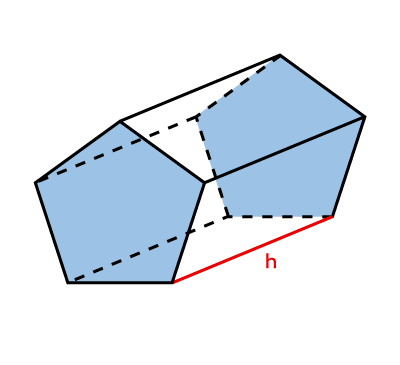
|\begin{align} \color{#3b87cd}{A_b} &= \text{formula associated with the figure} \\\\ |
|V = \color{#3b87cd}{A_b} \times \color{#ec0000}h| |
|
Pyramid  |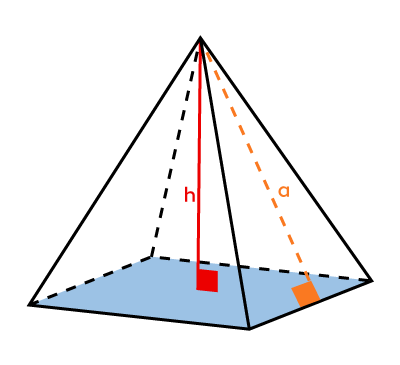
|\begin{align} \color{#3b87cd}{A_b} &= \text{formula associated with the figure} \\\\ |
|V = \dfrac{\color{#3b87cd}{A_b} \times \color{#ec0000}{h}}{3}| |
|
Sphere  |
|A_T = 4 \pi \color{#3a9a38}{r}^2| |
|V= \dfrac{4 \pi \color{#3a9a38}{r}^3}{3}| |
|
Cylinder  |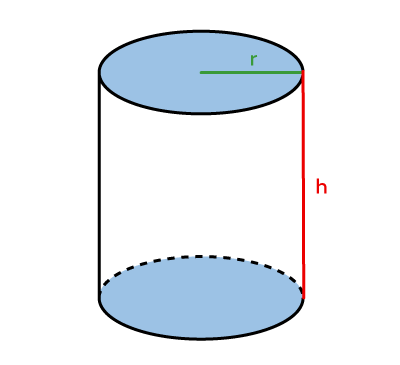
|\begin{align} |
|V = \color{#3b87cd}{A_b} \times \color{#ec0000}h| |
|
Cone  |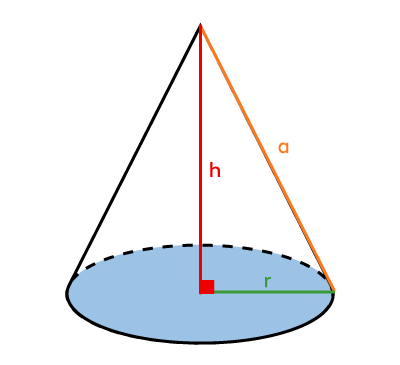
|\begin{align} \color{#3b87cd}{A_b} &= \pi \color{#3a9a38}r^2 \\\\ |
|V = \dfrac{\color{#3b87cd}{A_b} \times \color{#ec0000}h}{3}| |
The base(s) of prisms and pyramids can be different shapes. For help calculating their area, see the summary table of Area Formulas for Plane Figures.
To make sure you understand how to use the area and volume formulas of solids to find a missing measurement, check out the following interactive CrashLesson.
