Subjects
Grades
The Similarity Ratio for Lengths, Areas, and Volume (k, k², k³)
Concept sheet | Mathematics
When two plane figures are similar, there is a ratio of similarity between their corresponding sides (k) and their area (k²). When two solids are similar, there is a similarity ratio between their corresponding edges (k), their corresponding faces (k²) and their volume (k³).
Each of these ratios can be used to find a missing measurement in a figure or a missing measurement in a solid.
Table of contents
The ratios of similarity, area, and volume indicate either an enlargement or a reduction of the image figure with respect to the initial figure.
If the image figure is larger then the initial figure, then:||k=\dfrac{\color{#333fb1}{\text{Image Figure}}}{\color{#3a9a38}{\text{Initial Figure}}}=\dfrac{\color{#333fb1}{\text{Large Figure}}}{\color{#3a9a38}{\text{Small Figure}}}||where |k>1|
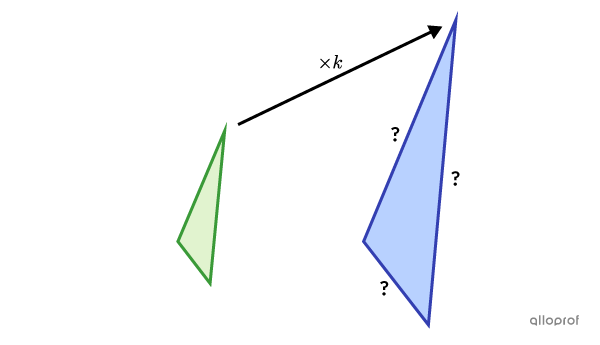
In this case, |k| is an enlargement ratio.
If the image figure is smaller then the initial figure, then:||k=\dfrac{\color{#333fb1}{\text{Image Figure}}}{\color{#3a9a38}{\text{Initial Figure}}}=\dfrac{\color{#333fb1}{\text{Small Figure}}}{\color{#3a9a38}{\text{Large Figure}}}||where |0<k<1|
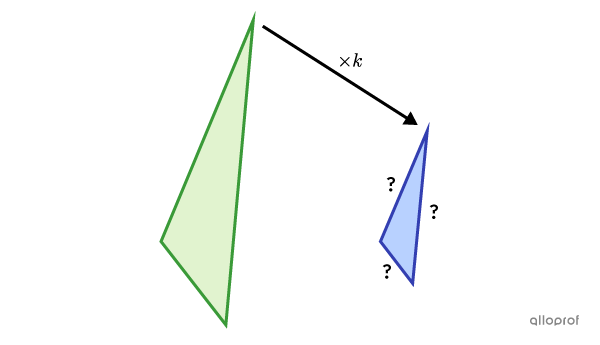
In this case, |k| is a reduction ratio.
Similarity, area, and volume ratios are only valid when comparing corresponding lengths, areas, or volumes. For example, the height of one pyramid with the apothem of another pyramid cannot be compared, because they are not corresponding segments.
Similarity Ratio (k)
The similarity ratio (or scale factor) (k) is the relationship between the corresponding lengths (i.e., sides, perimeters, radii, circumference, etc.) of two similar figures.
||k=\dfrac{\text{Length on the image figure}}{\text{Corresponding length on the initial figure}}||
Ratio of Areas (k²)
The ratio of areas |\boldsymbol{(k^2)}| is a ratio of the corresponding surfaces (areas of plane figures, bases of prisms, side faces of pyramids, etc.) of two similar figures.
||k^2=\dfrac{\text{Area of the image figure}}{\text{Area of the initial figure}}||
Ratio of Volumes (k³)
The ratio of volumes |\boldsymbol{(k^3)}| is a ratio of the volumes of two similar solids.
||k^3=\dfrac{\text{Volume of the image solid}}{\text{Volume of the initial solid}}||