Matières
Niveaux
Voici un petit guide de préparation contenant toutes les notions abordées en cinquième secondaire dans la séquence CST. Pour expliquer le tout, chaque formule sera suivie d'un exemple et d'un lien qui mène à une fiche sur notre site.
Forme fonctionnelle||y = ax + b||où
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}|
Forme générale||0 = Ax + By + C||où
|A, B, C \in \mathbb{Z}|
Avec les informations fournies dans le graphique ci-dessous, détermine l'équation de la droite sous sa forme générale.
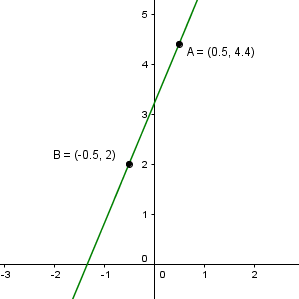
Pour résoudre un système d'équations par comparaison, on peut se fier aux étapes suivantes.
Identifier les variables reliées aux inconnus.
Créer les équations selon la mise en situation.
Isoler la même variable pour chacune des équations.
Comparer les 2 équations pour en former une nouvelle.
Résoudre cette nouvelle équation.
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
Pour résoudre une système d'équations par substitution, on peut se fier aux étapes suivantes.
Identifier les variables reliées aux inconnus.
Créer les équations selon la mise en situation.
Isoler une variable dans une des équations.
Substituer cette même variable dans l'autre équation par l'expression algébrique qui lui est associée.
Résoudre cette nouvelle équation.
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, des travailleurs achètent 4 cafés et 6 muffins pour 15,06 $. Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de 11,97 $. Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
Pour résoudre un système d'équation par réduction, on peut se fier aux étapes suivantes :
Identifier les variables reliées aux inconnus.
Créer les équations selon la mise en situation.
Trouver des équations équivalentes pour obtenir le même coefficient d'une même variable.
Soustraire les deux équations.
Isoler la variable restante pour trouver sa valeur.
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, des travailleurs achètent 4 cafés et 6 muffins pour 15,06 $. Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de 11,97 $. Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
Généralement, on pourra résoudre un problème d'optimisation en suivant les étapes suivantes.
Identifier les variables.
Traduire les contraintes de la situation par un système d'inéquations.
Établir la règle de la fonction à optimiser.
Tracer le polygone de contraintes.
Déterminer les coordonnées des sommets du polygone de contraintes.
Évaluer la fonction à optimiser en chaque sommet du polygone de contraintes.
Déduire le ou les sommets dont les coordonnées maximisent (ou minimisent) la fonction à optimiser et donner la réponse.
Afin de maximiser les profits de son entreprise, un directeur général tient à savoir combien de vestons et de chemises il doit vendre chaque semaine. À cause de certaines contraintes de production, il sait que le nombre maximal de chemises correspond au retranchement du quadruple de vestons à 21. À cause du transport, le nombre de vestons doit être plus grand ou égal à la différence entre 8 et le triple du nombre de chemises. Finalement, le reste entre le triple du nombre de vestons et le double du nombre de chemises doit être d'au moins deux.
En sachant que chaque veston vendu rapporte un profit de |32\ $| et que celui associé à la vente d'une chemise est de |17\ $,| quel est le profit maximal hebdomadaire qu'il peut espérer obtenir?
| TYPES D'ÉVÈNEMENTS | DÉFINITION | EXEMPLE |
|---|---|---|
| Mutuellement exclusifs | Lorsqu'ils ne peuvent pas se produire en même temps. | Lancer un dé à six faces et obtenir un résultat qui est à la fois un multiple de 3 et de 4. |
| Non mutuellement exclusifs | Lorsqu'ils peuvent se produire en même temps. | Piger une carte au hasard dans un jeu qui en contient 52 et en obtenir une qui est à la fois un as et de couleur rouge. |
| Dépendants | Lorsque la réalisation de l'un affecte la réalisation de l'autre. | Piger successivement et sans remise deux cartes dans un paquet qui en contient 52 au départ. |
| Indépendants | Lorsque la réalisation de l'un n'influe pas sur la réalisation de l'autre. | Piger une carte dans un paquet qui en contient 52 et lancer un dé à six faces. |
Il ne faut pas oublier les types d'événements qui ont été vus dans les années précédentes (certaines, probables, impossibles, élémentaires, complémentaires, compatibles et incompatibles).
Soit |a = | les chances pour et |b =| les chances contre, alors :
Le rapport des chances pour |\displaystyle = a : b \Rightarrow \frac {a}{a+b}|
Le rapport des chances contre |\displaystyle = b : a \Rightarrow \frac {b}{b+a}|
Ainsi, on obtient le gain net selon la proportion suivante : ||\displaystyle \frac{\text{Montant de la mise}}{\text{Gain net}} = \frac{\text{nb de chances sur lequelles on mise}}{\text{nb total de chances}}||
À l'époque de l'hippodrome de Québec, on pouvait parier sur les victoires des chevaux de course. Ainsi, chaque cheval possédait une cote qui quantifiait ses chances de gagner. Pour la dernière course, un amateur a parié |20\ $| pour la victoire dont la cote était |1:14.| Ainsi, quel était le gain potentiel de son pari?
Pour certains combats de boxe, on peut parier sur la défaite d'un boxeur. Ainsi, chaque pugiliste possède une cote qui quantifie ses chances de gagner. Pour le prochain combat, le champion a une cote de |44 : 1| pour sa victoire. Ainsi, quel serait le gain net d'un amateur qui parierait |10\ $| contre une victoire du champion?
||\mathbb{E} = (p_1 x_1 + p_2 x_2 + ... + p_i x_i) - M||où
|p_i = | probabilité de réalisation de l'évènement |i|
|x_i =| montant associé à l'évènement |i|
|M =| montant de la mise initiale
Dans le but de financer l'équipe de ski acrobatique de l'école, des organisateurs mettent sur un pied une activité de financement pour laquelle il est possible de gagner les prix de participations suivants.
un forfait de ski familial d'une fin de semaine (valeur de 800 $);
deux billets de saison de ski alpin (valeur de 500 $ chacun);
quatre paires de ski (valeur de 300 $ chacune);
huit billets de remontée valide pour une journée (valeur de 45 $ chacun).
Sachant qu'ils ont un total de 336 billets à vendre, quel devrait être le prix de vente d'un billet de participation au tirage?
Si |\mathbb{E} = 0|, alors le jeu est équitable.
Si |\mathbb{E} < 0|, alors le jeu est défavorable au joueur.
Si |\mathbb{E} >0|, alors le jeu est favorable au joueur.
||P(A \mid B) =\dfrac{P (A \cap B)}{P (B)}||où||P(A) >0||
Au cours du mois précédent, les auditeurs et auditrices d'une chaine de radio québécoise avaient la chance de gagner un voyage au domaine féérique de Walt Disney. Avant de faire le tirage du gagnant ou de la gagnante au hasard, le radiodiffuseur a dressé le portrait global des participants et participantes.
Quelle est la probabilité que le gagnant soit père d'une famille de trois enfants et qu'il se soit fait donner le billet de tirage en cadeau?
À voir aussi
Deux figures sont équivalentes lorsqu'elles ont la même aire.
Afin que le cout d'asphaltage de son nouveau stationnement résidentiel soit le même que celui de son ancien, Julien veut que ses deux entrées soient équivalentes.
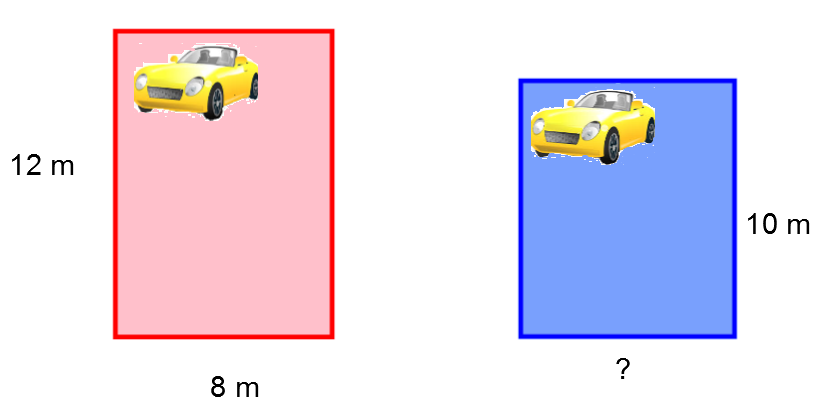
Ainsi, quelle devrait être la mesure de la largeur de son nouveau stationnement?
Deux solides sont équivalents lorsqu'ils ont le même volume.
Une compagnie qui œuvre dans les accessoires de plein air veut offrir deux modèles de tente différents. Afin de conserver les mêmes couts de production, la compagnie tient à ce que ces deux modèles soient équivalents.
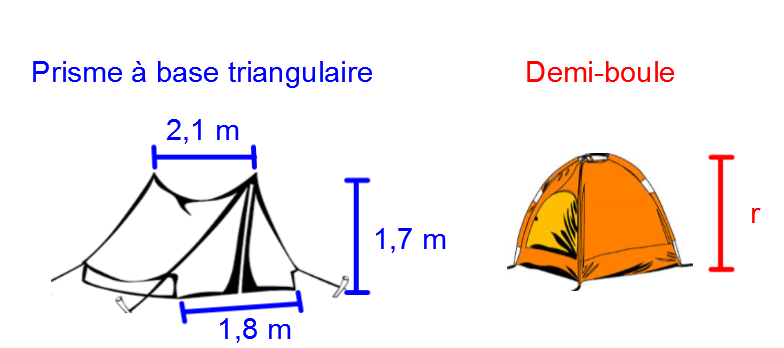
Quelle devrait être la mesure de la hauteur du second modèle afin de respecter la condition de similitude?
Pour tout |\{a,b\} \in \mathbb{R}| et |\{m,n\} \in \mathbb{N}|, on déduit les propriétés suivantes.
Si |a^m = a^n,| alors |m = n.|
|a^m \times a^n = a^{m+n}|
|\dfrac{a^m}{a^n} = a^{m-n}| où |a \neq 0|
|(ab)^m = a^mb^m|
Résous l'équation suivante. ||6 \ 300 (1{,}2)^{3x} = 175 (7{,}2)^2||
Pour les propriétés suivantes, il est important de considérer que |\{m\} \in \mathbb{R}_+ \ \ \text{et} \ \ \{c,n\} \in \mathbb{R}|.
|\log_c 1 = 0|
|\log_c c = 1|
|\log_c m^n = n\log_c m|
|\log_c (mn) = \log_c m + \log_c n|
|\log_c \left(\dfrac{m}{n}\right) = \log_c m - \log_c n|
|\log_c m = \dfrac{\log_a m}{\log_a c}|
Résolution d'une équation exponentielle
Quelle est la valeur de |x| dans l'équation |4\ 500 = 1\ 500 (1{,}08)^{^{\large{\frac{x}{2}}}}?|
||\begin{align} \dfrac{4\ 500}{\color{red}{1\ 500}} &= \dfrac{1\ 500}{\color{red}{1\ 500}} (1{,}08)^{^{\large{\frac{x}{2}}}} && \text{Opération inverse} \\\\ 3 &= (1{,}08)^{^{\large{\frac{x}{2}}}} \\\\ \log_{1{,}08} 3 &= \dfrac{x}{2} && \text{Déf. du log} \\\\ \dfrac{\log_{10} 3}{\log_{10} 1{,}08} &= \dfrac{x}{2} &&\text{Changement de base} \\\\ 14{,}275\ \color{red}{\times 2} &\approx \dfrac{x}{2}\ \color{red}{\times 2} && \text{Opération inverse} \\\\ 28{,}55 &\approx x \end{align}||
Résolution d'une équation logarithmique
Quelle est la valeur de |x| dans l'équation |\log_5 x^3 + \log_5 \ \left(\dfrac{x}{32}\right) = \log_5 \ 732 - 1?|
||\begin{align} \log_5 x^3 + \log_5 \left(\dfrac{x}{32}\right) &= \log_5 732 - 1 \\\\ 3 \log_5 x + \log_5 \left(\dfrac{x}{32}\right) &= \log_5 732 - 1 && \text{Puissance d'un log}\\\\ 3 \log_5 x + (\log_5 x - \log_5 32) &= \log_5 732 - 1 && \text{Log d'un quotient} \\\\ 3 \log_5 x + \log _5 x - 2{,}153 &\approx 4{,}098 - 1 && \text{Loi du changement de base} \\\\ 4 \log_ 5 x - 2{,}153 &\approx 4{,}098 - 1 && \text{Termes semblables} \\\\ 4 \log_5 x - 2{,}153 \color{red}{+2{,}153} &\approx 4{,}098 - 1 \color{red}{+ 2{,}153} && \text{Opération inverse} \\\\ \dfrac{4 \log_5 x}{\color{red}{4}} &\approx \dfrac{5{,}251}{\color{red}{4}} && \text{Opération inverse} \\\\ \log_5 x \approx 1{,}313 &\Rightarrow 5^{1{,}313} = x && \text{Déf. du log} \\\\ 8{,}275 &\approx x \end{align}||
||\begin{align}
C_0&=C_n\left(1+\dfrac{i}{k}\right)^{-x}\\\\
C_0&=\dfrac{C_n}{\left(1+\dfrac{i}{k}\right)^x}\\\\
\end{align}||
où
||\begin{align}
C_0&:\text{valeur actuelle}\\
C_n&:\text{valeur future}\\
i&:\text{taux d'intérêt annuel en notation décimale}\\
k&:\text{facteur en lien avec la période d'intérêt}\\
x&:\text{nombre de périodes d'intérêt}
\end{align}||
Pour s'assurer d'une retraite des plus agréables, Christian doit obtenir une valeur future de |200\ 000\ $| sur un placement qu'il fait aujourd'hui. Ainsi, quel devrait être la valeur actuelle de son placement s'il sait qu'il sera soumis à un taux d'intérêt annuel de |2{,}59\ \%| composé mensuellement sur une période de |35| ans?
Cette procédure confère la victoire à l'individu ou au groupe qui obtient la majorité des votes, soit |50\ \%+1| du nombre total de votes représentant une majorité absolue.
Aux dernières élections fédérales canadiennes, les différents partis avaient pour but de faire élire le plus de députés et députées possible parmi les 338 circonscriptions du pays. Après la compilation des résultats, voici la répartition du pouvoir.
|
Parti politique |
Nombre de député(e)s élu(e)s |
|---|---|
|
Parti Conservateur |
|125| |
|
Parti Vert |
|4| |
|
Parti Libéral |
|171| |
|
Nouveau Parti Démocratique |
|16| |
|
Bloc Québécois |
|22| |
Cette procédure confère la victoire à l'individu ou au groupe qui obtient le plus grand nombre de votes, soit la majorité absolue.
Pour élire le nouveau capitaine de l'équipe de hockey des Canadiens de Montréal, le directeur général a demandé l'opinion de tous les joueurs qui ont un contrat avec l'équipe. Ainsi, chacun d'entre eux devait inscrire le nom du joueur qu'il désirait avoir comme leadeur de l'équipe. Voici les résultats qui ont été compilés par la direction.
|
Joueur |
Nombre de votes |
|---|---|
|
Brendan Gallagher |
2 |
|
P.K. Subban |
1 |
|
Max Pacioretty |
16 |
|
David Desharnais |
5 |
|
Tomas Plekanec |
1 |
|
Andrei Markov |
11 |
En s'appuyant sur la méthode de la pluralité, qui sera nommé capitaine de cette équipe?
Cette procédure confère la victoire à l'individu ou au groupe qui obtient le plus de points en accordant |n-1| points pour le 1er choix de chaque électeur ou électrice, |n-2| points pour le 2e choix et ainsi de suite pour les |n| candidats.
Pour être intronisés au Temple de la Renommée du Hockey, les joueurs en nomination sont classés par ordre de préférence par les membres du comité du Temple. Afin d'alléger la présentation des résultats, les votes présentant des préférences identiques ont été regroupés. Voici la liste de quatre joueurs ainsi que leur classement de préférence en 2014.
|
Choix |
7 membres |
6 membres |
4 membres |
|---|---|---|---|
|
1er choix |
Dominik |
Mike |
Peter |
|
2e choix |
Peter |
Peter |
Rob |
|
3e choix |
Mike |
Dominik |
Mike |
|
4e choix |
Rob |
Rob |
Dominik |
En utilisant la méthode de Borda, quel serait le prochain joueur à être intronisé au Temple de la Renommée du Hockey?
Cette procédure confère la victoire à l'individu ou au groupe qui remporte tous ses duels en face-à-face selon les préférences des électeurs- et des électrices.
Si aucun individu ou groupe ne remporte tous ses duels, il est préférable d'utiliser une autre procédure.
Pour être intronisés au Temple de la Renommée du Hockey, les joueurs en nomination sont classés par ordre de préférence par les membres du comité du Temple. Afin d'alléger la présentation des résultats, les votes présentant des préférences identiques ont été regroupés. Voici la liste de quatre joueurs ainsi que leur classement de préférence en 2014.
|
Choix |
7 membres |
6 membres |
4 membres |
|---|---|---|---|
|
1er choix |
Dominik |
Mike |
Peter |
|
2e choix |
Peter |
Peter |
Rob |
|
3e choix |
Mike |
Dominik |
Mike |
|
4e choix |
Rob |
Rob |
Dominik |
En utilisant le principe de Condorcet, quel serait le prochain joueur à être intronisé au Temple de la Renommée du Hockey?
Cette procédure confère la victoire à l'individu ou au groupe qui obtient le plus grand nombre de votes alors que les électeurs et électrices peuvent voter une seule fois, mais pour autant de candidats et candidates qu'ils le veulent.
Afin d'éviter le vote populaire, le vote par assentiment est utilisé pour élire le prochain président ou la prochaine présidente de classe. Suite au dépouillement des résultats, on obtient le tableau suivant.
|
Nombre d'électeur(-trice)s qui ont voté |
5 |
8 |
10 |
7 |
3 |
|---|---|---|---|---|---|
|
|
Marie-Claude |
Simon |
Vincent |
Judith |
Simon |
|
|
Gitane |
Vincent |
Gitane |
Marie-Claude |
Judith |
|
|
|
Gitane |
Simon |
Vincent |
En compilant les résultats de façon adéquate, qui serait le gagnant ou la gagnante de cette élection en suivant le principe de vote par assentiment?
Cette procédure confère la victoire à l'individu ou au groupe qui obtient la majorité des votes, soit |50\ \%+1| du nombre total de votes, alors que les électeurs et les électrices les classent selon un ordre de préférence. S'il n'y a pas de majorité absolue dès le premier comptage, on élimine le moins populaire pour transférer ses votes au candidat ou à la candidate qui le suit.
Pour être intronisés au Temple de la Renommée du Hockey, les joueurs en nomination sont classés par ordre de préférence par les membres du comité du Temple. Afin d'alléger la présentation des résultats, les votes présentant des préférences identiques ont été regroupés. Voici la liste de quatre joueurs ainsi que leur classement de préférence en 2014.
|
Choix |
7 membres |
6 membres |
4 membres |
|---|---|---|---|
|
1er choix |
Dominik |
Mike |
Peter |
|
2e choix |
Peter |
Peter |
Dominik |
|
3e choix |
Mike |
Dominik |
Mike |
En utilisant la méthode de vote par élimination, quel serait le prochain joueur à être intronisé au Temple de la Renommée du Hockey?
Pour bien comprendre les notions de cette section, il est important de maitriser le vocabulaire suivant.
Sommets : les différents éléments qui sont mis en relation (personnes, étapes à suivre, etc.) et qui sont généralement représentés par des points.
Arêtes : les liens qui mettent en relation les éléments et qui sont généralement représentés par des lignes ou des arcs de cercles.
Arêtes parallèles : lorsque deux arêtes ont les mêmes sommets de départ et d'arrivée.
Boucle : arête qui débute et se termine avec le même sommet.
Degré : le nombre de fois qu'un sommet est touché par les différentes arêtes.
Chaine : une suite d'arêtes que l'on emprunte pour se « promener » sur le graphe.
Longueur : correspond au nombre d'arêtes empruntées dans une chaine.
Distance : nombre d'arrête minimal pour passer du sommet de départ au sommet d'arrivée.
Chaine simple : une chaine dont chacune des arêtes est empruntée une seule fois.
Cycle : une chaine qui débute et se termine au même sommet.
Cycle simple : un cycle dans lequel chaque arête est utilisée une seule fois.
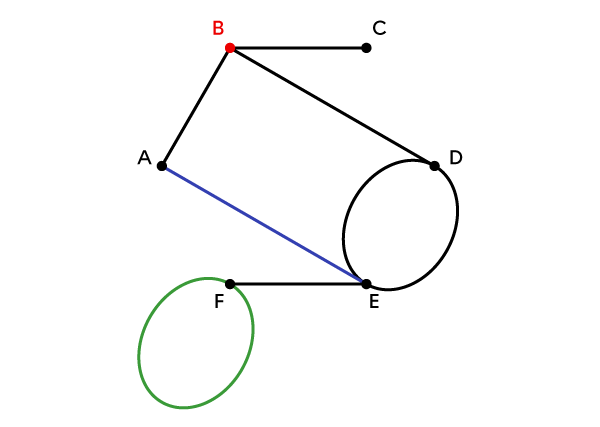
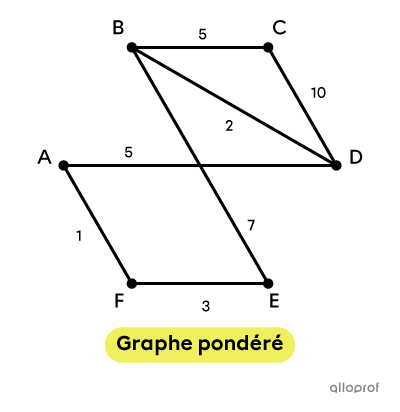
|\color{#ec0000}{B}| est un sommet.
|\color{#333fb1}{A — E}| est une arête.
|\color{#3a9a38}{F — F}| est une boucle.
|E — D| et |D — E| sont des arêtes parallèles.
Le degré de |\color{#ec0000}{B}| est |3.|
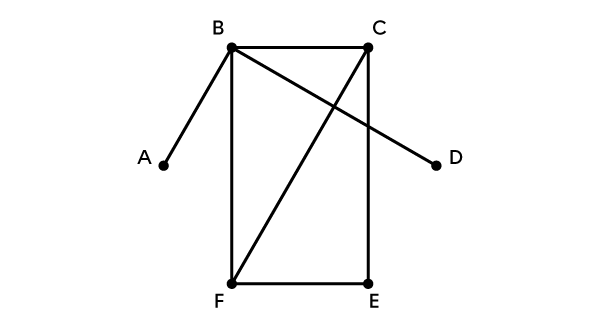
|\color{#ec0000}{B-F-E-C-F-B}| est un cycle.
|\color{#3a9a38}{D-B-C-B-A}| est une chaine.

|\color{#3a9a38}{A-B-C-F}| est une chaine simple de longueur |3,| mais la distance |\color{#333fb1}{d(A,F)=2}.|
Finalement, |\color{#3a9a38}{A-B-C-F}\color{#333fb1}{-E-A}| est un cycle simple de longueur |5.|
La caractéristique eulérienne d'un graphe exige que toutes les arêtes soient impliquées une seule fois dans la chaine ou le cycle.
En tant que policier ou policière, tu veux connaitre les moindres recoins de la région que tu dois desservir. Pour ce faire, tu décides de patrouiller dans chacune des rues de ton district durant ton quart de travail. Pour t'aider, tu utilises une carte routière pour identifier le territoire que tu as à superviser.
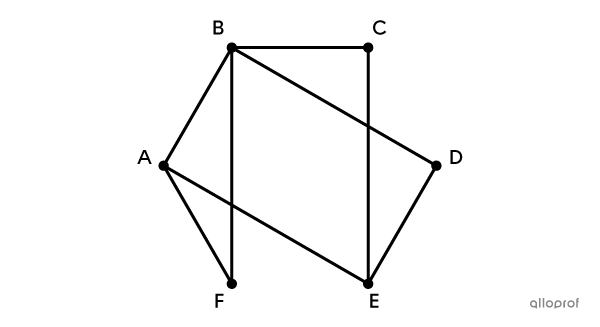
En gardant en tête que tu peux décider du point de départ et d'arrivée de ton itinéraire, quelle séquence de routes devrais-tu emprunter pour patrouiller dans chacune des rues, et ce, le plus efficacement possible?
La caractéristique hamiltonienne d'un graphe exige que tous les sommets soient impliqués une seule fois dans la chaine ou le cycle.
Pour compléter un rallye automobile, les concurrents et les concurrentes doivent obligatoirement passer par chacune des bornes identifiées par des lettres sur la carte suivante.
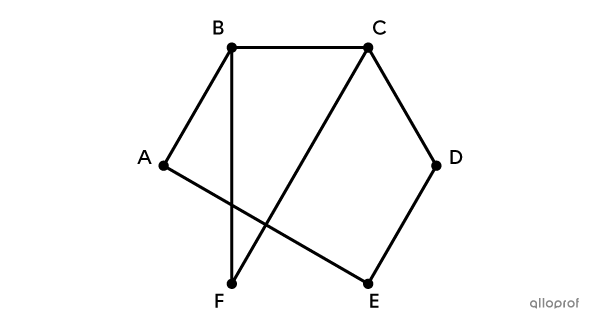
En gardant à l'esprit qu'ils doivent revenir au point de départ identifié par le sommet |A| pour terminer la course, quelle pourrait être une des routes empruntées par les concurrent(e)s?
En fonction des informations qui sont fournies sur le graphe, il est possible de lui associer un nom bien précis.
Connexe : lorsque tous les sommets sont accessibles à partir de n'importe quel sommet.
Arbre : se dit d'un graphe qui ne possède aucun cycle simple.
Orienté : lorsque les arêtes suggèrent, par le biais d'une flèche, une orientation précise.
Pondéré (valué) : lorsque chacune des arêtes ont une quantité qui leur est associée.
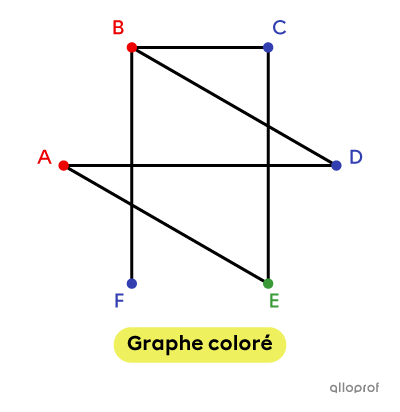
Coloré : Lorsque les sommets sont associés à des couleurs particulières.
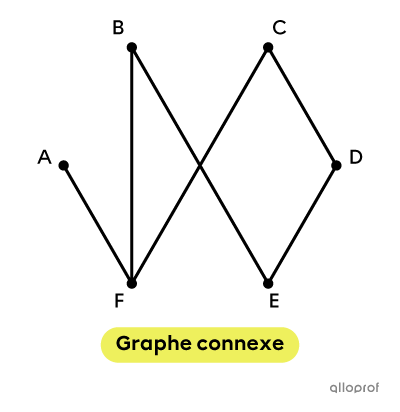



Concrètement, le chemin critique est souvent utilisé pour établir une échéance de réalisation pour un projet.
Avant d'acheter une maison, il est important de bien analyser divers éléments qui vont permettre d'effectuer un achat judicieux. Afin de ne rien oublier dans le processus, voici quelques pistes.
|
Tâches |
Temps (jours) |
Préalables |
|---|---|---|
|
A : Établir ses besoins |
1 |
Aucun |
|
B : Établir un budget |
5 |
A |
|
C : Magasiner une hypothèque |
7 |
B |
|
D : Engager un ou une notaire |
3 |
B |
|
E : Engager un ou une agent(e) immobilier(-ère) |
3 |
B |
|
F : Visiter des maisons |
182 |
C - D - E |
|
G : Négocier un taux d’intérêt |
7 |
F |
|
H : Obtenir une pré-autorisation de prêt |
30 |
F |
|
I : Faire une offre |
7 |
G - H |
|
J : Faire inspecter la maison |
14 |
I |
|
K : Signer l’acte de vente |
2 |
J |
|
L : Contracter une assurance habitation |
10 |
J |
|
M : Déménager |
1 |
K - L |
Quelle est la durée totale d'un tel projet?
Concrètement, le nombre chromatique est souvent utilisé pour colorier une carte mondiale, concevoir des puces électroniques ou planifier un réseau de télécommunication.
Voulant apprendre à connaitre ses collègues au maximum, Mme Dreau veut participer à un maximum d'activités offertes par son école. Par contre, certaines contraintes dans son horaire l'empêchent de participer à tout ce qu'elle voudrait.
le journalisme entre en conflit avec quelques séances d'improvisation et de soutien à la réussite;
il lui est impossible de s'inscrire au basketball, au théâtre et à la danse en même temps;
le soutien à la réussite et le théâtre sont tous deux à l'horaire du lundi soir.
Quel est le nombre maximal d'activités auxquelles elle pourra participer?
Concrètement, l’arbre de valeurs est souvent utilisé pour minimiser ou maximiser des couts ou des distances.
Avant d'entamer la construction de résidences dans un nouveau quartier, une ville doit installer un réseau d'aqueduc et d'égout qui relie chacune des résidences. Malgré quelques contraintes géographiques, la majorité des maisons peuvent être reliées par ce futur système.
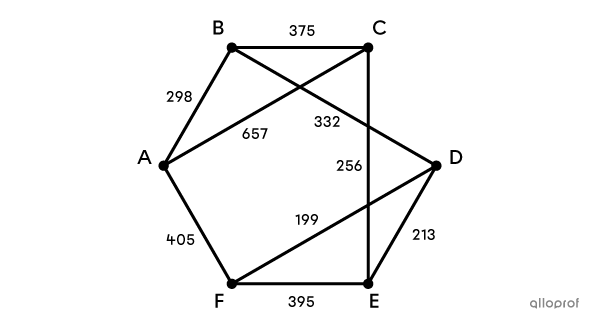
En considérant les quantités du graphe comme étant la distance, en mètres, entre chacune des maisons, quelle serait la longueur minimale du réseau de ce quartier?